Types and Operations
-- 打开一些扩展
{-# EmptyDataDecls, TypeOperators #-}
One
Unit 是类型中的单位元,对应着 1。
data Unit = Unit -- 左边是类型,右边是它的 constructor
-- data () = ()
Addition
Sum 类型对应了加法。
data a :+ b = AddL a | AddR b
-- data Either a b = Left a | Right b
Multiplication
元组对应乘积。
data a :* b = Mul a b
-- data (a, b) = (a, b)
Zero
data Void -- No construction
Void 没有 constructor 意味着不存在对应的 value。
Two
type Two = Unit :+ Unit
-- data Bool = False | True
Laws
如果两个类型可以一一对应(双射),那么就认为两个类型相等,即可以将一个类型映射到另一个类型上。
\(0 + x = x\)
\[ \operatorname{\mathtt{Either}}\ \operatorname{\mathtt{Void}}\ x \cong x \]
因为 Void 没有 Value,因此对于 Either Void x 来说其类型一定是 x。
\(0 * x = 0\)
\[ (\operatorname{\mathtt{Void}}, x) \cong \operatorname{\mathtt{Void}} \]
同理,Void 的值不能构造,其元组一定也不存在。
\(1 * x = x\)
\[ ((), x) \cong x \]
一个已经确定了,只有 x 不知道。
\(x + y = y + x\)
\[ \operatorname{\mathtt{Either}}\ x\ y \cong \operatorname{\mathtt{Either}}\ y\ x \]
\(x * y = y * x\)
\[ (x, y) \cong (y, x) \]
类型与自然数
通过上面的例子可以发现 \(\langle T, +, * \rangle\) 构成了一个交换半环(可交换,没有加法逆元的环)。
*的单位元是Unit,因为Unit * T = T * Unit = T;+的单位元是Void,因为Void + T = T + Void = Void;- 不难发现这也满足分配率:
T1*(T2 + T3) = T1*T2 + T1*T3。
定义函数 f(T) 表示类型 T 包含值的数量,那么就可以将类型映射到自然数上。即 \(f\) 是 \(\langle T, +, * \rangle\) 到 \(\langle N, +, *\rangle\) 的同态映射。其中 Unit 映射到 1,Void 映射到 0。
Function
data a -> b
函数类型比较特殊,考虑前面提到的等价方式,类型 a 有 f(a) 个值,b 有 f(b) 个值。则从类型 a 到 b 的(全)函数类型表示 a 到 b 的映射中不相同的映射方式的数量。
对于 a 的第一个元素,有 f(b) 种映射方式,对于第二个元素也有 f(b) 种映射方式……因此全体 a 类型,共有 \(f(b) * f(b) * \cdots * f(b) = f(a)^{f(b)}\)。
因此 \(a \rightarrow b \cong b^a\)。
Laws
\(1^a = 1\)
\[ a \rightarrow () \cong () \]
\(a^1 = a\)
\[ () \rightarrow a \cong a \]
\((b c)^a = b^a c^a\)
\[ a \rightarrow (b, c) \cong (a \rightarrow b, a \rightarrow c) \]
\(c^{b a} = (c^b)^a\)
\[ (a, b) \rightarrow c \cong a \rightarrow b \rightarrow c \]
这条规则恰好对应了 Curry-ing。
Recursive Types
Lists
data List x = Nil | Cons x (List x)
仿照上面的方式将这个类型定义改写成代数方程,其中 L(x) 是一个 type constructor。
\[ L(x) = 1 + x * L(x) \]
对这个方程进行求解得到
\[ L = \frac{1}{1 - x} \]
这个式子有倒数,看不出其本质,下面将其展开成多项式:
\[ L = 1 + x + x^2 + x^3 + \cdots = \sum x^i \]
将其还原成类型即可以得到 Lists 的原始定义。
\[ L \cong () \quad | \quad x \quad | \quad (x, x) \quad | \quad (x, x, x) \quad | \quad \cdots \]
也就是说一个 Lists 类型是由上面这些东西组成的。
其实也可以用另一种方式得到这个同构关系:
\[ L = 1 + x (1 + xL) = 1 + x + x^2 (1 + xL) + 1 + x + x^2 + x^3 (1 + xL) + \cdots \]
Binary Trees
data Tree x = Tip | Node (Tree x) x (Tree x)
同理,将其转换成代数方程并求解、展开:
\[ T(x) = 1 + T(x) \times x \times T(x) = 1 + x T(x)^2 \]
\[ T = \frac{1 - \sqrt{1 - 4x}}{2x} = 1 + x + 2 x^2 + 5x^3 + \cdots \]
这个东西也反映了 Tree 的构成。例如 \(5 x^3\) 表示 3 个结点的二叉树共有 5 种不同的形式(这里又联系到了生成函数):
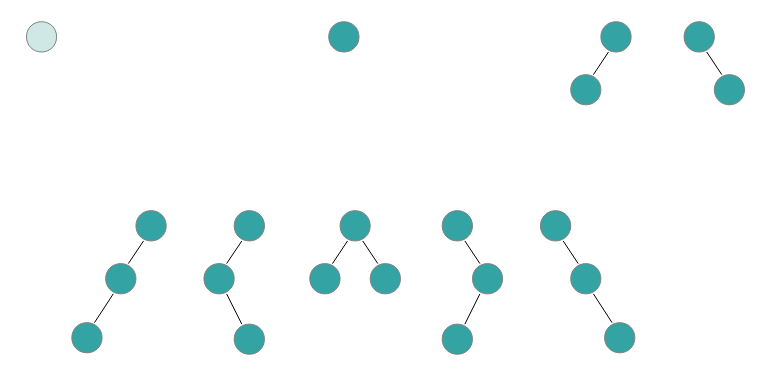
Figure 1: Binary Trees
如果这里令 x 表示具体的类型(例如令 x = Bool 表示 2),带入具体的数值,就可以表示特定类型的 List 具体的组成元素(相当于每个结点有 x 种可能)。
One-Hole Contexts
Structures with a HOLE
Zippers
Zippers 是 Haskell 里面用于遍历数据结构的结构,它有一个指向一个位置的指针,并且可以前后移动。
data Zip a = Zip [a] a [a]
let x = [1, 2, 3, 4, 5, 6]
let z = Zip [2, 1] 3 [4, 5, 6]
right z -- Zip [3, 2, 1] 4 [5, 6]
One-Hole Contexts
Zippers 相当于给数据结构挖了一个“孔”,并得到了一个 pair:[3, 2, 1] * [5, 6]。后者则是其 One-Hole Contexts。
类似的,可以构造其他类型的 One-Hole Contexts,并同构到代数表达式上:
- \(x \cong x \Longrightarrow () \cong 1\):
x里面只能挖掉x,此时只剩下() - \((x, x) \cong x^2 \Longrightarrow (*, x) + (x, *) \cong 2x\):可以挖掉左边或者右边的
x - \((x, x, x) \cong x^3 \Longrightarrow (*, x, x) + (x, *, x) + (x, x, *) \cong 3x^2\)
类型求导
不难发现,挖掉一个孔后得到类型所对应的代数表达式恰好是原表达式求导的结果!
The Derivative of a Regular Type is its Type of One-Hole Contexts – Conor McBride
由此可以得到一系列运算法则:
\[ \partial (f + g) = \partial f + \partial g \]
\[ \partial (f * g) = \partial f * g + f * \partial g \]
\[ \partial f(g) = \partial f(g) * \partial g \]
其中最后一个法则表示 type constructor 的嵌套,例如 List(List(x))。
由此可以给其他类型也进行求导。
对 Lists 求导
\begin{aligned} L &= \frac{1}{(1 - x)} \\ \partial L &= \frac{1}{(1 - x)^2} = L^2 \cong (L, L) \end{aligned}
可以发现求导后得到的类型就是 Zipper。
对 Binary Trees 求导
\begin{aligned} T &= 1 + x T^2 \\ \partial T &= T^2 + 2 x T \partial T \\ \Rightarrow \partial T &= \frac{T^2}{1 - 2 x T} = T^2 * L(2xT) \end{aligned}
对二叉树的方程求偏导后得到其表达式,此时会发现这里面的 \(\frac{1}{1 - x}\) 就是 Lists,因此将其带入得到最后的表达式。
这个表达式的含义是什么?如图。
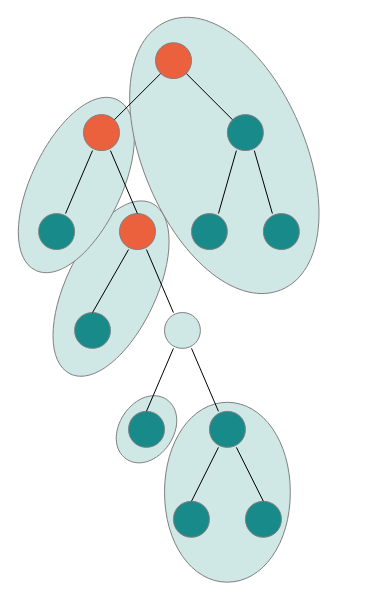
Figure 2: One-Hole Contexts of Trees
在这个图中挖掉一个点,可以得到其左右子树(对应了 \(T^2\))以及一条这个点到根节点的路径(对应 \(L\))。其中,路径上的每个点都还剩下一棵子树,加上其本身即为 \(xT\)。又因为子树可能是左子树或右子树,则其类型应该是 \(xT + xT\),即 \(2xT\)。最终得到了一个 pair:\(T^2 L(2xT)\)。
Regular Type
一个 Regular Type 必须是偏序的,并且允许存在重复元素。
- Bags: No ordering
- ULists: Unique elements
- Sets: No ordering & Unique elements
- Cyclic lists, dequeues…: No Ordering
上面这些数据类型就不是 Regular Types,所以不能将他们简单映射到代数。但是他们在代数中也可以有 interpretations。下面以 Set 为例。
Set in Algebra
Define \(\operatorname{\mathtt{Set}}_n = \text{“Sets of size n”}\)
\begin{aligned} \operatorname{\mathtt{Set}}_0(x) &\cong 1 &&\text{ - - empty set} \\ \operatorname{\mathtt{Set}}_1(x) &\cong x &&\text{ - - have one value} \\ \operatorname{\mathtt{Set}}_2(x) &\cong \frac{x (x-1)}{2} &&\text{ - - set with two values} \\ \operatorname{\mathtt{Set}}_n(x) &\cong \frac{x (x-1) \cdots (x-n+1)}{x!} = \frac{x^{\underline{n}}}{n!} \end{aligned}
这里需要一点组合数学:值得注意的是 Set 是无序的,所以要除以 \(n!\);同时由于不存在重复元素,所有是 \(x^{\underline{n}}\)。
由此可以得到:
\[ \operatorname{\mathtt{Set}}(x) = \sum \operatorname{\mathtt{Set}}_i(x) \cong 1 + x + \frac{x^{\underline{2}}}{2!} + \frac{x^{\underline{3}}}{3!} + \cdots \]
下面利用差分 \(\Delta f(x) = f(x + 1) - f(x)\) 化简这个式子:
\[ \operatorname{\mathtt{Set}}(x+1) - \operatorname{\mathtt{Set}}(x) = \Delta \operatorname{\mathtt{Set}}(x) = \operatorname{\mathtt{Set}}(x) \]
\[ \operatorname{\mathtt{Set}}(x+1) = 2 \operatorname{\mathtt{Set}}(x) \]
所以可以得到
\[ \operatorname{\mathtt{Set}}(x) \cong 2^x \]
这意味着:
\[ \operatorname{\mathtt{Set}} x \cong x \rightarrow \operatorname{\mathtt{Bool}} \]
Reference
- The Derivative of a Regular Type is its Type of One-Hole Contexts
- Combinatorial Species (Andre Joyal, Brent Yorgey)
- Calculus of Types (Conor McBride, Dan Piponi)