(incr j) 与 (add1 j)
想要将一个数字加一有两种写法:
(claim incr
(→ Nat
Nat))
(define incr
(λ (n)
(iter-Nat n
1
(+ 1))))
(+ 1)
; normal form 为 (λ (j) (add1 j))
=-表达式
Sameness 是一种表达二者相等的 judgment,而“相等”可以写成一个 type = 来表达 sameness(自反性)。
(The Law of
=)An expression
(= X from to)is a type ifXis a type,fromis anX, andtois anX.注解:这里只要求
from和to都是X,而不要求它们两个相等才算一个 type。比如(= Nat 0 1)也是一个 type,尽管它们实际上不等。
C-H 同构
=-表达式的意义是什么?
我们要用一种全新的视角来看待 type,即将它们看作一种 statements(或者叫 propositions)。
=-expression
- Statement: Three plus four equals seven
- Expression:
(= Nat (+ 3 4) 7) - Judgment:
(+ 3 4)is a judgment about expression(注意 Judgment 的四种形式)
Π-expression
Statement: For every Nat
n,(+ 1 n)equals(add1 n)Expression:
(Π ((n Nat)) (= Nat (+ 1 n) (add1 n)))
Types as Statements
如果一个 statement 为真,那么它有一个“对应类型的 expression”。
(+ n 0)andnare equal NatsThe expression with type
(= Nat (+ n 0) n)
证明
命题为真意味着我们有证据(evidence),这种 evidence 即证明(proof)。
Value as Proof
看待 statements 时,可以将其看作需要被证明的问题。所以前面声明类型时我们用 claim 这个关键字,claim 意味着需要一个 definition。
前面讲了 =-表达式什么时候能成为 type,但是没有指出这种 type 对应的 value(即 proof)应该是什么。
same: proof of =
= 对应的 constructor 只有一个,即 same。same 需要一个参数 e。
(The Law of
same)The expression
(same e)is an(= X e e)ifeis anX.
例如 (same (incr 3)) is an (= Nat (+ 2 2) 4)。前者是后者的 proof。
在 same 中要求 the from is the same X as the to。
通过 = 和 same,现在可以用 expressions 来描述一个 judgment,这个过程称为 internalizing the form of judgment。
证明:+1=add1
(claim +1=add1
(Π ((n Nat))
(= Nat (+ 1 n) (add1 n))))
(define +1=add1
(λ (n) ; λ 对应 Π
(same (add1 n)))) ; same 对应 =,(add1 n) 为 normal form
For every Nat n, (incr n) is equal to (add1 n).
Neutral Expressions
incr=add1 (claim)
(claim incr=add1
(Π ((n Nat))
(= Nat (incr n) (add1 n))))
由于 (incr n) 化简到 (iter Nat n 1 (+ 1)) 时已经是一个 neutral expression(无法继续 evaluate),所以不能和 +1=add1 一样用 (same (add1 n)) 来证明。
Neutral Expressions
(Neutral Expressions)
Variables that are not defined are neutral. If the target of an eliminator expression is neutral, then the eliminator expression is neutral.
并非所有含变量的表达式都是 neutral expression。例如 (λ (x) (add1 x)) 含有变量,但是它是 value(constructor 是 λ)。
Neutral ≠ Normal
一些 neutral expressions 是非 normal 的。
- Top constructor 为 Π 的 neutral expression
f是非 normal 的- 利用 eta-rules,
f等价于(λ (x) (f x)) - 后者是 normal 的,而前者不是(二者等价,而 normal form 只有一个)。
- 利用 eta-rules,
- Pair 类似
- 假设
p是(Pair A D),其等价于(Pair (car p) (cdr p)) - 后者才是 normal form,而所有的 neutral pair 都不是 normal 的。
- 假设
像这种尽量地利用了 eta-rule 来创建 value,使得 top constructor 和类型相对应(Π 对应 λ,Pair 对应 cons),而且它们都不能进行 beta 规约,这样的 normal form 被称为 η-long normal forms。
在 =-表达式中,neutral expressions 会作为参数经常出现。
incr=add1:definition
Expressions, however, can encode interesting patterns of reasoning, such as using induction to try each possibility for the variable in a neutral expression.
即便 incr 和 add1 不是 “same” 的,也可以使用归纳可以证明 incr=add1。
(define incr=add1
(λ (n)
(ind-Nat n
mot-incr=add1
base-incr=add1 ; 读作 the base for incr=add1
step-incr=add1)))
base
(claim base-incr=add1
(= Nat (incr zero) (add1 zero)))
(define base-incr=add1
(same (add1 zero)))
(incr zero) 不是 neutral 的,所以可以直接 same。
mot
motive 的类型由 incr=add1 可以显然得到。
(claim mot-incr=add1
(→ Nat
U))
(define mot-incr=add1
(λ (k)
(= Nat (incr k) (add1 k))))
step
step 的类型比较显然。
(claim step-incr=add1
(Π ((n-1 Nat))
(→ (mot-incr=add1 n-1)
(mot-incr=add1 (add1 n-1)))))
;; 展开
(claim step-incr=add1
(Π ((n-1 Nat))
(→ (= Nat
(incr n-1)
(add1 n-1))
(= Nat
(incr (add1 n-1))
(add1 (add1 n-1))))))
其中 → 表达式可以理解为 if...then...(归纳步骤)。
(“If” and “Then” as Types)
The expression
(→ X Y)can be read as the statement, “if X then Y.”注解:之所以可以这样,是因为这里都是 total functions。
又因为 Π 表达式可以理解为 every,=-表达式可以理解为 equals,所以原来的式子可以读作:
For every Nat
n,if
(incr n)equals(add1 n),then
(incr (add1 n))equals(add1 (add1 n))
(incr (add1 n-1)) = (add1 (incr n-1))
为了证明这个,我们还需要另一个 incr 其他的性质。
(incr (add1 n-1))=
(iter-Nat (add1 n-1) 1 (+ 1))=
(add1 (iter-Nat n-1 1 (+ 1)))
即,我们发现 (incr (add1 n-1)) ~ (add1 (incr n-1))。所以 claim 可以写成下面的形式:
(claim step-incr=add1
(Π ((n-1 Nat))
(→ (= Nat
(incr n-1)
(add1 n-1))
(= Nat
(add1 ; 这个表达式变了
(incr n-1))
(add1
(add1 n-1))))))
所以我们的目标是从 (= Nat (incr n-1) (add1 n-1)) 到 (= Nat (add1 (incr n-1)) (add1 (add1 n-1)))。
cong
cong 是 = 的 eliminator,类似于 map,可以将证明 a = b 变成证明 f(a) = f(b)。
(The Law of
cong)If
fis an(→ X Y)andtargetis an(X from to)=, then(cong target f)is an(= Y (f from) (f to)).
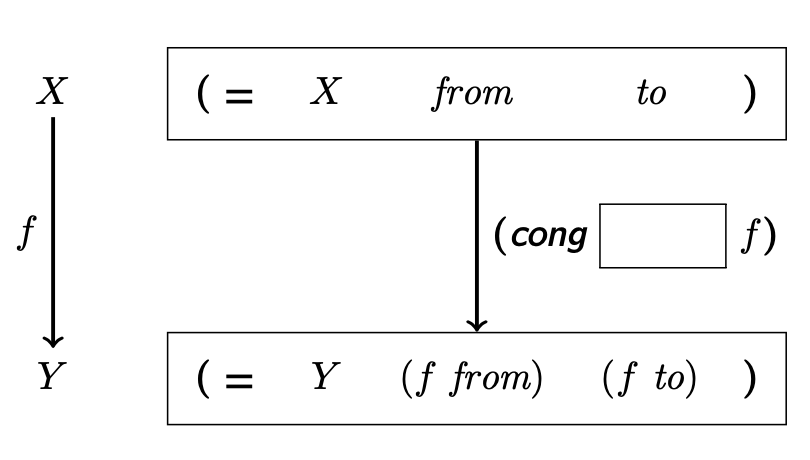
Figure 1: cong
可以发现 cong 的作用是同时对等式两边进行变换,直到使二者变为一个已知的 statement。
我们希望把 (incr n-1) 变成 (add1 (incr)),所以 f 可以用 (+ 1)。这里不能用 add1 和 incr:前者是一个 constrcutor 而非 expression,不能接受参数;后者不能得到一个 incr。而 (+ 1) 既可以接受参数又可以生成一个 add。
(define step-incr=add1
(λ (n-1)
(λ (incr=add1_n-1)
(cong incr=add1_n-1 (+ 1)))))
使用 ind-Nat 与 cong 归纳
对于 incr=add1 要使用 ind-Nat,而对于 +1=add1 不用,因为前者是一个 neutral expression 且 normal form 形式不一样,而后者的 normal form 是相同的。Neutral expressions 是不可以被 evaluate 的,但是如果给其中的自由变量赋值,那么就能对其进行 evaluate。
和其它 eliminators 一样,cong 表达式第一步会先尝试 evaluate 它的 target(第一个参数,即一个 =-表达式):
- 如果 target 不是 neutral 的,那么整个表达式
(cong (same x) f)会被化简成(same (f x)) - 如果 target 是 neutral 的,那么整个
cong表达式也是 neutral 的
(The Commandment of
cong)If
xis anX, andfis an(→ X Y), then(cong (same x) f)is the same(= Y (f x) (f x))as(same (f x))