本章将考虑把 System F 与 subtyping 结合的类型系统。
Motivation
考虑一个 subtyping 系统中的例子:
f = λx : {a: Nat}. {orig=x, asucc=succ(x.a)};
(* f : {a:Nat} → {orig:{a:Nat}, asucc:Nat} *)
ra = {a=0};
(* ra : {a:Nat} *)
rab = {a=0, b=0};
(* rab : {a:Nat, b:Nat} *)
当这里应用 f ra 时,一切正常;但是应用 f rab 时,会因为类型签名的原因,orig 只保留了 a field,丢掉了 b field。在这里自然会想到利用 polymorphism 实现多态:
fpoly = λX. λx:X. {orig=x, asucc=succ(x.a)};
(* Error: x.a is invalid, expected record type *)
但是这里的 X 是一个类型变量,因此无法使用 x.a。为此需要能够为 polymophic function 加入类型变量的 subtyping constraint,从而让这个函数通过类型检查:
fpoly' = λX <: {a:Nat}. λx:X. {orig=x, asucc=succ(x.a)};
(* fpoly' : ∀X<:{a:Nat}. X → {orig:X, asucc:Nat} *)
这样的特性称为 bounded quantification,包含它的类型系统是 \( F_{<:} \)。
Definitions
形式上,\( F_{<:} \) 将 System F 与 subtyping 结合,并允许在量词中携带 subtyping constraints。实际上,有两种方式来定义 \( F_{<:} \) 的 subtyping,它们在 S-All 的形式化上有区别:容易处理但灵活性较差的版本称为 kernel 规则,另一种表达能力更强但在技术细节上略有问题的 full 规则。为了区分二者,分别将包含二者的系统称之为 kernel \( F_{<:} \) 与 full \( F_{<:} \)。
下面先介绍 kernel \( F_{<:} \) 的定义:

Figure 1: Bounded quantification (kernel ( F_{<:} ))
Bounded and Unbounded Quantification
从形式化中可以看出,\( F_{<:} \) 只提供了 bounded quantification,而不提供 unbounded quantification。这是因为前者已经包含了后者:
\[\forall X. T \overset{\text{def}}{=} \forall X <: \operatorname{\mathtt{Top}}. T\]
Scoping
在讨论 \( F_{<:} \) 前,需要先讨论一个技术细节:什么样的作用域与绑定是有效的?下面是几个例子:
- \( \Gamma = X <: \operatorname{\mathtt{Top}}, y : X \to \operatorname{\mathtt{Nat}} \) 这个绑定显然是有效的
- \( \Gamma = y : X \to \operatorname{\mathtt{Nat}}, X <: \operatorname{\mathtt{Top}} \) 这个绑定无效,因为无法明确 \( y \) 的绑定中的 \( X \) 是什么
- \( \Gamma = X <: \{ a : \operatorname{\mathtt{Nat}}, b : X \} \) 这个绑定看起来无效,但是它在 OOP 中非常常见,并且在 Generic Java 中使用,称为 F-bounded quantification。它的理论比 \( F_{<:} \) 稍微复杂一些,并且只在包括 recursive types 的系统中会变得有趣
- \( \Gamma = X <: \{ a : \operatorname{\mathtt{Nat}}, b : Y \}, Y <: \{ c : \operatorname{\mathtt{Bool}}, d : X \} \) 这个绑定引入了相互递归的类型变量 \( X \) 和 \( Y \),它们的定义相互依赖。这种形式描述相互引用的 subtyping 约束
在本章中为了方便期间,只考虑第一种情况。
Subtyping
类型变量在 \( F_{<:} \) 中拥有相关联的 bounds,如 S-TVar 所描述的。在 \( F_{<:} \) 中,\( <: \) 变成了一个三元关系 \( \Gamma \vdash X <: T \),其含义为“类型变量 \(X\) 在假设 \(\Gamma\) 下是类型 \(T\) 的子类型”。类似的,需要为 T-TAbs 和 T-TApp 添加 bounds。
由于给每个类型变量都加上了 bounds,因此需要考虑在全称量词下的子类型关系。在上图关于 kernel-\(F_{<:}\) 的形式化中给出的 S-All 是一个简化版本,称为 kernel 规则,它要求子类型关系中的全称量词的 upper bounds 必须是相同的。
Full \( F_{<:} \)
然而正如上面所说的,还有一种 full 规则,没有 kernel 规则的限制,即它允许全称量词的 upper bounds 是不同变量。
这里可以把全称量词看作是一个“types to terms”的函数,那么带有全称量词的类型的 subtyping 关系就可以看成是一个协变关系。在 kernel 规则中,要求参数是不变的,而返回值是协变的,这一点显然引入了额外的限制。如果要放宽这个限制,那么根据类比很容易想到函数参数部分应该是反变的,下面来讨论这种情况。
将全称量词看作是“函数”后,那么类型 \( T = \forall X \mathrel{{\raisebox{0.1ex}{\scriptsize$<$}}\!\colon} T_1. T_2\) 可以看作是一个“将 \( T_1 \) 的 subtypes 映射到类型为 \( T_2 \) 的 terms 上”的函数。令 \( S = \forall X <: S_1. S_2\),其中 \( T_1 <: S_1 \),也就是说 \(\operatorname{\mathrm{dom}}(T) \subseteq \operatorname{\mathrm{dom}}(S)\)。所以用到 \(T\) 的地方可以用 \(S\) 替换,根据 principle of safe substitution 有 \( S <: T \)。此时类似箭头类型,要求 \( \Gamma, X <: T_1 <: S_1 \vdash S_2 <: T_2 \),即 \( \Gamma, X <: T_1 \vdash S_2 <: T_2 \)。
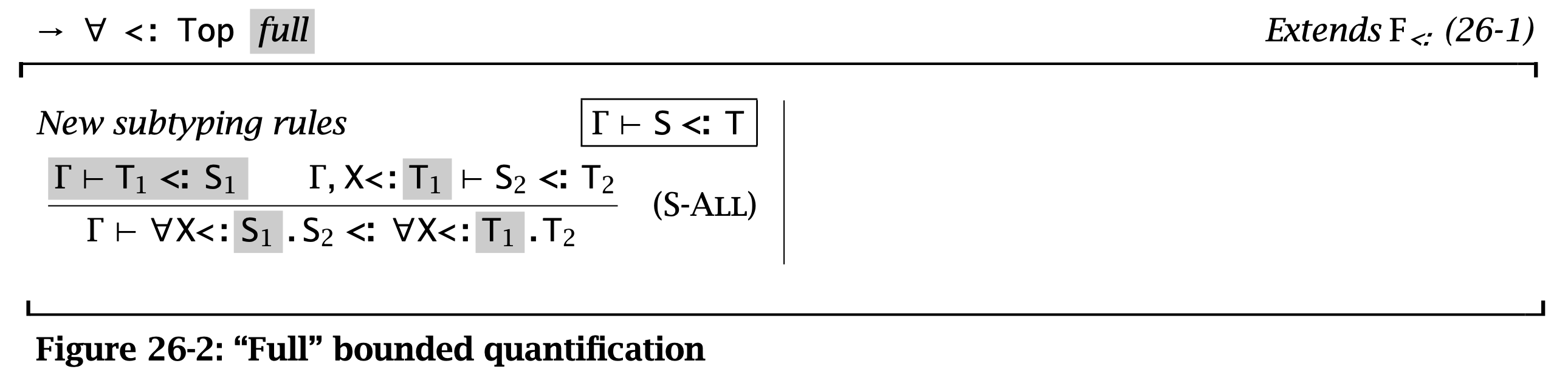
Figure 2: Bounded quantification (full ( F_{<:} ))