Motivation
Existential types 记作 \( \{ \exists x, T\} \) 并不比 universal types 复杂,但是它的 motivation 和 elimination forms 会稍微复杂一些。
上一章引入的 universal types 可以用两种视角看待:
- logical intuition:类型为 \( \forall X. T \) 由 value 构成,对于任意的类型 \( S \),其中的 value 拥有类型 \( [X \mapsto S]T \)。这种 intuition 对应了类型擦除。即将 \( \forall X. T \) 与 \( T \) 对应。
- operational intuition:\( \forall X. T \) 由函数构成,其中的函数将类型 \( S \) 映射到类型为 \( [X \mapsto S]T \) 的 term。这种 intuition 对应了 System F 的形式化定义(\( \lambda X. \lambda x. t \)),将 type application 看作计算的一步。
类似的,existential types 也有两种视角:
- logical intuition:类型为 \( \{ \exists X, T \} \) 由 value 构成,对于某些类型 \( S \),其中的 value 拥有类型 \( [X \mapsto S]T \)。
- operational intuition:\( \{ \exists X, T \} \) 由 pair 构成,记作 \( \{*S, t\} \),第一项为类型 \( S \),第二项是类型为 \( [X \mapsto S]T \) 的 term \( t \)。
本章将更强调 operational intuition,因为它和编程语言中的 modules 以及 abstract data types 有密切联系。因此这里将其记作 \( \{\exists X, T\} \) 而不是 \( \exists X. T \) 以此来强调它和 pairs 的关系。
要引入 existential types,关键是理解如果 introduce 其中的元素(即 pairs),以及如何在计算中 eliminate。
Analogy with Packages or Modules
一个 existential type 的 value 形如 \( \{*S, t\} \),此处 \( * \) 用作和 tuples 间的区分。另一种记法是 \( \operatorname{\mathtt{pack}}\ X = S\ \operatorname{\mathtt{with}}\ t \)。一个有用的直觉是将其看作带有一个隐藏的 type component 和一个隐藏的 term component 的 package 或者 module。其中,类型 \( S \) 称为 hidden representation type 或 witness type。从这可以看出,existential types 和 OCaml 中的 abstract module 有着密切关联。
例如 package \( p = \{ *\operatorname{\mathtt{Nat}}, \{a = 5, f = \lambda x: \operatorname{\mathtt{Nat}}. \operatorname{\mathtt{succ}}(x)\} \} \) 的类型为 \( \{ \exists X, \{a: X, f : X \to X\}\} \)。其中 type component 是 \( \operatorname{\mathtt{Nat}} \),value component 是一个 record,包括 \( a \) 和 \( f \)。同时,这个 package \( p \) 也具有类型 \( \{ \exists X, \{a : X, f : X \to \operatorname{\mathtt{Nat}}\}\} \)。
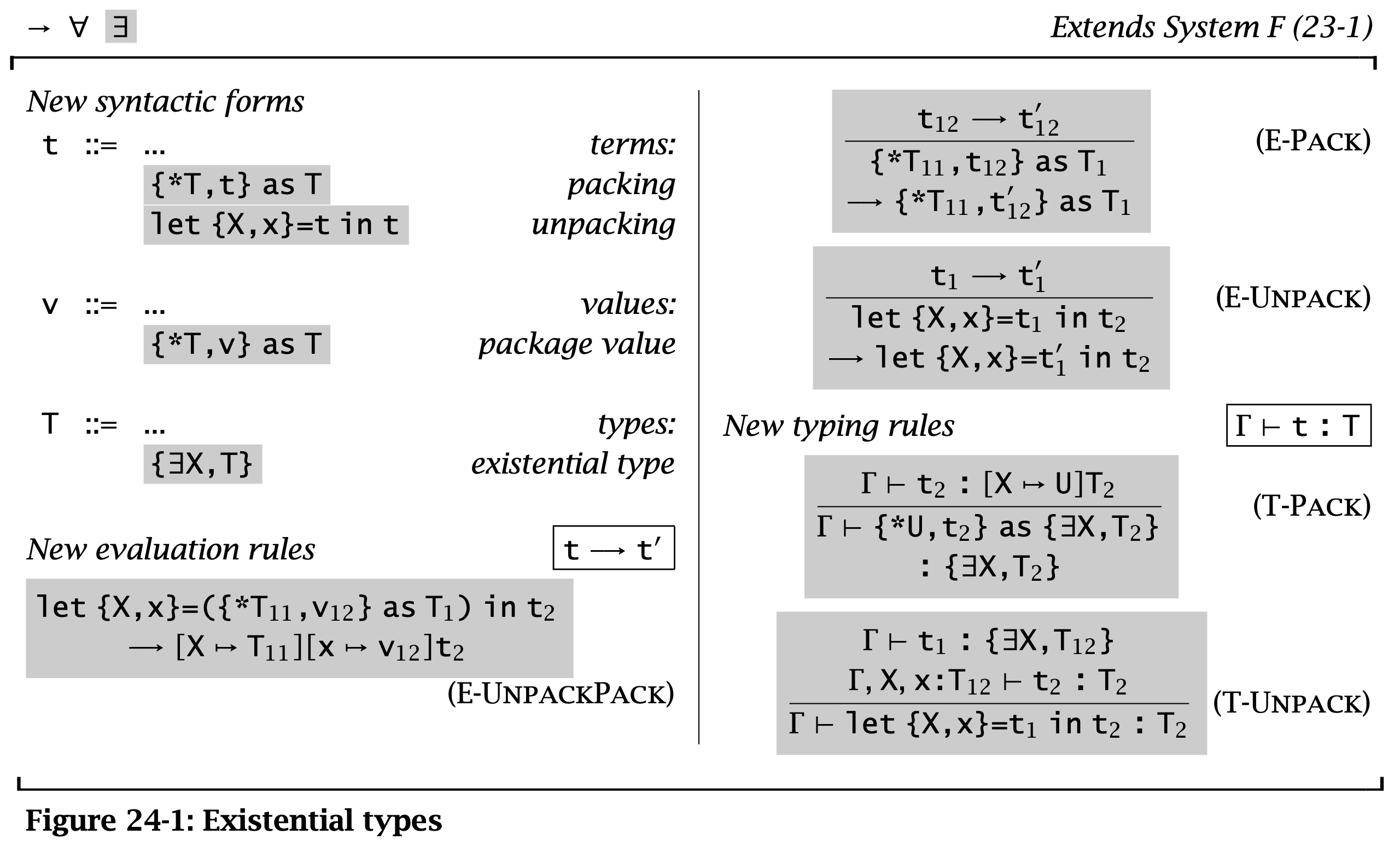
Figure 1: Existential types
这表明 typechecker 无法决定 package 的具体类型,需要程序员根据意图决定具体类型(见 T-Pack)。代码如下:
p = {*Nat, {a = 5, f = λx: Nat. succ(x)}} as {∃ X, {a: X, f: X → X}};
(** p : {∃ X, {a: X, f: X → X}} *)
p1 = {*Nat, {a = 5, f = λx: Nat. succ(x)}} as {∃ X, {a: X, f: X → Nat}};
(** p1 : {∃ X, {a: X, f: X → Nat}} *)
同样,一个 existential type 也可以有多种 hidden representation types:
p2 = {*Nat, 0} as {∃ X, X};
(** p2 : {∃ X, X} *)
p3 = {*Bool, true} as {∃ X, X};
(** p3 : {∃ X, X} *)
将 existential types 看作 package 或 module 也可以更好理解其 elimination 的操作。在 package / module 中会使用 open 或者 import 来引用其中的元素。类似的,可以使用 pattern-matching 实现类似的效果(见 T-Unpack)。即将 \( t₁ \) 中的 type component 和 term component 提取出来。另一种写法是 \( \operatorname{\mathtt{open}}\ t₁\ \operatorname{\mathtt{as}}\ \{X, x\}\ \operatorname{\mathtt{in}}\ t₂ \)。
下面是一个例子,其中提取出来的 type 和 term 都可以使用:
p4 = {*Nat, {a = 0, f = λx: Nat. succ(x)}} as {∃ X, {a: X, f: X → Nat}};
(** p4 : {∃ X, {a:X, f:X→Nat}} *)
let {X, x} = p4 in (x.f x.a);
(** 1 : Nat *)
let {X, x} = p4 in (λy: X. x.f y) x.a;
(** 1 : Nat *)
需要注意的是 existential type 中的 representation type 在类型检查的过程中是不可见(abstract)的,因此 elimination 提取出来的具体类型也是不可见的。这是因为 existential type 可以有多种不同的 hidden representation types。因此在类型检查的过程中只能使用抽象的类型。
let {X, x} = p4 in succ (x.a);
(** Error: argument of succ is not a number *)
另一个不易发现的错误是 elimination 后整个语句的返回类型。例如下面语句的具体返回类型是 \( \operatorname{\mathtt{Nat}} \),在类型检查时是 \( X \),而 \( X \) 只在 let-clause 中可见,因此会出错:
let {X, x} = p4 in x.a;
(** Error: Scoping error! *)
Elimination 对应的计算规则是 E-UnpackPack,在 module 中这条规则可以看成链接(linkage),即将引用外部模块的符号替换为其具体内容。在这条规则下,上面 ill-typed 的例子随着计算的进行也会变成 well-typed term。
Data Abstraction with Existentials
Existential types 在大规模程序中提供了一种数据抽象的方式,将程序分为不同的模块。本章将用 existential types 作为框架考虑传统的 abstract data types 和 objects。
本节中的实例都采用纯函数式,因为模块化和抽象机制与是否有副作用无关,因此讨论能更加简洁。
Abstract Data Types
为了方便起见,下面的 ADT 都代指 abstract data types。
ADT 包括以下几个部分:
- abstract type \( A \)
- abstract type 对应的 concrete representation type \( T \)
- 创建、查询或操作 \( T \) 类型 value 的过程的实现
- representation 和过程间的 abstraction boundary
在 abstraction boundary 内,元素被视作类型 \( T \),在 boundary 外,元素被视作类型 \( A \)。当 value 作为 \( A \) 时能被传递和存储,但是不能直接查看和操作内部,而是只能使用 ADT 提供的操作。下面是一个例子:
ADT counter =
type Counter
representation Nat (** type Counter = Nat *)
signature
new : Counter,
get : Counter → Nat,
inc : Counter → Counter;
operations
new = 1,
get = λi: Nat. i,
inc = λi: Nat. succ(i);
(** Usage *)
counter.get (counter.inc counter.new);
在这个例子中,ADT counter 的名字是 Counter,representation type 是 Nat,signatures 和 operations 中分别定义了这三个 operations 的签名和具体实现,ADT 的整体定义是抽象边界。这个 ADT 定义可以翻译成:
counterADT =
{ *Nat,
{ new = 1,
get = λi: Nat. i,
inc = λi: Nat. succ(i) } }
as { ∃ Counter,
{ new: Counter,
get: Counter → Nat,
inc: Counter → Counter } };
(** counterADT :
{ ∃ Counter,
{ new : Counter,
get : Counter → Nat,
inc : Counter → Counter } } *)
let {Counter, counter} = counterADT in
counter.get (counter.inc counter.new);
(** 2 : Nat *)
注意在这个例子中,Counter 被实例化成了 Nat,因此 get 和 inc 的参数实际也是 Nat 类型的。这里的 abstract type 有点类似 Self。
一个大型程序可以被分解为多个 ADT,并且一个 ADT 定义完成后可以用于另一个 ADT 的定义,这样就将大型程序打包成了一个干净的抽象。这里通过 ADT 隐藏信息实现了 representation independence,这样可以在不改变 ADT 提供的接口的前提下,改变其内部的实现,而不影响使用它的程序,例如:
counterADT =
{ *{x : Nat},
{ new = { x = 1 },
get = λi: { x : Nat }. i.x,
inc = λi: { x : Nat }. { x = succ(i.x) } } }
as { ∃ Counter,
{ new : Counter,
get : Counter → Nat,
inc : Counter → Counter } };
(** counterADT :
{ ∃ Counter,
{ new : Counter,
get : Counter → Nat,
inc : Counter → Counter } } *)
基于 ADT 的编程风格可以极大提高大型系统的可维护性。这样做有几个原因。首先,这种风格限制了对程序的更改范围;其次,它鼓励程序员限制程序各部分之间的依赖关系,并缩短 ADT 的签名;最后,它通过明确的签名迫使程序员考虑设计抽象。
此处定义的 ADT 其实形式上便类似于 typeclass 或者 trait。在 Scala 中定义 typeclass pattern F,然后对 A 进行 instantiation 时会得到一个 F<A>,这里的 A 便是 inner representation type。ADT 中的 abstract type 对应了 trait 中的 Self。二者的区别在于每次使用 existential types 时需要显式地进行 instantiation,传入类型以及内部字段;而使用 typeclass 或者 trait 这个过程是自动完成的。
这里在定义 ADT 时,会先定义其类型 counterADT,然后立即用 let 打开它并进行操作,这是使用 ADT 编程的特征。下面一节将基于 existential objects 来进行抽象。
Existential Objects
本章仍然使用函数式计数器作为例子:
Counter = { ∃ X,
{ state : X,
methods : { get : X → Nat, inc : X → X } } };
c = { *Nat,
{ state = 5,
methods =
{ get = λx: Nat. x,
inc = λx: Nat. succ(x) } } }
as Counter;
(** c : Counter *)
let { X, body } = c in body.methods.get(body.state);
(** 5 : Nat *)
然而在这里直接调用 inc 会报错,因为根据签名它返回的是 Counter 而不是 Nat:
let {X, body} = c in body.methods.inc(body.state);
(** Error: Scoping error! *)
解决方案是在 let 内直接创建新的 Counter:
c1 = let {X, body} = c in
{ *X,
{ state = body.methods.inc(body.state),
methods = body.methods } }
as Counter;
(** c1 : Counter *)
这里还缺失了很多特性,例如 self 等,需要 higher-order systems 完成。
Objects vs. ADTs
比较 objects 和 ADTs 可以发现很多不同点。
第一点是使用方式上的区别。ADT 会在构建 package 后立刻打开,内部是打包的类型和操作;objects 会尽量保持封闭,封装了内部状态和方法。这点导致了很多使用场景的区别:
- ADT 中的
Counter是内部的 abstract type,在运行时是统一的 concrete type;objects 中的c是一个完整的 existential object,携带了内部状态和操作; - 在运行时,ADT 在运行时是相同的 internal representation type,需要有一个的
counter携带操作;而每个 objects 都可以有自己的 internal representation type 和 methods。
这些区别让二者的使用场景不同。Objects 在 subtyping 和 inheritance 中使用非常方便,可以先一个父类,然后为每个 objects 进行细化。虽然每个细化都有不同的内部实现,但是它们呈现出来的类型都是统一的 existential type,因此可以被通用代码使用,并被一起存储。而 ADT 则不能这样做,除非其内部使用 variants 为每种不同的 objects 做区分。
第二点是对于接受同样类型的二元操作的区别。
- 一些二元操作可以完全通过公开操作实现。例如要实现
Counter的相等操作,只需要先用get询问当前值然后比较,这样相等操作可以在抽象边界之外完成,这类操作称为 weak binary operations; - 无法完全通过公开操作实现,必须访问内部封装实现的二元操作称为 strong binary operations。
Weak binary operations 比较简单,因为将其放在抽象边界内部和外部都没有区别,不过放在内部可能会需要递归类型参与。
Strong binary operations 则必须在内部实现。此时的问题是,尽管我们可以获得当前所属 object 中的状态,但是无法获得另一个 object(rhs)内部的状态,因为虽然它们类型相同,但是具体定义未必相同。因此 objects 则必须放弃使用 strong binary operations。
当然这里提到的限制都是在纯函数式的模型下。C++ 或者 Java 等主流面向对象语言在设计时便允许类定义 strong binary operations。在这些语言中,对象的类型就是类名。相同类名的对象提供的内部状态和操作完全相同,并且子类只能在继承的基础上添加新的实例变量,这确保访问另一个对象完全没有阻碍。
Encoding Existentials
下面利用 universal types 定义 existential types。在 universal types 下,pair 可以表示成:
\[ \operatorname{\mathtt{Pair}}\ X\ Y = \forall R. (X \to Y \to R) \to R; \]
因此有:
\[ \{ \exists X, T \} \overset{\text{def}}{=} \forall Y. (\forall X. T \to Y) \to Y \]
换句话说,existential package 被视为一个 value,给定一个 result type 和一个 continuation,将自身传入 continuation 以产生 result。Continuation 接受一个类型 \( X \) 和一个 term \( T \)。
\( \{ *S, t \}\ \operatorname{\mathtt{as}}\ \{ \exists X, T \} \) 的编码可以根据类型推导得到:
\[ \{ *S, t \}\ \operatorname{\mathtt{as}}\ \{ \exists X, T \} \overset{\text{def}}{=} \lambda Y. \lambda f: (\forall X. T \to Y). f\ [S]\ t \]
接下来考虑 \( \operatorname{\mathtt{let}}\ \{X, x\} = t_1\ \operatorname{\mathtt{in}}\ t_2 \)。首先根据类型规则有 \( t₁ : \{ \exists X, T_{11} \} = \forall Y. (\forall X. T_{11} \to Y) \to Y \),且 \( t₂ : T₂ \),根据类型容易得到结果:
\[ \operatorname{\mathtt{let}}\ \{X, x\} = t_1\ \operatorname{\mathtt{in}}\ t_2 \overset{\text{def}}{=} t_1\ [T₂]\ (\lambda X. \lambda x: T_{11}. t_2) \]
相当于将 \( (\lambda X. \lambda x: T_{11}. t_2) \) 作为 continuation 传入 \( t_1 \) 计算。
另一个有趣的 encoding 是从 C-H 同构得到的:
\[ (\exists x. P(x)) \to Q \iff \forall x. P(x) \to Q \]
如果把 universal types 对应 type erasure,那么 existential types 对应 monomorphization,而这个恒等式说明二者可以互相转换。
类似 universal types,函数返回值处的 \( \exists \) 也可以也可以移动到头部:
\[ P \to \exists x. Q(x) \iff \exists x. P \to Q(x) \]