前面介绍的类型系统中的每个地方(特别是 lambda abstraction 中)都要求明确标注类型参数。本章探讨一种 type reconstruction 的技术,使得在部分或全部类型未标注的情况下计算出一个 principal type。Type reconstruction 涉及到 record types 和 subtyping 的时候会变得有些微妙,因此为了简化问题,这里只考虑 STLC。
本章介绍的 type reconstruction 允许用户部分标注类型,然后由 type checker 一边检查类型,一边推断未标注的类型。另一个场景是用户没有标注任何类型,完全由编译器推导,其对应的算法称为 Algorithm W,可以看作本章的一个特例。
Type Variables and Substitution
(type substitution)
Formally, a type substitution is a finite mapping from type variables to types. We write \( [X \mapsto T] \) for the substitution that associates \( X \) with \( T \).
We write \( \operatorname{\mathtt{dom}}(\sigma) \) for the set of type variables appearing on the left-hand sides of pairs in \( \sigma \), and \( \operatorname{\mathtt{range}}(\sigma) \) for the set of types appearing on the right-hand sides.
Note that the same variable may occur in both the domain and the range of a substitution. Like term substitutions, all the clauses of the substitution are applied simultaneously; for example, \( [X \mapsto \operatorname{\mathtt{Bool}}, Y \mapsto X \to X] \) maps \( X \) to \( \operatorname{\mathtt{Bool}} \) and \( Y \) to \( X \to X \), not to \( \operatorname{\mathtt{Bool}} \to \operatorname{\mathtt{Bool}} \).
\[\sigma(X) = \begin{cases} T, & \text{if } (X \mapsto T) \in \sigma \\ X, & \text{if } X \notin \operatorname{\mathtt{dom}}(\sigma) \end{cases}\]
\[\sigma(T₁ \to T₂) = \sigma(T₁) \to \sigma(T₂)\]
Note that we do not need to make any special provisions to avoid variable capture during type substitution, because there are no constructs in the language of type expressions that bind type variables.
Type substitution is extended pointwise to contexts by defining:
\[\sigma(x₁:T₁,…,xₙ:Tₙ) = (x₁:\sigma(T₁),…,xₙ:\sigma(Tₙ))\]
Similarly, a substitution is applied to a term \( t \) by applying it to all types appearing in annotations in \( t \).
If \( \sigma \) and \( \gamma \) are substitutions, we write \( \sigma \circ \gamma \) for the substitution formed by composing them as follows:
\[(\sigma \circ \gamma) = \begin{cases} X \mapsto \sigma(T), & \text{if $X \mapsto T \in \gamma$} \\ X \mapsto T, & \text{if $X \mapsto T \in \sigma \land X \notin \operatorname{\mathtt{dom}}(\gamma)$} \end{cases}\]
Note that \( (\sigma \circ \gamma) S = \sigma(\gamma S) \).
(Preservation of typing under type substitution)
If \( \sigma \) is any type substitution and \( \Gamma \vdash t : T \), then \( \sigma \Gamma \vdash \sigma t: \sigma T \).
对 type derivation 进行归纳即可。
Two Views of Type Variables
对于一个包含类型变量的类型,我们可以有两种不同的视角:
- forall:类型检查时应该将类型变量保持抽象,将它替换成任意类型都保证这个表达式是 well-typed 的。这引入了 parametric polymorphism 的概念。
- exists:存在类型变量的表达式可以不是 well-typed 的,但是类型重建算法应当找到一个实例化的类型使它 well-typed。
类型重建的目标就是后者,即找到能够使得整个程序通过类型检查的最一般的类型。
一些语言会在 parsing 阶段给 lambda abstraction 的参数添加类型(例如将 \( \lambda x. t \) 变成 \( \lambda x: X. t \))然后进行类型重构,找到类型变量的最一般值。
(Solution)
Let \(\Gamma\) be a context and \(t\) a term. A solution for \((\Gamma,t)\) is a pair \((\sigma,T)\) such that \( \sigma \Gamma \vdash \sigma t : T \).
Constraint-Base Typing
为了解决这个问题,接下来介绍一个算法。对于给定的 \(t\) 和 \(\Gamma\) 的情况下,它能计算出一组 \((\Gamma, t)\) 必须满足的类型约束(类型方程)。其原理与类型检查算法类似,但是它不“检查”约束是否成立,而是将这些约束“记录”下来。例如对于表达式 \(t_1\ t_2\),已知 \(\Gamma \vdash t_1 : T_1\) 和 \(\Gamma \vdash t_2 : T_2\) 时,算法并不会检查 \(t_1\) 是否具有 \(T_2 \to T_{12}\) 的形式,而是创建一个新的类型变量 \(X\),记录约束 \(T_1 = T_2 \to X\),并将 \(X\) 作为返回类型。
(Constraint Set)
A constraint set \( C \) is a set of equations \( \{S_i = T_i^{i \in 1 \dots n}\} \).
A substitution \( \sigma \) is said to unify an equation \( S = T \) if the substitution instances \( \sigma S \) and \( \sigma T \) are identical.
We say that σ unifies (or satisfies) \( C \) if it unifies every equation in \( C \).

Figure 1: Constraint Typing Rules
(Constraint Typing Relation)
The constraint typing relation \( \Gamma \vdash t : T \vert_\chi C \) is defined by the rules in Figure 22-1.
Informally, \( \Gamma \vdash t : T \vert_\chi C \) can be read: term \( t \) has type \( T \) under assumptions \( \Gamma \) whenever constraints \( C \) are satisfied.
In rule T-App, we write \( FV(T) \) for the set of all type variables mentioned in \( T \).
这里引入 \( \chi \) 记录新引入的变量的集合。这样能保证选取的新类型变量是一个 fresh variable,且已有的类型变量不会冲突。为了简化符号,后面讨论时可以省略这一点。
Constraint typing relation 和之前的 typing rules 的区别在于前者的 derivations 不会 fail,并且结果(\( C \) 和 \( T \))由 \( \Gamma \) 和 \( t \) 唯一决定;而后者有可能会 fail。Constraint typing relation 将 type reconstruction 的过程分成了两步,首先对于给定的 \( t \) 和 \( \Gamma \) 收集约束 \( C \) 并使用约束中出现的结果类型变量 \( S \) 来表示 \( t \) 的可能类型,然后为了确定 \( t \) 的类型解找能够满足约束 \( C \) 的替换 \( \sigma \)。如果没有替换 \( \sigma \) 满足条件,那么说明 \( t \) 无法通过类型检查。
下面是一个例子:假设 term \( t = \lambda x: X \to Y. x\ 0 \),可以得到一个 constraint set \( C = \{X \to Y = \operatorname{\mathtt{Nat}} \to Z\} \}, \chi = \{ Z \}, t: (X \to Y) \to Z\),对应的替换可以是 \( \sigma = [X \mapsto \operatorname{\mathtt{Nat}}, Y \mapsto \operatorname{\mathtt{Bool}}, Z \mapsto \operatorname{\mathtt{Bool}}] \)。
(Solution for Constraint Typing)
Suppose that \( \Gamma \vdash t : S | C \). A solution for \( (\Gamma,t,S,C) \) is a pair \( (\sigma, T) \) such that \( \sigma \) satisfies \( C \) and \( \sigma S = T \).
到目前以为出现了两个 solutions 的定义,一个是 declarative 的原始定义,另一个是 constraint-based 的定义。下面的定理表明这两个定义是等价的。
(Soundness of constraint typing)
Suppose that \( \Gamma \vdash t : S | C \). If \( (\sigma, T) \) is a solution for \( (\Gamma, t, S, C) \), then it is also a solution for \( (\Gamma, t) \).
这个证明中 \( \chi \) 是次要的,可以省略。对 constraint typing 的推导进行归纳,设 \( (\sigma, T) \) 是 \( (\Gamma, t, S, C) \) 的解:
CT-Var:\( t = x \qquad x : S \in \Gamma \qquad C = \{\} \)由于 \( C \) 是空集,因此只需满足 \( \sigma S = T \)。由于 \( x : S \in \Gamma \),即 \( \Gamma \vdash x : S \),因此 \( \sigma \Gamma \vdash x : T \)。
CT-Abs:\( t = \lambda x:T₁.t₁ \qquad S = T₁ \to S₂ \qquad \Gamma, x:T₁ \vdash t₁ : S₂ \vert C₁ \)\( \sigma \) unifies \( C \) 且根据定义有 \( T = \sigma S = \sigma T₁ \to \sigma S₂ \),因此 \( (\sigma, \sigma S₂) \) 是 \( ((\Gamma, x: T₁), t₂, S₂, C) \) 的解。根据归纳假设,\( (\sigma, \sigma S₂) \) 是 \( ((\Gamma, x:T₁), t₂) \) 的解,。因此有 \( \sigma \Gamma, x:\sigma T₁ \vdash \sigma t₂ : \sigma S₂ \),根据
T-Abs可得 \( \sigma \Gamma \vdash \lambda x:\sigma T₁.\sigma t₂ : \sigma T₁ \to \sigma S₂ = T \)。CT-App:\( t = t₁\ t₂ \qquad S = X \qquad \Gamma \vdash t₁ : S₁ | C₁ \qquad \Gamma \vdash t₂ : S₂ | C₂ \qquad C = C₁ \cup C₂ \cup \{S₁ = S₂ \to X\} \)\( \sigma \) unifies \( C₁, C₂ \) 且 \( \sigma S₁ = \sigma S₂ \to \sigma X \)。因此 \( (\sigma, \sigma S₁) \) 和 \( (\sigma, \sigma S₂) \) 分别是 \( (\Gamma, t₁, S₁, C₁) \) 和 \( (\Gamma, t₂, S₂, C₂) \) 的解。根据归纳假设,因此有 \( \sigma \Gamma \vdash \sigma t₁ : \sigma S₁ \) 和 \( \sigma \Gamma \vdash \sigma t₂ : \sigma S₂ \)。
又由于 \( \sigma S₁ = \sigma S₂ \to \sigma X \),因此有 \( \sigma \Gamma \vdash \sigma t₁ : \sigma S₂ \to \sigma X \)。根据
T-App可得 \( \sigma \Gamma \vdash \sigma t₁\ \sigma t₂ : \sigma X = T \)。其他情况类似。
Completeness 的证明比较复杂,特别需要注意引入的新变量。
Write \( \sigma ∖ \chi \) for the substitution that is undefined for all the variables in \( \chi \) and otherwise behaves like \( \sigma \).
这个定义可以理解为 \( \sigma ∖ \chi \) 是在 \( \sigma \) 中去掉 \( \chi \) 中变量的替换的结果。下面在 completeness 中要求两个解满足 \( \sigma’ \setminus \chi = \sigma \),这使得两种解的区别仅仅在于新引入的变量,而不影响其他结果。
(Completeness of constraint typing)
Suppose \( \Gamma \vdash t : S \mid_\chi C \). If \( (\sigma, T) \) is a solution for \( (\Gamma, t) \) and \( \operatorname{\mathrm{dom}}(\sigma) \cap \chi = \emptyset \), then there is some solution \( (\sigma’, T) \) for \( (\Gamma, t, S, C) \) such that \( \sigma’ ∖ \chi = \sigma \).
对 constraint typing 的推导进行归纳,设 \( (\sigma, T) \) 是 \( \Gamma, t \) 的解:
CT-Var:\( t = x \qquad x : S \in \Gamma \)根据假设有 \( \sigma \Gamma \vdash x : T \)。根据 STLC 的 inversion lemma,有 \( x : T \in \sigma \Gamma \),因此 \( \sigma S = T \)。因此 \( \sigma \) 是 \( (\Gamma, t, S, \{\}) \) 的解。
CT-Abs:\( t = \lambda x:T₁.t₂ \qquad \Gamma, x:T₁ \vdash t₂ : S₂ \mid_\chi \qquad S = T₁ \to S₂ \)根据 STLC 的 inversion lemma,存在 \( T₂ \) 使得 \( \sigma \Gamma, x : \sigma T₁ \vdash \sigma t₂ : T₂ \) 且 \( T = \sigma T₁ \to T₂ \)。
根据归纳假设,存在 \( (\sigma’, T₂) \) 是 \( ((\Gamma, x:T₁), t₂, S₂, C) \) 的解且 \( \sigma’ ∖ \chi = \sigma \)。由于 \( x : T₁ \) 不会引入任何类型变量(\( T₁ \) 是在 parsing 阶段补充的),所以此处的 \( \chi \) 中不会包含 \( T₁ \) 中出现的类型变量,因此 \( \sigma’ T₁ = \sigma T₁ \)。
由于 \( \sigma’(S) = \sigma’(T₁ \to S₂) = \sigma’ T₁ \to \sigma’ S₂ = \sigma T₁ \to \sigma’ S₂ = \sigma T₁ \to T₂ = T \),因此 \( (\sigma’, T) \) 是 \( (\Gamma, (\lambda x : T. t₂), T₁ \to S₂, C) \) 的解。
CT-App\[ t = t₁\ t₂ \qquad \Gamma \vdash t₁ : S₁ \mid_{\chi₁} C₁ \qquad \Gamma \vdash t₂ : S₂ \mid_{\chi₂} C₂ \qquad S = X \] \[\chi₁ \cap \chi₂ = \chi₁ \cap FV(T₂) = \chi₂ \cap FV(T₁) = \emptyset \qquad \text{$X$ not mentioned in $\chi₁, \chi₂, S₁, S₂, C₁, C₂$} \] \[ \chi = \chi₁ \cup \chi₂ \cup \{X\} \qquad C = C₁ \cup C₂ \cup \{S₁ = S₂ \to X\}\]
根据 inversion lemma,有 \( \sigma \Gamma \vdash \sigma t₁ : T₁ \to T \) 且 \( \sigma \Gamma \vdash \sigma t₂ : T₁ \)。
根据归纳假设,存在 \( (\sigma₁, T₁) \) 是 \( (\Gamma, t₁, S₁, C₁) \) 的解且 \( \sigma₁ ∖ \chi₁ = \sigma \),且存在 \( (\sigma₂, T₂) \) 是 \( (\Gamma, t₂, S₂, C₂) \) 的解,且 \( \sigma₁ ∖ \chi₁ = \sigma₂ ∖ \chi₂ = \sigma \)。
下面构造 \( \sigma’ \) 使得它满足下面几个条件:\( \sigma’ \setminus \chi = \sigma \);\( \sigma’ X = T \);\( \sigma’ \) unifies \( C₁, C₂ \);\( \sigma’ \) unifies \( \{S₁ = S₂ \to X\} \):
\[\sigma’ = \begin{cases} Y \mapsto U, &\text{if $Y \notin \chi$ and $(Y \mapsto U) \in \sigma$} \\ Y₁ \mapsto U₁, &\text{if $Y₁ \in \chi₁$ and $(Y₁ \mapsto U) \in \sigma₁$} \\ Y₂ \mapsto U₂, &\text{if $Y₂ \in \chi₂$ and $(Y₂ \mapsto U) \in \sigma₂$} \\ X \mapsto T, &\text{else} \end{cases}\]
此处前两个条件显然满足,第三个条件由于 \( \chi₁ \cap \chi₂ = \chi₁ \cap FV(T₂) = \chi₂ \cap FV(T₁) = \emptyset \) 因此也满足,所以只要考虑最后一个条件:不难发现 \( FV(S₁) \cap (\chi₂ \cup \{X\}) = \emptyset \),因此 \( \sigma’ S = \sigma₁ S₁ \),因此 \( \sigma’ S₁ = \sigma₁ S₁ = T₁ \to T = \sigma₂ S₂ \to T = \sigma’S₂ \to \sigma’ X = \sigma’ (S₂ \to X) \) 成立。
其他情况类似。
Suppose \( \Gamma \vdash t : S \mid C \). There is some solution for \( (\Gamma, t) \) iff there is some solution for \( (\Gamma, t, S, C) \).
根据 soundness 和 completeness 得证。
gensym and ML Implementation
在实际的编译器中,会使用一个 gensym 函数修改全局变量来生成新的类型变量。由于这个函数会有全局副作用,因此难以形式化,但是可以用一个新名字的无穷序列来模拟这种行为:令 \( F \) 表示一个包含不同类型变量名字的序列,然后将类型规则写作 \( \Gamma \vdash_F t:T \mid_{F’} C \),其中 \(\Gamma, F, t \) 是算法的输入, \( T, F’, C \) 是算法的输出。当需要新名字时,会直接使用 \( F \) 头部的名字,然后将其从 \( F \) 中移除得到 \( F’ \)。
对应的类型规则如下:
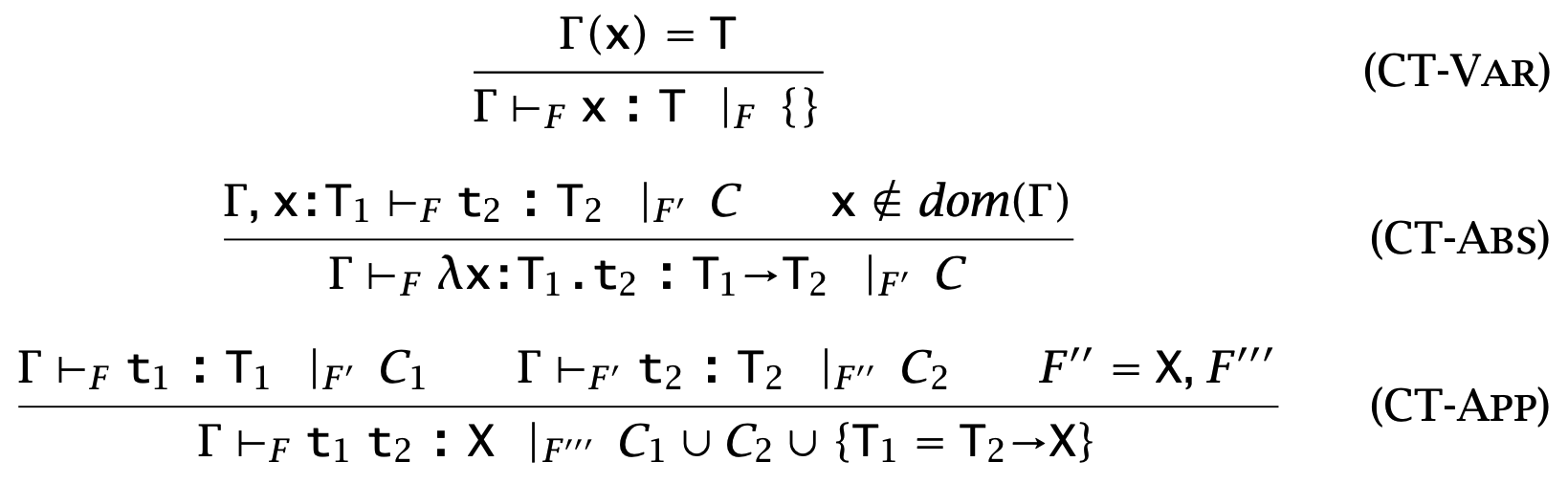
Figure 2: Constraint Typing Rules with gensym
(Soundness)
If \(\Gamma \vdash_F t T \mid_{F’} C\) and the variables mentioned in \(t\) do not appear in \(F\), then \(\Gamma \vdash t: T \mid_{F \setminus F’} C\).
(Completeness)
If \(\Gamma \vdash t: T \mid_\chi C\), then there is some permutation \(F\) of the names in \(\chi\) such that \(\Gamma\vdash_F t : T \mid_\emptyset C\).
Fix
fix 对应的 constraint typing 规则如下:
\[\dfrac{ \Gamma \vdash t₁ : T₁ \mid C₁ \qquad \text{$X$ not mentioned in $\chi₁$, $\Gamma$ or $t_1$} }{ \Gamma \vdash \operatorname{\mathtt{fix}}\ t₁ : X \mid_{\chi₁ \cup \{X\}} C₁ \cup \{T₁ = X \to X\} } \tag{CT-Fix}\]
Unification
\begin{algorithm} \caption{Unification Algorithm} \begin{algorithmic} \procedure{unify}{$C$} \if{$C = \emptyset$} \return{$[]$} \else \state Split $C$ into $\{S = T\}$ and $C’$ \match { (S, T) } \case{ ($t, t$) } \return{$\operatorname{unify}(C’)$} \endcase \case{ $(X, t) \mid (t, X)$ } \if{$X \notin \operatorname{FV}(t)$} \return{$\operatorname{unify}([X \mapsto t]C’) \circ [X \mapsto t]$} \else \state $\operatorname{\mathtt{fail}}$ \endif \endcase \case{ $(S₁ \to S₂, T₁ \to T₂)$ } \return{$\operatorname{unify}(C’ \cup \{S₁ = T₁, S₂ = T₂\})$} \endcase \otherwise \state $\operatorname{\mathtt{fail}}$ \endmatch \endif \endprocedure \end{algorithmic} \end{algorithm}
这个算法不仅可以用于类型系统的 unification,可以用于任何一阶逻辑的 unification 问题。
算法中出现的 \( X \notin FV(T) \) 与 \( X \notin FV(S) \) 称为 occurs check,用于避免出现循环替换(例如 \( X \mapsto X \to X \)),因为这样的表达式只有在 recursive types 中才有意义。
算法主要处理了三种情况:
- \( t = t \) 直接跳过;
- \( X = t \) 或 \( t = X \) 替换
- \( C(a₁, a₂, \dots, aₙ) = C(b₁, b₂, \dots, bₙ) \) 生成新约束并递归求解
- 其他情况返回失败
(More General / Less Specific)
A substitution \( \sigma \) is less specific (or more general) than a substitution \( \sigma’ \), written \( \sigma \sqsubseteq \sigma’ \), if \( \sigma’ = \gamma \circ \sigma \) for some substitution \( \gamma \).
(Principal Unifier)
A principal unifier (or most general unifier) for a constraint set \( C \) is a substitution \( \sigma \) that satisfies \( C \) and such that \( \sigma \sqsubseteq \sigma’ \) for every substitution \( \sigma’ \) satisfying \( C \).
The algorithm unify always terminates, failing when given a non-unifiable constraint set as input and otherwise returning a principal unifier. More formally:
- \( \operatorname{\mathtt{unify}}( C) \) halts, either by failing or by returning a substitution, for all \( C \);
- If \( \operatorname{\mathtt{unify}}( C) = \sigma \), then \( \sigma \) is a unifier for \( C \).
- If \( \delta \) is a unifier for \( C \), then \( \operatorname{\mathtt{unify}}( C) = \sigma \) with \( \sigma \sqsubseteq \delta \). (That is, the algorithm returns a principal unifier.)
首先证明第一条 termination,定义 constraint set \( C \) 的 degree 为 \( (m, n) \),其中 \( m \) 表示 \( C \) 中不同类型变量的数量,\( n \) 表示 \( C \) 中所有类型的总 size。可以证明 \( (m, n) \) 是递减的。
然后证明第二条 correctness。对递归层数进行归纳,其中 \( S = T \) 和 \( S = S₁ \to S₂ \) 的情况比较直观。对于 \( S = X \) 和 \( T = X \) 的情况,只要证明如果 \( \sigma \) unifies \( [X \mapsto T] D \),那么 \( \sigma \circ [X \mapsto T] \) unifies \( \{X = T\} \cup D \) 即可。
最后证明第三条 principal unifier。同样对递归层数进行归纳。
- 如果 \( C = \emptyset \),那直接返回 \( [] \)。由于 \( \delta = \delta \circ [] \),因此 \( [] \sqsubseteq \delta \)
- 如果 \( C \ne \emptyset \) 且 \( C = (S, T) + C’ \)
\( S = T \)。根据归纳假设,设 \( \operatorname{\mathtt{unify}}( C) = \operatorname{\mathtt{unify}}(C’) = \sigma’ \) 则对于任何 \( \delta’ \) unifies \( C’ \) 有 \( \sigma’ \sqsubseteq \delta’ \)。又由于 \( \delta \) unifies \( C \),有 \( \delta \) unifies \( C’ \),因此有 \( \operatorname{\mathtt{unify}}( C) = \sigma’ \sqsubseteq \delta \)。
\( S = X \land X \notin FV(T) \)。由于 \( \delta \) unifies \( S \) 与 \( T \),因此有 \( \delta(S) = \delta(X) = \delta(T) \)。因此对于任意类型 \( U \),有 \( \delta(U) = \delta([X \mapsto T]) U \)。推广可知 \( \delta \) unifies \( [X \mapsto T] C’ \)。
根据归纳假设,设 \( \operatorname{\mathtt{unify}}([X \mapsto T]C’) = \sigma’ \),则有 \( \sigma’ \) 是 principal unifier。由于 \( \delta \) unifies \( [X \mapsto T] C’ \),因此\( \exists \gamma. \delta = \sigma’ \circ \gamma \)。
由于 \( \operatorname{\mathtt{unify}}( C) = \sigma’ \circ [X \mapsto T] \),因此只要证明 \( \delta = \gamma \circ (\sigma’ \circ [X \mapsto T]) \) 即可。考虑一个类型变量 \( Y \),有两种情况:
- 如果 \( X \ne Y \),则 \( (\gamma \circ (\sigma’ \circ [X \mapsto T]))Y = (\gamma \circ \sigma’)Y = \delta Y \),成立。
- 如果 \( X = Y \),则 \( (\gamma \circ (\sigma’ \circ [X \mapsto T]))X = (\gamma \circ \sigma’)T = \delta T = \delta X \),成立。
- 综上,\( \delta = \gamma \circ (\sigma’ \circ [X \mapsto T]) \)。
\( T = X \wedge X \notin FV(S) \) 类似
\( S = S₁ \to S₂ \wedge T = T₁ \to T₂ \),显然。
Principal Types
(Principal Solution)
A principal solution for \((\Gamma, t, S, C)\) is a solution \((\sigma, T)\) such that, whenever \((\sigma’, T’)\) is also a solution for \((\Gamma, t, S, C)\), we have \(\sigma \sqsubseteq \sigma’\).
When \((\sigma, T)\) is a principal solution, we call \(T\) a principal type of \(t\) under \(\Gamma\).
(Principal Types)
If \((\Gamma, t, S, C)\) has any solution, then it has a principal one.
The Unification Algorithm can be used to determine whether \((\Gamma, t, S, C)\) has a solution and to calculate a principal one.
It is decidable whether \( (\Gamma , t) \) has a solution under STLC.
目前的算法会先生成所有约束,然后进行 unification。而由于 unification 的每一步都能保证生成的是 principal type,即每一步都保证生成最紧凑的结果,因此这两部分可以交替增量进行,并且不会影响最后的结果。这样做的优点在于能够更好地报错。
Handle Records
将 unification (在不引入 subtyping 的前提下)拓展到 records 并不平凡。一个简单的尝试是
\[\dfrac{\Gamma \vdash t : T \mid_\chi C}{\Gamma \vdash t.l : X \mid_{\chi \cup \{X\}} C \cup \{T = \{lᵢ : X\}\}}\]
但是这样写只考虑了单 field 的 records 的情况。一个更优雅的方案是 row variable,其作用于 field label 对应的 row,而不是 type:
\[ \dfrac{\Gamma \vdash t₀ : T \mid_\chi C}{\Gamma \vdash t₀.lᵢ : X \mid_{\chi \cup \{X, \sigma, \rho\}} C \cup \{T = \{\rho\}, \rho = l_i : X \oplus \sigma\}} \tag{CT-Pro} \]
此处 \( \sigma \) 和 \( \rho \) 是 row variable,\( \oplus \) 满足结合律和交换律,用于组合两行(假设两部分的 fields 互斥)。因此上面的规则表明当 \( t \) 具有包含 field \( l_i : X \) 和其他 fields \( \sigma \) 的 record type \( \rho \) 时,项 \( t.lᵢ \) 的类型为 \( X \)。但是 row type 生成的规则更复杂,需要 equational unification 来求解。
Implicit Type Annotations
支持 type reconstruction 的语言允许程序员完全省略 lambda abstrations 中的 type annotations。这样的实现一种方法是前面提到的,在 parsing 时添加类型注解,另一种方法是将这种 term 直接纳入语言的语法中,并为其添加类型规则:
\[ \frac{X \notin \chi \qquad \Gamma, x:X \vdash t₁ : T \vert_\chi C}{\Gamma \vdash \lambda x.t₁ : X \to T \vert_{X \cup \chi} C} \tag{CT-AbsInf} \]
这两种做法有一些微妙的区别:如果将 lambda abstraction 复制多份使用,那么第一种方法会导致每个 lambda abstraction 的类型都相同,而 CT-AbsInf 允许每份拷贝有不同的类型,这将引出下面的 let-polymorphism。
Let Polymorphism and Hindley-Milner Type System
多态性(Polymorphism) 是一种程序机制,其使得一部分代码在不同的上下文中不同的类型下使用,从而达到复用的目的。前面展示的类型重建算法提供了一种实现多态的方法,它使得在 let-bound 中绑定的隐式标注的 lambda-abstractions 在不同的类型下被重用,称为 let-polymorphism(也可以叫做 ML-style 或者 Damas-Milner polymorphism)。包含 let-polymorphism 的 STLC 也称为 hindley-milner type system,Algorithm W 是 HM 系统中最知名的类型推导算法。
下面是 let-polymorphism 的一个例子:
let double = λ f: X -> X. λa: X. f(f(a)) in
let a = double (λx:Nat. succ (succ x)) 1 in
let b = double (λx:Bool. x) false in ...
如果想要复用这里的 double,使它能接受 Nat -> Nat 和 Bool -> Bool,那会出现无法 unify 的情况。为了能够复用代码,我们希望 double 每次绑定都关联不同的变量 \( X \)。为此,需要改变类型推断规则。
考虑之前的 T-Let 规则:
\[\dfrac{ \Gamma \vdash t₁ :T₁ \qquad \Gamma, x:T₁ \vdash t₂ : T₂ }{ \Gamma \vdash \operatorname{\mathtt{let}}\ x = t₁\ \operatorname{\mathtt{in}}\ t₂ : T₂ } \tag{T-Let}\]
在原来的规则中,需要先计算 \( t₁ \) 的类型,然后将其绑定到 \( x \) 上并计算 \( t₂ \) 的类型。为了支持 let-polymorphism,我们需要直接在条件中完成替换:
\[\dfrac{ \Gamma \vdash [x \mapsto t₁]t₂ : T₂ }{ \Gamma \vdash \operatorname{\mathtt{let}}\ x = t₁\ \operatorname{\mathtt{in}}\ t₂ : T₂ } \tag{T-LetPoly}\]
\[ \dfrac{ \Gamma \vdash [x \mapsto t₁] t₂ : T₂ \mid_\chi C }{ \Gamma \vdash \operatorname{\mathtt{let}}\ x = t₁\ \operatorname{\mathtt{in}}\ t₂ : T₂ \mid_\chi C } \tag{CT-LetPoly} \]
这样做本质上是在类型推导中提前完成了一步 evaluation。
然后利用上一节提到的 CT-AbsInf 来重写函数,这样就会在求值时使用不同的副本:
let double = λ f. λa. f(f(a));
Unused Bindings
这种方案有一个问题:如果绑定的变量没有在方法体內使用,那绑定的表达式将不会被检查:
let x = <utter garbage> in 5
此处的 <utter garbage> 不会被检查,因为它没有被使用。为了解决这个问题,可以在 premise 中添加一个规则:
\[ \dfrac{ \Gamma \vdash [x \mapsto t₁]t₂ : T₂ \qquad \Gamma \vdash t₁ : T₁ }{ \Gamma \vdash \operatorname{\mathtt{let}}\ x = t₁\ \operatorname{\mathtt{in}}\ t₂ : T₂ } \tag{T-LetPoly’} \]
\[ \dfrac{ \Gamma \vdash [x \mapsto t₁]t₂ : T₂ \mid_\chi C \qquad \Gamma \vdash t₁ : T₁ }{ \Gamma \vdash \operatorname{\mathtt{let}}\ x = t₁\ \operatorname{\mathtt{in}}\ t₂ : T₂ \mid_\chi C } \tag{CT-LetPoly’} \]
Type schemes and Algorithm W
上面的方案的另一个问题是:在 body 中多次使用绑定的变量时,每次出现都需要重新计算绑定 \( t₁ \) 的类型。在原来的方案中,只需要检查两件事:\( t₁ \) 的类型,以及将 \( t₁ \) 加上 context 后 \( t₂ \) 的类型。但是更改后的方案将 \( t₂ \) 中所有的 \( x \) 替换为 \( t₁ \),如果出现 let 绑定时多重嵌套,那么这个检查的复杂度将会是指数级的:
let a = <complex code> in
let b = a + a in
let c = b + b in
let d = c + c in
...
例如此处最后会展开成指数个 <complex code> 的类型推导。
为了避免这个问题,支持 let-polymorphism 的语言采用了另一种做法。对于 \( \operatorname{\mathtt{let}}\ x=t₁\ \operatorname{\mathtt{in}}\ t₂ \),其求解过程如下:
- 使用 constraint typing 算法计算出 \( t₁ \) 对应的类型变量 \( S₁ \) 和约束集合 \( C₁ \);
- 使用 unification 算法找到 \( C₁ \) 的 principal solution \( \sigma \),并得到 principal type \( \sigma \Gamma \vdash \sigma S = T₁ \);
- 将 \( T₁ \) 中的所有类型变量泛化(generalize)。如果剩下的类型变量是 \( X₁, X₂, \dots Xₙ \),那么将其写作 \( \forall X₁ \dots Xₙ. T₁ \) 作为 principal type scheme;
- 这里需要注意不要泛化在 context 中出现的变量,因为他们实际上对应了一个类型约束。例如 \( \lambda f: X \to X. \lambda x: X. \operatorname{\mathtt{let}}\ g = f\ \operatorname{\mathtt{in}}\ g(x) \),这里不应该泛化 \( X \);
- 在 context 中记录 type scheme \( x : \forall X₁ \dots Xₙ. T₁ \),并且开始检查 body \( t₂ \)。此时上下文会给每个自由变量关联一个 type scheme 而非单纯 type。
- 每次在 body 中遇到 \( x \) 时,先查找其 type scheme \( \forall X₁ \dots Xₙ. T₁ \),然后生成新的类型变量 \( Y₁ \dots Yₙ \) 并用它们实例化 type scheme,从而得到 \( [X₁ \mapsto Y₁, \dots, Xₙ \mapsto Yₙ] T₁ \) 作为 \( x \) 的类型。
这就是 Algorithm W。Algorithm W 一般是线性的,但是其最坏复杂度仍然是指数级的:
let f0 = fun x → (x, x) in
let f1 = fun y → f0(f0 y) in
let f2 = fun z → f1(f1 z) in
f2 (fun a → a)
观察这个例子,其中:
- \( f₀ : \forall X. (X, X) \)
- \( f₁ : \forall Y. ((Y, Y), (Y, Y)) \)
- \( f₂ : \forall Z. (((Z, Z), (Z, Z)), ((Z, Z), (Z, Z))) \)
不难发现之所以算法在这里是指数级,是因为这个结果的长度就是指数级。
Side-effects
最后需要注意的一点是,需要小心设计 let-polymorphism 与副作用之间的交互。例如下面这个例子:
let r = ref (λx. x) in
(r := (λx:Nat. succ x); (!r)true);
使用前面的算法可以得出 let-clause 绑定的类型为 \( \operatorname{\mathtt{Ref}}(X \to X) \)。由于 \( X \) 没在上下文中出现,因此可以将其泛化为 type scheme \( \forall X. \operatorname{\mathtt{Ref}}(X \to X) \)。在两处使用中会分别将其实例化为 \( \operatorname{\mathtt{Ref}}(\operatorname{\mathtt{Nat}} \to \operatorname{\mathtt{Nat}}) \) 和 \( \operatorname{\mathtt{Ref}}(\operatorname{\mathtt{Bool}} \to \operatorname{\mathtt{Bool}}) \)。这样的设计是不安全的,因为它会将 \( \operatorname{\mathtt{succ}} \) 作用在 \( \operatorname{\mathtt{true}} \) 上。
这里的问题在于类型规则和求值规则不一致。原来的规则会先将 let-bound 的变量化简为一个值,然后进行替换;而前面引入的类型推导规则会在遇到 let 表达式时立刻进行替换(一步求值)。因此在类型推导中调用了两次 ref,而在运行时只分配了一个 ref。
为了处理这个问题,要么需要调整类型推导规则,要么需要调整求值规则。
前者的做法是:
\[ \operatorname{\mathtt{let}}\ x = t₁\ \operatorname{\mathtt{in}}\ \operatorname{\mathtt{t₂}} \mid \mu \longrightarrow [x \mapsto t₁]t₂ \mid \mu \tag{E-Let} \]
这样调整规则后,原来的表达式会变成
(ref (λx. x)) := (λx:Nat. succ x) in
(!(ref (λx. x))) true;
这为每一处调用都创建了不同的 ref,显然是安全的,但是这种语义不再是 call-by-value 的。
另一种做法是调整类型规则,对其加限制,称为值限制(value restriction):let-bound 只有在其右侧是一个 syntactic value(包括 constants、variables、lambda abstractions 和 application of constructors 等,但不包括 Ref)时才是多态的(即才能被泛化)。上面的程序由于不满足这个条件,因此不会被泛化,所以会报错。
Value restriction 避免了安全性问题,但是同时也牺牲了表达能力。具体什么是允许的,什么是不允许的需要一个个分类讨论,让语言更加复杂。但是实际上这个限制在实践中几乎没有影响,分析发现几乎所有绑定的变量都是 syntactic value,而基于 weak type variables 的 let-typing 只有在极少数情况下才会出现,因此主流的支持 let-polymorphism 的 ML-style 语言都采用了 value restriction。
Let-polymorphism 的问题
上面说明了 let-polymorphism 在处理 side-effects 时遇到了 generalization 的问题,并引入 value restriction 作为解决方案。事实上,let-polymorphism 真正的问题在于 generalization 时放置 \( \forall \) 的位置。
以上面的程序为例:
let r = ref (λx. x) in
(r := (λx:Nat. succ x); (!r)true);
这里 \( r \) 的类型为 \( \forall A. \operatorname{\mathtt{ref}} (A \to A) \) 而不是 \( \operatorname{\mathtt{ref}} (\forall A. A \to A) \),这是 HM 系统推导出来的类型都是 pricipal 的,因为在 generalization 时会直接将 \( \forall \) 放置在右手最外侧。因此引入 value restriction 的根源便在于 generalization 的位置。
那么能不能将其放在 \( \operatorname{\mathtt{ref}} \) 中呢?如果能做到,那么在赋值 (λx: Nat. succ x) 时就会出现错误(因为无法将 Int -> Int 赋值给 r)。但是在下一章 System F 中可以看到,如果允许这么做,那么这个类型系统将是 rank-N polymorphism 的,其上的类型推导是 undecidable 的。因此这是 let-polymorphism 放弃表达力而换取可判定性的结果。
Implementation of Algorithm W
type ty =
TyUnit
| TyArr of ty * ty
| TyMono of string
| TyPoly of string * ty
type term =
TmUnit
| TmVar of string
| TmAbs of string * ty option * term
| TmApp of term * term
| TmLet of string * term * term
(** Ctx *)
type context = (string * ty) list
type constraints = (ty * ty) list
let getTypeFromContext ctx name =
try Some (List.assoc name ctx)
with Not_found -> None
(** New Variable Generator*)
let fresh =
let i = ref 0 in
fun () ->
let i' = "?X_" ^ (string_of_int !i) in
incr i;
i'
(** Substitution *)
(** [tyX -> tyT] tyS *)
let substTy (tyX : string) tyT tyS =
let rec f = function
TyUnit -> TyUnit
| TyArr(tyS1, tyS2) -> TyArr(f tyS1, f tyS2)
| TyMono(x) -> if x = tyX then tyT else TyMono(x)
| TyPoly(x, tyS) -> if x = tyX
then raise (Failure "Name conflicts with Poly")
else TyPoly(x, f tyS)
in f tyS
(** [tyX1 -> tyT1]...[tyXn -> tyTn] tyS *)
let applySubsts substs tyS =
List.fold_left (fun tyS (tyX, tyT) -> substTy tyX tyT tyS)
tyS (List.rev substs)
(** [tyX -> tyT] C *)
let substConstraints (tyX : string) tyT constr =
List.map
(fun (tyS1, tyS2) -> (substTy tyX tyT tyS1, substTy tyX tyT tyS2))
constr
(** [tyX1 -> tyT1]...[tyXn -> tyTn] ctx *)
let substCtx substs ctx =
List.map (fun (x, tyT) -> (x, applySubsts substs tyT)) ctx
(** Unification *)
let occurs (tyX : string) tyT =
let rec o = function
TyUnit -> false
| TyArr(tyT1, tyT2) -> o tyT1 || o tyT2
| TyMono(x) -> x = tyX
| TyPoly(x, tyT1) -> if x = tyX then raise (Failure "Name conflicts with Poly")
else o tyT1
in o tyT
let unify substs =
let rec u = function
[] -> []
| (tyS, tyT) :: rest when tyS = tyT -> u substs
| (tyS, TyMono(x)) :: rest | (TyMono(x), tyS) :: rest ->
if occurs x tyS then raise (Failure "Occurs check")
else List.append (u (substConstraints x tyS rest))
[(x, tyS)]
| (TyArr(tyS1, tyS2), TyArr(tyT1, tyT2)) :: rest ->
u ((tyS1, tyT1) :: (tyS2, tyT2) :: rest)
| _ -> raise (Failure "Unification failed")
in u substs
(** Inference *)
module VarSet = Set.Make(String)
let generalize ctx tyT =
let rec g ctx = function
TyUnit -> VarSet.empty
| TyArr(tyT1, tyT2) -> VarSet.union (g ctx tyT1) (g ctx tyT2)
| TyMono(x) -> if List.mem_assoc x ctx then VarSet.empty else VarSet.singleton x
| TyPoly(x, tyT) -> raise (Failure "Polymorphic type in generalization")
in
let tyVars = g ctx tyT in
VarSet.fold (fun x tyT' -> TyPoly(x, tyT')) tyVars tyT
let instantiate tyS =
let rec f substs tyS = match tyS with
TyPoly(x, tyT) ->
let y = TyMono(fresh ()) in
f ((x, y) :: substs) tyT
| _ -> applySubsts substs tyS
in f [] tyS
let infer t =
let rec infer' ctx = function
TmUnit -> (TyUnit, [])
| TmVar(x) -> (match getTypeFromContext ctx x with
Some(tyT) -> (instantiate tyT, [])
| None -> raise (Failure ("Unbound variable " ^ x)))
| TmAbs(x, tyX, t) ->
let tyX' = (match tyX with
Some(tyX) -> tyX
| None -> TyMono(fresh ())) in
let (tyT, substs) = infer' ((x, tyX') :: ctx) t in
(TyArr(tyX', tyT), substs)
| TmApp(t1, t2) ->
let (tyT1, substs1) = infer' ctx t1 in
let (tyT2, substs2) = infer' ctx t2 in
let tyRet = TyMono(fresh ()) in
let newSubst = [(tyT1, TyArr(tyT2, tyRet))] in
(tyRet, List.concat [substs1; substs2; newSubst])
| TmLet(x, t1, t2) ->
let (tyT1, substs1) = infer' ctx t1 in
let sigmaT1 = unify substs1 in
let scheme = generalize (substCtx sigmaT1 ctx) (applySubsts sigmaT1 tyT1) in
let (tyT2, substs2) = infer' ((x, scheme) :: ctx) t2 in
(tyT2, List.concat [substs1; substs2])
in infer' [] t
(** Pretty print type *)
let pp ty =
let rec f = function
TyUnit -> "Unit"
| TyArr(ty1, ty2) -> "(" ^ (f ty1) ^ " -> " ^ (f ty2) ^ ")"
| TyMono(x) -> x
| TyPoly(x, ty) -> "forall " ^ x ^ ". " ^ (f ty)
in f ty
let ppinfer t =
let (ty, substs) = infer t in
let sigmaT1 = unify substs in
let scheme = generalize (substCtx sigmaT1 []) (applySubsts sigmaT1 ty) in
pp scheme;;
Hindley-Milner 的拓展
- Impredicative polymorphism(System F,下一章讨论):已经被证明是 undecidable 的;
- First-class polymorphism:支持将 polymorphic type 作为参数传递,类似于 System F,但是需要一些显式标注的类型来避免 undecidability;
- Recursive type
- Polymorphism + Recursive type = Polymorphic Recursion,对应的演算称为 Milner-Mycroft Calculus,对应了 semi-unification 问题,也是 undecidable 的;
- 但是如果没有 polymorphism,那么这是 decidable 的;
- Subtyping
- 在 norminal subtyping 中,由于两个类型可能没有一个公共的并,或者有可能有多个公共的并,因此它们也就没有 principal type;
- 在 structural subtyping 中,发展出了 algebraic subtyping,对 subtyping 做出了一些限制,如不允许 union type 出现在函数参数位置;或者 F-sub 这样的系统,在 System F 上做了 subtyping 的拓展,但是它不支持 H-M 风格的类型推断;另一个替代方案是 row polymorphism,针对 records 和 variants 实现了多态,并实现了近似于 subtyping 的效果。