这章介绍基于 equi-recursive 的 typechecker(基于 iso-recursive 的相对来说比较简单),开发一个能够处理 subtyping + recursive types 的 typechecker,并为 equi-recursive 构建数学框架。
Knaster-Tarski Theorem
在讨论之前,需要确定一个 universal set \( \mathcal{U} \),它代表了 everything in the world。而定义 inductive 和 coinductive 是为了从 \( \mathcal{U} \) 提取一个我们关心的子集(后面会将所有类型组成的 pairs 组成的集合作为 \( \mathcal{U} \),这样就能讨论类型之间的关系)。
(Monotone)
A function \( F \in \mathcal{P}(\mathcal{U}) \to \mathcal{P}(\mathcal{U}) \) is monotone if \( X \subseteq Y \implies F(X) \subseteq F(Y) \).
(\( \mathcal{P}(\mathcal{U}) \) is the set of all subsets of \( \mathcal{U} \).)
在下面的讨论中假设 \( F \) 是 \(\mathcal{P}(\mathcal{U})\) 的单调(monotone)函数,也被称为生成函数(generating function)。
Let \( X \) be a subset of \( \mathcal{U} \).
- \( X \) is \( F \)-closed if \( F(X) \subseteq X \).
- \( X \) is \( F \)-consistent if \( X \subseteq F(X) \).
- \( X \) is a fixed point of \( F \) if \( F(X)=X \).
可以看出 fixed-point 是一个既 closed 又 consistent 的集合。
一个有趣的角度是将 \( U \) 看作断言的集合,将 \( F \) 看作一个证明关系:它对于给定的断言,能推理出新的断言。因此:
- 一个 \( F \)-closed 的断言集合包含了所有能证明的结论
- 一个 \( F \)-consistent 的断言集合能“自我证明”:集合中的每个断言都能通过集合中的其他断言推导出来
- 一个 fixed-point 是一个既能证明自己、又包含所有能证明的结论的集合
(Knaster-Tarski Theorem)
- The intersection of all \( F \)-closed sets is the least fixed point of \( F \).
- The union of all \( F \)-consistent sets is the greatest fixed point of \( F \).
这里只证明第二部分,第一部分的证明类似。
设 \( C = \{ X | X \subseteq F(X) \} \) 是所有 \( F \)-consistent 集合的集合,令 \( P = ⋃ C \)。
由于 \( F \) 是单调的,且 \( X \subseteq P \),因此有 \( F(X) \subseteq F(P) \)。根据传递性有 \( X \subseteq F(P) \)。
因此 \( P = \bigcup_{X \in C} X \subseteq F(P) \),即 \( P \) 是 \( F \)-consistent 的。并且根据定义,\( P \) 是最大的 \( F \)-consistent 集合。
再次利用 \( F \) 的单调性,有 \( F(P) \subseteq F(F(P)) \),即 \( F(P) \) 也是 \( F \)-consistent 的,因此 \( F(P) \in C \)。根据 \( P \) 的定义,有 \( F(P) \in C \subseteq P \),因此 \( P \) 是 \( F \)-closed 的。因此 \( P \) 是 \( F \) 的 fixed-point。
由于 \( P \) 是最大的 \( F \)-consistent 集合,因此 \( P \) 是 \( F \) 的最大 fixed-point。
(\( \mu \) and \( \nu \))
The least fixed point of \( F \) is written \( \mu F \).
The greatest fixed point of \( F \) is written \( \nu F \).
Corollaries
Knaster-Tarski 定理的一个推论是,对于 \( F \) 必定存在 \( \mu F \) 和 \( \nu F \)(可能相等):
[of Knaster-Tarski Theorem]
- \( \mu F \) exists.
- \( \nu F \) exists.
根据 Knaster-Tarski 定理,只要证明在 \( \mathcal{U} \) 上一定存在 \( F \)-closed 和 \( F \)-consistent 的集合即可。
\[F(\mathcal{U}) \subseteq \mathcal{U}\]
\[\emptyset \subseteq F(\emptyset)\]
因此 \( \emptyset \) 是 \( F \)-consistent 的。而 \( \mathcal{U} \) 是 \( F \)-closed 的。
Kleene fixed-point theorem, [of Knaster-Tarski Theorem]
- \( \mu F = \bigcup \{F^{n}(\emptyset) \mid n \ge 0\} = F(\emptyset) \cup F(F(\emptyset)) \cup F(F(F(\emptyset))) \dots \)
- \( \nu F = \bigcap \{F^{n}(\mathcal{U}) \mid n \ge 0\} = F(\mathcal{U}) \cap F(F(\mathcal{U})) \cap F(F(F(\mathcal{U}))) \dots\)
由于对偶性,这里只证明第二部分。记 \( A = \bigcap \{F^{n}(\mathcal{U}) \mid n \ge 0\} \),要证明 \(\nu F = A\),只要证明 \( A \subseteq \nu F \) 且 \( \nu F \subseteq A \)。
首先证明 \( A \subseteq \nu F \),只要证明 \( A \subseteq F(A) \)。下面首先证明有 \( \mathcal{U} \supseteq F(\mathcal{U}) \supseteq F(F(\mathcal{U})) \supseteq \dots \)。
- 当 \( n = 0 \) 时,有 \( \mathcal{U} \supseteq F(\mathcal{U}) \) 显然成立
- 设当 \( n = k \) 时,有 \( F^{k}(\mathcal{U}) \supseteq F^{k + 1}(\mathcal{U}) \) 成立。当 \( n = k + 1 \) 时,根据单调性有 \( F(F^{k}(\mathcal{U})) \supseteq F(F^{k + 1}(\mathcal{U})) \),即 \( F^{k+1}(\mathcal{U}) \supseteq F^{k + 2}(\mathcal{U}) \)。
因此有:
\[ F(A) = F(\bigcap \{F^{n}(\mathcal{U}) \mid n \ge 0\}) = \bigcap \{F(F^{n}(\mathcal{U})) \mid n \ge 0\} = \bigcap \{F^{n}(\mathcal{U}) \mid n \ge 1\} \cap \mathcal{U} = A \]
然后证明 \( \nu F \subseteq A \)。由于 \( \nu F = \bigcup \{B \mid \text{$B$ is $F$-consistent}\} \),因此只要证明任取 \( F \)-consistent 的集合 \( B \),对于任意的 \( n \) 有 \( B \subseteq R^{n}(\mathcal{U}) \)。对 \( n \) 进行归纳:
- 当 \( n = 0 \) 时,\( B \subseteq F^{0}(\mathcal{U}) = \mathcal{U} \) 显然成立
- 设当 \( n = k \) 时,有 \( B \) 有 \( B \subseteq F^{k}(\mathcal{U}) \) 成立。当 \( n = k + 1 \) 时,根据单调性有 \( F(B) \subseteq F(F^{k}(\mathcal{U})) \)。又由于 \( B \subseteq F(B) \),因此有 \( B \subseteq F(F^{k}(\mathcal{U})) = F^{k + 1}(\mathcal{U}) \)。
- 综上,对于任意 \( n \) 有 \( B \subseteq F^{n}(\mathcal{U}) \),因此 \( \nu F \subseteq A \)。
Induction and Coinduction
注意到 \( \mu F \) 是最小的 \( F \)-closed 集合,而 \( \nu F \) 是最大的 \( F \)-consistent 集合。有下面的推论:
[of Knaster-Tarski Theorem]
- Principle of induction: If \( X \) is \( F \)-closed, then \( \mu F \subseteq X \).
- Principle of coinduction: If \( X \) is \( F \)-consistent, then \( X \subseteq \nu F \).
- \( \forall X\ (X = F(X)).\mu F \subseteq X \subseteq \nu F \)
如果将 \( X \) 看作一个 predicate,那么 predicate 可以由它的特征集合(\( \mathcal{U} \) 的子集中令 predicate 为真的集合)来表示。要证明属性 \( X \) 对元素 \( x \) 成立,相当于证明 \( x \in X \)。
Principle of induction 表明,如果属性 \( X \) 在 \( F \) 下保持(即该属性是 \( F \)-closed 的),那么它对 inductively defined 的集合 \( \mu F \) 中的所有元素都成立。
而 principle of coinduction 则提供了一种确定元素 \( x \) 是否属于 coinductively defined 的集合 \( \nu F \) 的方法:要证明元素 \( x \in \nu F \),只需要找到一个在 \( F \) 下保持的属性 \( X \),并使得 \( x \in X \)。它是许多理论的基础。
利用这两条推论,可以证明自然数上的归纳原理:
(Principle of ordinary induction on natural numbers)
Suppose that \( P \) is a predicate on the natural numbers. Then:
If \( P(0) \) and, for all \( i \) \( P(i) \) implies \( P(i + 1) \), then \( P(n) \) holds for all \( n \).
定义 \( F: \mathcal{P}(\mathbb{N}) \to \mathcal{P}(\mathbb{N}), F(X) = \{0\} \cup \{ i + 1 | i \in X \} \)。
一个 predicate \( P \) 可以用一个集合表示。设 \( P(0) \) 成立(即 \( 0 \in P \))并且 \( \forall i. P(i) \implies P(i + 1) \)(即 \( \forall i. i \in P \implies i + 1 \in P \))。根据 \( F \) 的定义,\( X \subseteq P \implies F(X) \subseteq P \),因此 \( P \) 是 \( F \)-closed 的。因此根据 principle of induction,有 \( \mu F \subseteq P \)。
而 \( \mu F = \mathbb{N} \),因此 \( P \) 包含了所有自然数,即 \( P(n) \) 对所有 \( n \) 成立。
下面将用 greatest fixed points 和 coinductive proof method 来处理 subtyping。
Membership Checking
\( \operatorname{\mathtt{support}} \)
本章将解决这样一个问题:对于给定的 universe \( U \) 和生成函数 \( F \),考虑 \( x \in \mathcal{U} \),判定 \( x \) 是否属于 \( \nu F \)(判断 \( \mu F \) 比较简单)。
对于给定元素,可能存在多个集合 \( X \subseteq U \) 使得 \( x \in F(X) \)。我们将满足条件的集合 \( X \) 称为 \( x \) 的生成集(generating set)。由于 \( F \) 的单调性,\( x \) 的生成集的超集也是 \( x \) 的生成集,因此我们可以只考虑 \( x \) 的最小生成集。
(invertible)
A generating function \( F \) is said to be invertible if, for all \( x \in \mathcal{U} \), the collection of sets
\[ G_x = \{ X \subseteq U \mid x \in F(X) \} \]
either is empty or contains a unique member that is a subset of all the others.
When \( F \) is invertible, the partial function \( \operatorname{\mathtt{support}}_F \in \mathcal{U} \rightharpoonup P(U) \) is defined as follows:
\[\operatorname{\mathtt{support}}_F (x) = \begin{cases} X & \text{if $X \in G_x$ and $\forall X’ \in G_x . X \subseteq X’$} \\ \uparrow & \text{if $G_x = \emptyset$} \end{cases}\]
The support function can be lifted to sets:
\[\operatorname{\mathtt{support}}_F (X) = \begin{cases} \bigcup_{x \in X}\operatorname{\mathtt{support}}_F(x) & \text{if $∀ x \in X. \operatorname{\mathtt{support}}_F(x) \downarrow$} \\ \uparrow & \text{otherwise} \end{cases}\]
这里 \( \uparrow \) 表示未定义,\( \downarrow \) 表示存在定义。
对于 invertible generating function,每个元素 \( x \) 只有一种生成方式,这样追溯上去就只会有一条路径,否则会出现组合路径爆炸的问题。
An element \( x \) is \( F \)-supported if \( \operatorname{\mathtt{support}}_F (x) \downarrow \); otherwise, \( x \) is \( F \)-unsupported.
An \( F \)-supported element is called \( F \)-ground if \( \operatorname{\mathtt{support}}_F(x) = \emptyset \).
- 对于一个 unsupported 的元素 \( x \),\( \forall X \subseteq \mathcal{U}. x \notin F(X) \)
- 对于一个 ground 的元素 \( x \),\( \forall X \subseteq \mathcal{U}. x \in F(X) \)
Invertible function 可以被表示成一个 support graph,图上的每个节点是一个元素,边 \( x \to y \) 表示 \( y \in \operatorname{\mathtt{support}}_F(x) \),即需要 \( y \) 来生成 \( x \)。
例如在下面的 support graph 中有 \( \dfrac{i \quad a}{h} \),\( \dfrac{}{g} \) 等。图中 \( i \) 是 unsupported 的,\( g \) 是 ground 的;注意这里 \( h \) 虽然依赖于 \( i \) 生成,但是 \( h \) 本身是 supported 的。
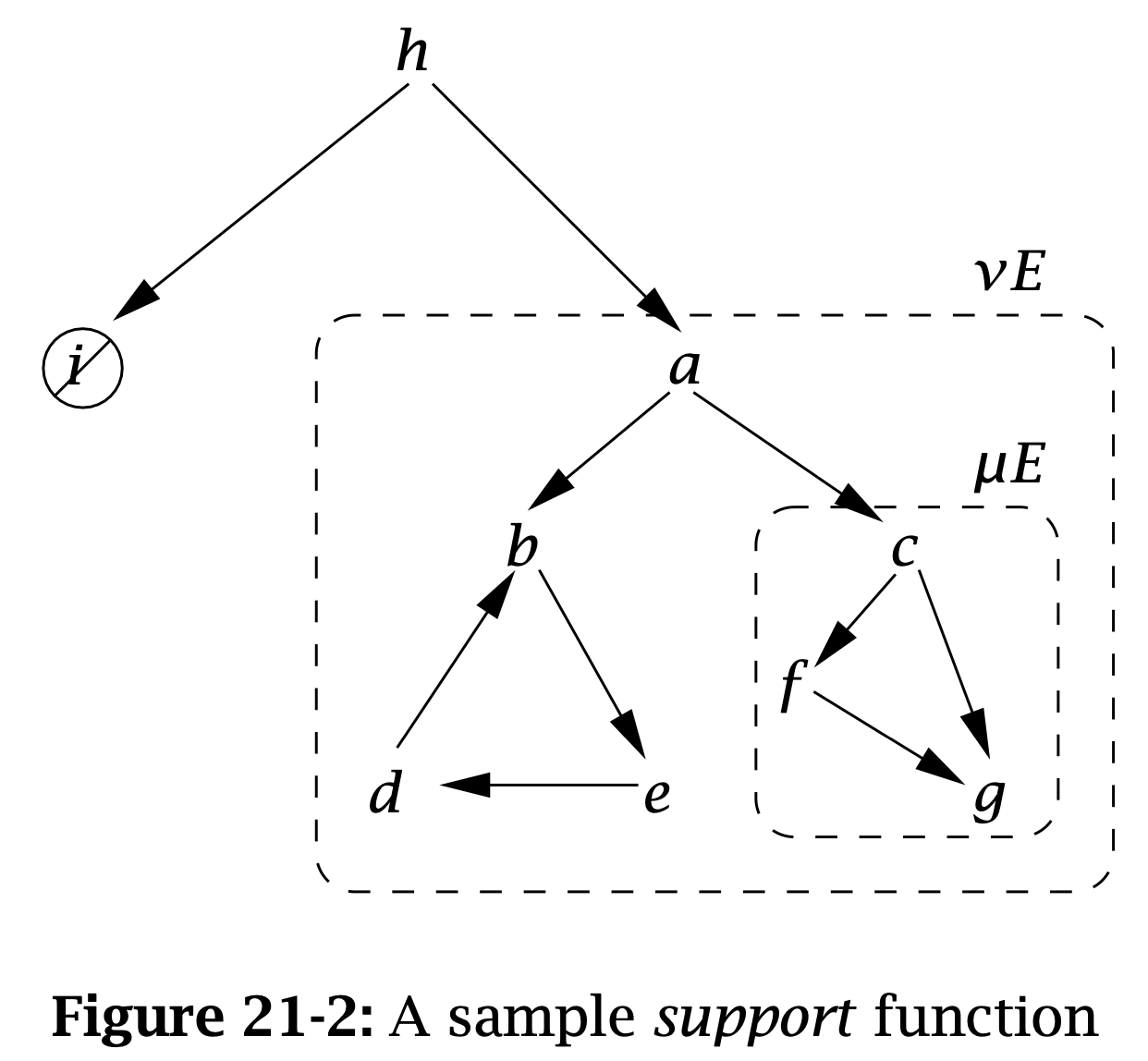
Figure 1: 21-2-sample-support-function
观察 support graph 可以发现:
- 只有当从 \( x \) 出发无法到任何 unsupported 元素时,才有 \( x \in \nu F \)
- \( \nu F = \bigcap \{F^{n}(\mathcal{U}) \mid n \ge 0\}\) 理解,假设以元素 \( x \) 为起点走 \( n \) 步会到达 unsupported 元素,那么 \( x \notin F^n(\mathcal{U}) \)
- 只有当从 \( x \) 出发无法到任何环或无穷链时,才有 \( x \in \mu F \)
- 可以从 \( \mu F = \bigcup \{F^{n}(\emptyset) \mid n \ge 0\} \) 理解,其中 \( x \in F(\emptyset) \) 是 ground 的元素,\( F^n(\emptyset) \) 中的元素为起点走 \( n \) 步,能保证都停在 ground 元素上
这里值得考虑的一个特殊情况是 \( F(X) = \{0\} \cup \{n \mid n + 1 \in X\} \),有 \( \mu F = \{0\}, \nu F = \mathbb{N} \)。
\( \operatorname{\mathtt{gfp}} \)
(gfp, greatest fixed-point)
Suppose \( F \) is an invertible generating function. Define the boolean-valued function \( \operatorname{\mathtt{gfp}}_F \) as follows:
\begin{aligned} \operatorname{\mathtt{gfp}}(X) = & \operatorname{\mathtt{if}}\ \operatorname{\mathtt{support}}(X) \uparrow\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}} \\ & \operatorname{\mathtt{else}}\ \operatorname{\mathtt{if}}\ \operatorname{\mathtt{support}}(X) \subseteq X\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{true}} \\ & \operatorname{\mathtt{else}}\ \operatorname{\mathtt{gfp}}(\operatorname{\mathtt{support}}(X) \cup X). \end{aligned}
We extend \( \operatorname{\mathtt{gfp}} \) to individual elements by taking \( \operatorname{\mathtt{gfp}}(x) = \operatorname{\mathtt{gfp}}(\{x\}) \).
下面将证明 \( \operatorname{\mathtt{gfp}} \) 的正确性和停机性。
Correctness
\[ X \subseteq F(Y) \iff \operatorname{\mathtt{support}}_F(X) \downarrow \land \operatorname{\mathtt{support}}_F(X) \subseteq Y \]
要证明原命题,只要证明
\[ x \in F(Y) \iff \operatorname{\mathtt{support}}_F(x) \land \operatorname{\mathtt{support}}_F(x) \subseteq Y \]
首先证明充分性。设 \( x \in F(Y) \),则 \( Y \in Gₓ \),因此 \( Gₓ \ne \emptyset \)。由于 \( F \) 是 invertible 的,因此 \( \operatorname{\mathtt{support}}_F(x) \uparrow \land \operatorname{\mathtt{support}}_F(x) \subseteq Y \)。
然后证明必要性,如果 \( \operatorname{\mathtt{supprt}}_F(x) \subseteq Y \),那么根据 \( F \) 的单调性有 \( F(\operatorname{\mathtt{support}}_F(x)) \subseteq F(Y) \),又 \( x \in F(\operatorname{\mathtt{support}}_F(x)) \),因此 \( x \in F(Y) \)。
Suppose \( P \) is a fixed point of \( F \), then
\[ X \subseteq P \iff \operatorname{\mathtt{support}}_F(X) \downarrow \land \operatorname{\mathtt{support}}_F(X) \subseteq P \]
\( P = F(P) \),然后代入上一个 lemma 易得。
这里首先证明 gfp 的 partial correctness,然后讨论 termination。
For \( \operatorname{\mathtt{gfp}}_F(X) \),
\(\operatorname{\mathtt{gfp}}_F(X) = \operatorname{\mathtt{true}} \Rightarrow X \subseteq \nu F\)
\(\operatorname{\mathtt{gfp}}_F(X) = \operatorname{\mathtt{false}} \Rightarrow X \not\subseteq \nu F\)
首先证明第一条推论。对 \( \operatorname{\mathtt{gfp}} \) 的递归计算过程进行归纳。在 \( \operatorname{\mathtt{gfp}} \) 的定义中,有两种情况使得其返回 \( \operatorname{\mathtt{true}} \):
- \( \operatorname{\mathtt{support}}(X) \subseteq X \),根据 lemma 有 \( X \subseteq F(X) \),因此 \( X \subseteq \nu F \)
- \( \operatorname{\mathtt{gfp}}(\operatorname{\mathtt{support}}(X) \cup X) = \operatorname{\mathtt{true}}\),根据归纳假设有 \( \operatorname{\mathtt{support}}(X) \cup X \subseteq \nu F \),即 \( X \subseteq \nu F \)。
然后证明第二条推论。同样对 \( \operatorname{\mathtt{gfp}} \) 的递归计算过程进行归纳:
- \( \operatorname{\mathtt{support}}(X) \uparrow \),根据 lemma 有 \( X \not\subseteq \nu F \)
- \( \operatorname{\mathtt{gfp}}(\operatorname{\mathtt{support}}(X) \cup X) = \operatorname{\mathtt{false}} \),根据归纳假设有 \( \operatorname{\mathtt{gfp}}(\operatorname{\mathtt{support}}(X) \cup X) \not\subseteq \nu F \)
- 如果 \( X \not\subseteq \nu F \),原命题成立
- 如果 \( \operatorname{\mathtt{support}}(X) \not\subseteq \nu F \),根据 lemma 有 \( X \not\subseteq \nu F \)
Termination
下面给出一个 termination 的充分条件,用以保证在某类特殊的生成函数下 \( \operatorname{\mathtt{gfp}} \) 能终止。
Given an invertible generating function \( F \) and an element \( x \in \mathcal{U} \), the set \( \operatorname{\mathtt{pred}}_F(x) \) (or just \( \operatorname{\mathtt{pred}}(x) \)) of immediate predecessors of \( x \) is
\[ \operatorname{\mathtt{pred}}_F(x) = \begin{cases} \emptyset, & \text{if $\operatorname{\mathtt{support}}(x) \uparrow$} \\ \operatorname{\mathtt{support}}(x), & \text{if $\operatorname{\mathtt{support}}(x) \downarrow$} \end{cases} \]
and its extension to sets \( X \subseteq \mathcal{U} \) is
\[\operatorname{\mathtt{pred}}(X) = \bigcup_{x \in X} \operatorname{\mathtt{pred}}(x)\]
The set \( \operatorname{\mathtt{reachable}}_F(X) \) (or just \( \operatorname{\mathtt{reachable}}(X) \)) of all elements reachable from a set \( X \) via \( \operatorname{\mathtt{support}} \) is defined as
\[\operatorname{\mathtt{reachable}}(X) = \bigcup_{n \ge 0} \operatorname{\mathtt{pred}}^n(X)\]
and its extension to single elements \( x \in \mathcal{U} \) is
\[\operatorname{\mathtt{reachable}}(x) = \operatorname{\mathtt{reachable}}(\{x\})\]
An element \( y \in \mathcal{U} \) is reachable from an element \( x \) if \( y ∈ \operatorname{\mathtt{reachable}}(x) \).
\( \operatorname{\mathtt{pred}}(x) \) 可以看作 \( x \) 在 support graph 上后继的集合,即 \( \operatorname{\mathtt{support}}(X) \) 递归访问的元素集合。
An invertible generating function \( F \) is said to be finite state if \( \operatorname{\mathtt{reachable}}(x) \) is finite for each \( x \in \mathcal{U} \).
对于一个 finite-state 的生成函数,对 \( \operatorname{\mathtt{support}}(X) \) 递归搜索时,其搜索空间是有穷的,因此 \( \operatorname{\mathtt{gfp}} \) 会终止。
If \( \operatorname{\mathtt{reachable}}_F(X) \) is finite, then \( \operatorname{\mathtt{gfp}}_F(X) \) is defined.
考虑 \( \operatorname{\mathtt{gfp}}(X) \) 递归查询了 \( \operatorname{\mathtt{gfp}}(Y) \),则有 \( Y \subseteq \operatorname{\mathtt{reachable}}(X) \),并且有 \( m(Y) = | \operatorname{\mathtt{reachable}}(X)| - |Y| \) 递减,因此 \( \operatorname{\mathtt{gfp}}(X) \) 会终止。
If \( F \) is finite-state, then \( \forall X \subseteq \mathcal{U} \), \( \operatorname{\mathtt{gfp}}_F(X) \) terminates.
\( \operatorname{\mathtt{lfp}} \)
(lfp, least fixed-point)
Suppose \( F \) is an invertible generating function. Define the function \( \operatorname{\mathtt{lfp}}_F \) (or just \( \operatorname{\mathtt{lfp}} \)) as follows:
\begin{aligned} \operatorname{\mathtt{lfp}}(X) = & \operatorname{\mathtt{if}}\ \operatorname{\mathtt{support}}(X) \uparrow\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}} \\ & \operatorname{\mathtt{else}}\ \operatorname{\mathtt{if}}\ X = \emptyset\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{true}} \\ & \operatorname{\mathtt{else}}\ \operatorname{\mathtt{lfp}}(\operatorname{\mathtt{support}}(X)) \end{aligned}
从直觉上,\( \operatorname{\mathtt{lfp}} \) 会不断向下找,直到所有元素都是 ground 的时 \( \operatorname{\mathtt{lfp}} \) 会返回 true。
For \( \operatorname{\mathtt{lfp}}_F(X) \),
- \( \operatorname{\mathtt{lfp}}_F(X) = \operatorname{\mathtt{true}} \Rightarrow X \subseteq \mu F \)
- \( \operatorname{\mathtt{lfp}}_F(X) = \operatorname{\mathtt{false}} \Rightarrow X \not\subseteq \mu F \)
正确性证明和 \( \operatorname{\mathtt{gfp}} \) 类似。
下面讨论 \( \operatorname{\mathtt{lfp}} \) 的 termination。同理,下面给出一个 termination 的充分条件。
Given a finite-state generating function \( F \in \mathcal{P}(\mathcal{U}) \to \mathcal{P}(\mathcal{U}) \), the partial function \( \operatorname{\mathtt{height}}_F \in \mathcal{U} \rightharpoonup \mathbb{N} \) is the least partial function satisfying:
\[\operatorname{\mathtt{height}}_F(x) = \begin{cases} 0, & \text{if $\operatorname{\mathtt{support}}(x) = \emptyset$ or $\operatorname{\mathtt{support}}(x) \uparrow$} \\ 1 + \max \{ \operatorname{\mathtt{height}}(y) \mid y \in \operatorname{\mathtt{support}}(x) \}, & \text{if $\operatorname{\mathtt{support}}(x) \ne \emptyset$} \end{cases}\]
\( \operatorname{\mathtt{height}}(x) \) is undefined if x either participates in a reachability cycle itself, or depends on an element from a cycle.
\( \operatorname{\mathtt{height}}(X) \) 可以看作 \( X \) 在 support graph 上的不含环的最大高度。
A generating function \( F \) is said to be finite height if \( \operatorname{\mathtt{height}}_F \) is a total function.
If \( F \) is finite-state and finite-height,then \( \operatorname{\mathtt{lfp}} \) terminate for any finite set \( X \subseteq \mathcal{U} \).
不难发现
\[ y \in \operatorname{\mathtt{support}}(x) \land \operatorname{\mathtt{height}}(x) \downarrow \land \operatorname{\mathtt{height}}(y) \downarrow \implies \operatorname{\mathtt{height}}(y) < \operatorname{\mathtt{height}}(x) \]
由于 F 是 finite-state 的,因此递归链有限;由于 F 是 finite-height 的,因此 \( h(Y) = max{height(y) | y ∈ Y} \) 也是 total 的,根据上面的不等式易得 \( h(Y) \) 递减,因此 \( \operatorname{\mathtt{lfp}} \) 会终止。
More Efficient Algorithms
下面给出一系列逐步改进效率的算法。
在递归计算 \( \operatorname{\mathtt{gfp}} \) 时,需要反复计算元素 \( x \) 的 \( \operatorname{\mathtt{support}} \) 并加入集合。这是一个重复计算,因为对于已经计算过的元素 \( x \),肯定有 \( \operatorname{\mathtt{support}}(x) \subseteq X\)。因此每次我们只需要考虑新加入的元素,将集合分为两部分:集合 \( A \) 包含已经计算过 \( \operatorname{\mathtt{support}} \) 的元素,集合 \( X \) 包含新加入的元素。
Suppose \( F \) is an invertible generating function.
Define the function \( \operatorname{\mathtt{gfp}}^a_F \) (or just \( \operatorname{\mathtt{gfp}}^a \)) as follows:
\begin{aligned} \operatorname{\mathtt{gfp}}^a(A, X) = &\operatorname{\mathtt{if}}\ \operatorname{\mathtt{support}}(X) \uparrow\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}}\\ & \operatorname{\mathtt{else}}\ \operatorname{\mathtt{if}}\ X = ∅\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{true}} \\ & \operatorname{\mathtt{else}}\ \operatorname{\mathtt{gfp}}^a(A \cup X, \operatorname{\mathtt{support}}(X) \setminus (A \cup X)) \end{aligned}
In order to check \( x \in \nu F \), compute \( \operatorname{\mathtt{gfp}}^a(\emptyset, \{x\}) \).
这个算法的一个变种是每次只计算一个元素的 \( \operatorname{\mathtt{support}} \):
Suppose \( F \) is an invertible generating function.
Define the function \( \operatorname{\mathtt{gfp}}^s_F \) (or just \( \operatorname{\mathtt{gfp}}^s \)) as follows:
\begin{aligned} \operatorname{\mathtt{gfp}}^s(A, X) = &\operatorname{\mathtt{if}}\ X = ∅\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{true}} \\ & \operatorname{\mathtt{else}}\ \text{let $x$ be some element of $X$ in} \\ & \quad \operatorname{\mathtt{if}}\ x \in A\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{gfp}}^s(A, X \setminus \{x\}) \\ & \quad \operatorname{\mathtt{else}\ if}\ \operatorname{\mathtt{support}}(x) \uparrow\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}} \\ & \quad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{gfp}}^s(A \cup \{x\}, (X \cup \operatorname{\mathtt{support}}(x)) \setminus (A \cup \{x\})) \end{aligned}
仿照前面的证明,可以证明这几个定义的正确性和停机性。
在此基础上可以进一步改进,上面的算法每次都将一个集合作为参数,每次传递的开销非常大,可以用一个数据结构记录已经计算过的元素。这里通过传递这个集合 \( Aᵢ \) 来实现:
Given an invertible generating function \( F \).
Define the function \( \operatorname{\mathtt{gfp}}^t_F \) (or just \( \operatorname{\mathtt{gfp}}^t \)) as follows:
\begin{aligned} \operatorname{\mathtt{gfp}}^(A, x) = & \operatorname{\mathtt{if}}\ x \in A\ \operatorname{\mathtt{then}}\ A \\ & \operatorname{\mathtt{else\ if}}\ \operatorname{\mathtt{support}}(x) \uparrow\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{fail}} \\ & \operatorname{\mathtt{else}}\ \text{let $\{x_1, \ldots, x_n\} = \operatorname{\mathtt{support}}(x)$ in} \\ & \quad \text{let $A_0 = A \cup \{x\}$ in} \\ & \quad \text{let $A_1 = \operatorname{\mathtt{gfp}}^t(A_0, x_1)$ in} \\ & \quad \dots \\ & \quad \text{let $A_n = \operatorname{\mathtt{gfp}}^t(A_{n-1}, x_n)$ in} \\ & \quad A_n \end{aligned}
To check \( x \in \nu_F \), compute \( \operatorname{\mathtt{gfp}}^t(\emptyset, x) \). If this call succeeds, then \( x \in \nu_F \); if it fails, then \( x \notin \nu_F \).
If an expression \( B \) fails, then “let A = B in C” also fails (similar to exceptions). \).
下面证明这个定义的正确性。
For \( \operatorname{\mathtt{gfp}}^t_F(A, x) \),
If \( \operatorname{\mathtt{gfp}}^t_F(A, x) = A’ \), then \( A \cup \{x\} \subseteq A’ \).
For all \( X \), if \( \operatorname{\mathtt{support}}_F(A) \subseteq A \cup X \cup \{x\} \) and \( \operatorname{\mathtt{gfp}}^t_F(A, x) = A’ \), then \( \operatorname{\mathtt{support}}_F(A’) \subseteq A’ \cup X \).
第一个 lemma 是显然的,对计算过程分类讨论即可。
第二个 lemma 可以通过对计算过程进行归纳得到:
如果 \( x \in A \),那么 \( A’ = A \),成立
否则考虑第三种情况,不妨先考虑 \( \operatorname{\mathtt{support}}(x) = \{x₁, x₂\} \) 的情况,对于更多元素的情况可以类似归纳证明。下面证明 \( \forall X. \operatorname{\mathtt{support}}(A) \subseteq A \cup \{x\} \cup X₀ \implies \operatorname{\mathtt{support}}(A₂) \subseteq A₂ \cup X₀ \)。
考虑
\begin{aligned} \operatorname{\mathtt{support}}(A₀) &{}= \operatorname{\mathtt{support}}(A \cup x) \\ &{}= \operatorname{\mathtt{support}}(A) \cup \operatorname{\mathtt{support}}(x) \\ &{}= \operatorname{\mathtt{support}}(A) \cup \{x₁, x₂\} \\ &{}\subseteq A \cup \{x\} \cup X₀ \cup \{x₁, x₂\} \\ &{}= A₀ \cup X₀ \cup \{x₁, x₂\} \\ &{}= A₀ \cup (X₀ \cup \{x₂\}) \cup \{x₁\} \end{aligned}
根据归纳假设,有 \( \operatorname{\mathtt{support}}(A₁) \subseteq A₁ \cup (X₀ \cup \{x₂\}) \),重复这个步骤可得 \( \operatorname{\mathtt{support}}(A₂) \subseteq A₂ \cup X₀ \)。通过归纳证明可得。
For \( \operatorname{\mathtt{gfp}}^t_F(\emptyset, x) \),
- If \( \operatorname{\mathtt{gfp}}^t_F(\emptyset, x) = A’ \), then \( x \in \nu F \).
- If \( \operatorname{\mathtt{gfp}}^t_F(\emptyset, x) = \operatorname{\mathtt{fail}} \), then \( x \notin \nu F \).
首先考虑第一部分的证明。根据 lemma (1) 有 \( x \in A’ \)。由于 \( \operatorname{\mathtt{support}}(\emptyset) = \emptyset \subseteq \emptyset \cup \emptyset \cup \{x\} \),根据 lemma (2) 有 \( \operatorname{\mathtt{support}}(A’) \subseteq A’ \),根据前面章节证明的 lemma \( \operatorname{\mathtt{support}}(X) \subseteq Y \implies X \subseteq F(Y) \) 有 \( A’ \subseteq F(A’) \),因此 \( x \in A’ \subseteq \nu F \)。
第二部分可以先对 \( \operatorname{\mathtt{gfp}}^t_F \) 的运行过程进行归纳,证明 \( \operatorname{\mathtt{gfp}}^t_F(A, x) = \operatorname{\mathtt{fail}} \implies x \notin \nu F \),然后完成证明。
这些算法的终结性条件则与 \( \operatorname{\mathtt{gfp}} \) 相同。
Subtyping on Infinite Types
前面讨论了 induction 和 coinduction 作为理论基础,下面将利用这些概念来建立 infinite types 上的 subtyping 关系。
Finite and Infinite Types
接下来考虑如何将类型建模为一棵(有穷或无穷的)树。为了方便讨论,这里只考虑三种 type constructor:\( \to, \times, \operatorname{\mathtt{Top}} \)。下面会将类型表示为树,其中树结点会带一个 label \( \to, \times, \operatorname{\mathtt{Top}} \)。
这里用 \( \{ 1, 2 \}^\star \) 表示由 1 和 2 构成的序列的集合,空序列用 \( \cdot \) 表示,\( i^k \) 表示 \( i \) 重复 \( k \) 次,并用 \( \pi, \sigma \) 表示序列 \( \pi \) 和 \( \sigma \) 的连接。
(tree type)
A tree type is a partial function \( T \in \{1, 2\}^\star \rightharpoonup \{\to, ×, \operatorname{\mathtt{Top}}\} \) satisfying the following constraints:
- \( T(•) \) is defined;
- if \( T(\pi, \sigma) \) is defined, then \( T(\pi) \) is defined;
- if \( T(\pi) = \to \) or \( T(\pi) = × \), then \( T(\pi, 1) \) and \( T(\pi, 2) \) are defined;
- if \( T(\pi) = \operatorname{\mathtt{Top}} \), then \( T(\pi, 1) \) and \( T(\pi, 2) \) are undefined.
对这个定义的一个直观理解是它构成了从一个函数到一棵类型二叉树的映射。在序列 \( a₁ a₂ \dots aₙ\ (a₁, a₂ \in \{ 1, 2 \}) \) 中,\( 1 \) 表示向左走,\( 2 \) 表示向右走,\( T(a₁ a₂ \dots aₙ) \) 表示在树中走到这个结点时的 label;而 \( T(\cdot)\) 则表示根结点的符号。
容易看出Tree \(T\) 是有穷的当且仅当 \( \operatorname{\mathtt{dom}}(T) \) 是有穷的。所有 trees 构成的集合记作 \( \mathcal{T} \),其中有穷 tree 构成的集合记作 \( \mathcal{T}_f \)。
为了方便讨论:
- 当树满足 \( T(\cdot) = \operatorname{\mathtt{Top}} \) 时将其记作 \( \operatorname{\mathtt{Top}} \)
- 当树表示 \( T(\cdot) = \times \) 且 \( T(\cdot)(i, \pi) = Tᵢ(\pi) \) 时将其记作 \( T₁ \times T₂ \)
- 当树表示 \( T(\cdot) = \to \) 且 \( T(\cdot)(i, \pi) = Tᵢ(\pi) \) 时将其记作 \( T₁ \to T₂ \)
下面时两个例子:
有穷类型 \( (\operatorname{\mathtt{Top}} \times \operatorname{\mathtt{Top}}) \to \operatorname{\mathtt{Top}}\) 表示左边的树,它满足
\[ T(\cdot) = \to \] \[ T(1) = \times \] \[ T(2) = T(1, 1) = T(1, 2) = \operatorname{\mathtt{Top}} \]
无穷类型 \( \operatorname{\mathtt{Top}} \to (\operatorname{\mathtt{Top}} \to \dots) \) 表示右边的树,它满足
\[ T(\cdot) = \to \] \[ T(2^k) = \to \] \[ T(2^k, 1) = \operatorname{\mathtt{Top}} \]
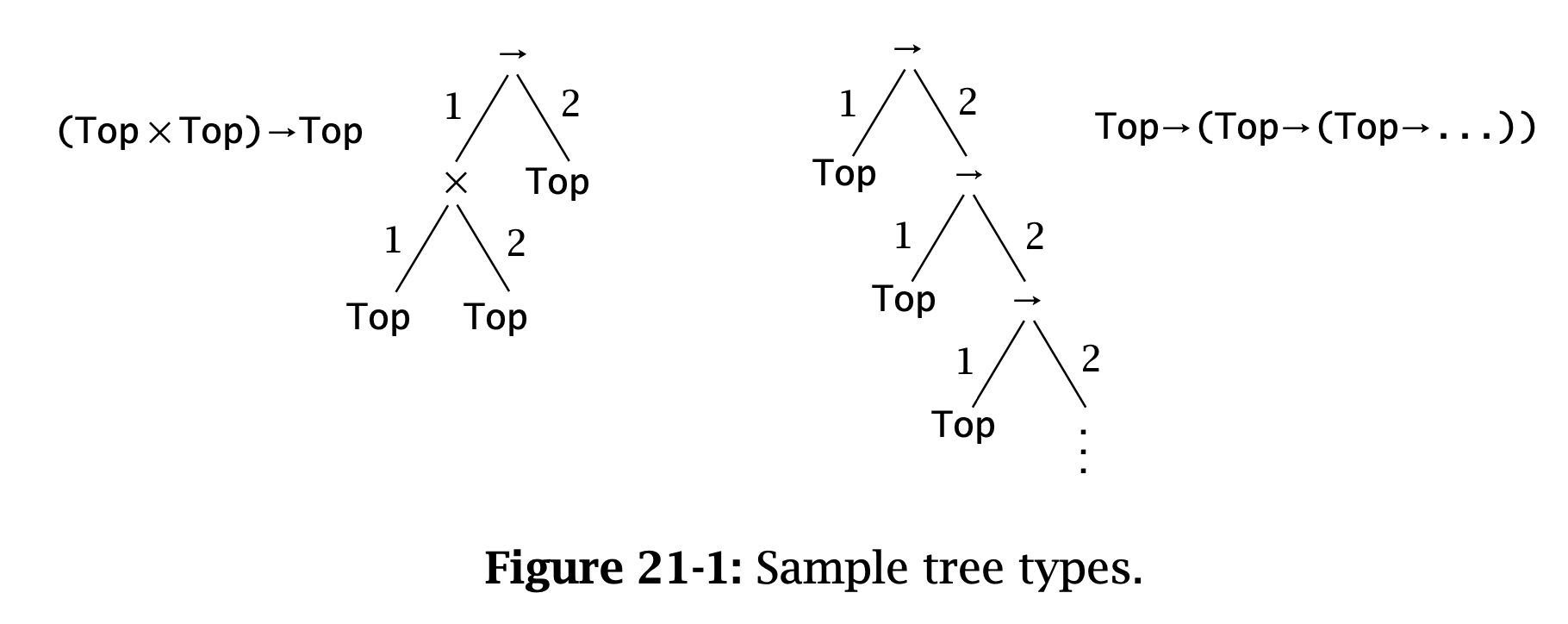
Figure 2: 21-1-sample-tree-types
这样的 tree 可以被形式化为 BNF 语法:\( T \Coloneqq \operatorname{\mathtt{Top}} | T \times T | T \to T \)。
Exists a universe \( \mathcal{U} \) and a generating function \( F \in \mathcal{P}(\mathcal{U}) \to \mathcal{{P}}(\mathcal{U}) \) such that \( \mathcal{T}_f = \mu F \) and \( \mathcal{T} = \nu F \).
定义一个树为一个部分函数 \( T \in \{1, 2\}^\star \rightharpoonup \{\to, ×, \operatorname{\mathtt{Top}}\} \),满足以下约束条件:
- \( T(•) \) 已定义;
- 如果 \( T(\pi, \sigma) \) 已定义,则 \( T(\pi) \) 已定义。
- 注意,这里对树节点中的符号没有约束,例如,标记为 \( \operatorname{\mathtt{Top}} \) 的节点也可以有子节点。
将所有树的集合作为 \( \mathcal{U} \),因此 \( \mathcal{T} \subseteq \mathcal{U} \)。\( \mathcal{U} \) 上的 \( F \) 的定义类似 BNF:
\begin{aligned} F(X) &= \{ \operatorname{\mathtt{Top}} \} \\ &\cup \{ T₁ \times T₂ \mid T₁, T₂ \in X \} \\ &\cup \{ T₁ \to T₂ \mid T₁, T₂ \in X \}. \end{aligned}
为了证明 \( \mathcal{T} = \nu F \),需要证明 \( \mathcal{T} \subseteq \nu F \) 和 \( \nu F \subseteq \mathcal{T} \):
- 显然 \( \mathcal{T} \in F(\mathcal{T}) \),因此 \( \mathcal{T} \) 是 \( F \)-consistent 的。所以 \( \mathcal{T} \subseteq \nu F \)
- 要证明 \( \nu F \subseteq \mathcal{T} \),只要证明 \( T \in \nu F \implies T \in \mathcal{T} \),即 \( T \) 满足 \( \mathcal{T} \) 的后两个条件。
- 根据定义由 \( T \in \nu F \) 知 \(T \in F(\nu F)\)。根据 \( F \) 的定义知对于 \( T(\pi) \),当 \( |\pi| = 0 \) 时有 \( T(\cdot) = \operatorname{\mathtt{Top}} \),当 \( |\pi| > 0 \) 时有 \( T(\pi) = T₁ \to T₂ \) 或 \( T(\pi) = T₁ \times T₂ \)
- 任取 \( T \in \nu F, \pi \in \{1, 2\}^{\star} \),考虑 \( T(\pi) \),对 \( \pi \) 的长度进行归纳:
- 当 \( |\pi| = 0 \) 即 \( \pi = \cdot \) 时,必定有 \( T(\cdot) = \operatorname{\mathtt{Top}} \),满足最后一个条件。
- 设当 \( |\pi| < n \) 时,若 \( T \in \nu F \),则 \( T(\pi) \) 满足条件。当 \( |\pi| = n \) 时,必定有 \( T(\pi) = T₁ \to T₂ \) 或 \( T(\pi) = T₁ \times T₂ \),满足倒数第二个条件。
- 因此 \( T \in \nu F \implies T \in \mathcal{T} \)
然后要证明 \( \mathcal{T}_f = \mu F \),即证明 \( \mu F \subseteq \mathcal{T}_f \) 和 \( \mathcal{T}_f \subseteq \mu F \):
- 显然 \( F(\mathcal{T}_f) \subseteq \mathcal{T}_f \),因此 \( \mathcal{T}_f \) 是 \( F \)-closed 的。所以 \( \mu F \subseteq \mathcal{T}_f \)
- 然后要证明 \( T \in \mathcal{T}_f \implies T \in \mu F \),对 \( T \) 的长度(作用域中最长序列 \( \pi \in \{1, 2\}^\star \) 的长度)进行归纳:
- 当 \(|T| = 0\) 时,只存在 \( T(\cdot) = \operatorname{\mathtt{Top}} \) 使得 \( T \in \mathcal{T}_f \)。下面证明 \( T \in \mu F \):
- 设集合 \( X \) 是 \( F \)-closed 的,即 \( F(X) \subseteq X \),又 \( \forall X. \operatorname{\mathtt{Top}} \in F(X) \),因此有 \( F(X) \subseteq X \implies \operatorname{\mathtt{Top}} \in X \),因此 \( \operatorname{\mathtt{Top}} \in \mu F \)。
- 设当 \(|T| < n\) 时,对任意 \( T \in \mathcal{T}_f \) 有 \( T \in \mu F \)。当 \(\operatorname{\mathtt{size}}(T) = n\) 时,一定有 \( T = T₁ \to T₂ \) 或 \( T = T₁ \times T₂ \)。设 \( T₁, T₂ \in \mathcal{T}_f \) 且 \( |T₁| < n \land |T₂| < n \),根据递归假设有 \( T₁, T₂ \in \mu F \),因此 \( T₁ \to T₂ \in \mu F \wedge T₁ \times T₂ \in \mu F\)。
- 因此 \( T \in \mathcal{T}_f \implies T \in \mu F \)
- 当 \(|T| = 0\) 时,只存在 \( T(\cdot) = \operatorname{\mathtt{Top}} \) 使得 \( T \in \mathcal{T}_f \)。下面证明 \( T \in \mu F \):
这个证明的两边结论不一样的关键在于 \( T \in \nu F \implies T \in \mathcal{T} \) 这句话:\( T \in \nu F \implies T \in \mathcal{T}_f \) 不成立,因为 \( T \) 可能是一个无穷类型。容易推论出如果 \( U \) 中只包含有穷类型,那么有 \( \mu F = \nu F \)。
Subtyping
下面将 subtyping 关系定义为特定宇宙中单调函数的最小 fixed-point 和最大 fixed-point。对于有穷树类型上的 subtyping, \( \mathcal{U} = \mathcal{T}_f \times \mathcal{T}_f \),\( F: \mathcal{T}_f \times \mathcal{T}_f \to \mathcal{T}_f \times \mathcal{T}_f \);对于任意类型树(有穷类型树或者无穷类型树)上的 subtyping, \( \mathcal{U} = \mathcal{T} \times \mathcal{T} \),\( F: \mathcal{T} \times \mathcal{T} \to \mathcal{T} \times \mathcal{T} \)。
(Finite subtyping)
Two finite tree types \( S \) and \( T \) are in the subtype relation if \( (S, T) ∈ \mu S_f \) , where the monotone function \( S_f \in \mathcal{P}(\mathcal{T}_f \times \mathcal{T}_f) \to \mathcal{P}(\mathcal{T}_f \times \mathcal{T}_f) \) is defined by
\begin{aligned} S_f( R) &= \{ (T, \operatorname{\mathtt{Top}}) \mid T \in \mathcal{T}_f \} \\ &\cup \{ (S_1 \times S_2, T_1 \times T_2) \mid (S_1, T_1), (S_2, T_2) \in R \} \\ &\cup \{ (S_1 \to S_2, T_1 \to T_2) \mid (T_1, S_1), (S_2, T_2) \in R \}. \end{aligned}
这个定义对应了三条 subtyping 规则(此处 inference rules 的含义为如果横线上方的部分在是参数,则横线下面的部分是结果):
\[ \frac{}{\operatorname{\mathtt{Top}} <: S} \]
\[ \frac{S₁ <: T₁ \quad S₂ <: T₂}{S₁ \times S₂ <: T₁ \times T₂} \]
\[ \frac{T₁ <: S₁ \quad S₂ <: T₂}{S₁ \to S₂ <: T₁ \to T₂} \]
(Infinite subtyping)
Two (finite or infinite) tree types \( S \) and \( T \) are in the subtype relation if \( (S, T) ∈ \nu S \) , where the monotone function \( S \in \mathcal{P}(\mathcal{T} \times \mathcal{T}) \to \mathcal{P}(\mathcal{T} \times \mathcal{T}) \) is defined by
\begin{aligned} S( R) &= \{ (T, \operatorname{\mathtt{Top}}) \mid T \in \mathcal{T} \} \\ &\cup \{ (S₁ \times S₂, T₁ \times T₂) \mid (S₁, T₁), (S₂, T₂) \in R \} \\ &\cup \{ (S₁ \to S₂, T₁ \to T₂) \mid (T₁, S₁), (S₂, T₂) \in R \}. \end{aligned}
这个定义和有穷 subtyping 的定义类似,但是它考虑了一个更大的宇宙,并使用了 greatest fixed-point。
是否存在一对类型 \( (S, T) \in \nu S \),但 \( (S, T) \notin \mu S \)。
假设 \( T \) 是无穷类型,下面证明 \( (T, T) \) 满足条件。考虑 \( R = \{ Q \mid \text{$Q$ is a subtree of $T$} \} \),容易证明 \( R \subseteq S( R) \),因此 \( R \subseteq \nu S \),即 \( (T, T) \in \nu S \)。
注意这里 \( \mu S \) 包含无穷类型(来自 \( (T, \operatorname{\mathtt{Top}}) \))。下面用反证法证明 \( (T, T) \notin \mu S \)。
假设 \( (T, T) \in \mu S \)。由于 \( \mu F = \bigcup \{F^{n}(\emptyset) \mid n \ge 0\} \),因此必定存在一个最小的 \( n \ge 0 \) 使得 \( (T, T) \in F^{n}(\emptyset) \)。由于 \( T \) 是无穷类型,因此必有 \( T = T₁ \times T₂ \) 或 \( T = T₁ \to T₂ \),其中 \( T₁\) 或 \( T₂ \) 是无穷类型且 \( (T₁, T₁) \in F^{n-1}(\emptyset) \lor (T₂, T₂) \in F^{n-1}(\emptyset) \)。依次类推,可知存在无穷类型 \( T’ \) 使得 \( (T’, T’) \in F(\emptyset) \) 。而 \( F(\emptyset) = \{(\operatorname{\mathtt{Top}}, \operatorname{\mathtt{Top}})\} \cup \{(T, \operatorname{\mathtt{Top}}) \mid T \ne \operatorname{\mathtt{Top}}\} \),矛盾,因此 \( (T, T) \notin \mu S \)。
因此 \( (T, T) \in \nu S \land (T, T) \notin \mu S \)。
是否存在一对类型 \( (S, T) \in \nu S_f \),但 \( (S, T) \notin \mu S_f \)。
不存在,因为在 \( S_f \) 中 \( \mu S_f = \nu S_f \)(对 \( S, T \) 的 size 进行归纳即可)。
Transitivity and Reflexivity
下面证明在无穷类型上 subtyping 关系的自反性和传递性。
\( S \) is reflexive.
首先定义树类型上的恒等关系:\(I = \{(T, T) | T ∈ T\}\)。然后只要证明 \(I \subseteq νS\),即证明 \(I\) 的 \(S\)-consistent 的,即证明 \( I \subseteq S(I) \)。
取 \((T, T) \in I\),并对 \(T\) 进行归纳:
- \(T = \operatorname{\mathtt{Top}}\),则 \((T, T) = (\operatorname{\mathtt{Top}}, \operatorname{\mathtt{Top}}) \in S(I)\)
- \(T = T₁ × T₂ \)。由于 \((T_1, T_1) \in I \wedge (T_2, T_2) \in I\),根据 \(S\) 的定义,可以推得 \((T1 × T2, T1 × T2)\) 属于 \(S(I)\)。
- \( T = T₁ \to T₂ \) 同理。
接下来讨论传递性。首先定义一个函数 \( \operatorname{\mathtt{TR}} \in \mathcal{P}(\mathcal{U} \times \mathcal{U}) \to \mathcal{P}(\mathcal{U} \times \mathcal{U}) \):
\[ \operatorname{\mathtt{TR}}( R) = \{ (S, T) \mid \exists U. (S, U) \in R \land (U, T) \in R \} \]
容易看出如果 \( \operatorname{\mathtt{TR}}( R) \subseteq R \) 则 \( R \) 是传递的。
Let \( F \in \mathcal{P}(\mathcal{U} \times \mathcal{U}) \to \mathcal{P}(\mathcal{U} \times \mathcal{U}) \) be a monotone function. If \( \operatorname{\mathtt{TR}}(F( R)) \subseteq F(\operatorname{\mathtt{TR}}( R)) \) for any \( R \subseteq \mathcal{U} \times \mathcal{U} \), then \( \nu F \) is transitive.
易知
\[\nu F = F(\nu F) \implies \operatorname{\mathtt{TR}}(\nu F) = \operatorname{\mathtt{TR}}(F(\nu F)) \subseteq F(TR(\nu F))\]
因此 \( \operatorname{\mathtt{TR}}(\nu F) \) 是 \( F \)-consistent 的,因此 \( \operatorname{\mathtt{TR}}(\nu F) \subseteq \nu F \),即 \( \nu F \) 是传递的。
这个 lemma 的条件部分 \( \operatorname{\mathtt{TR}}(F( R)) \subseteq F(\operatorname{\mathtt{TR}}( R)) \) 有点像 cut-elimination(在 subtyping 中消去传递规则时证明)。如果把 \( R \) 看作 statements 的集合,并且将其先应用于 \( F \) 然后用传递规则,那么这个条件意味着可以先将其应用传递规则,再用于 \( F \)。
\( \nu S \) is transitive.
要证明 \( \nu S \) 是传递的,根据上面的 lemma 知只要证明 \(\forall R \in (\mathcal{T}, \mathcal{T}). \operatorname{\mathtt{TR}}(S( R)) \subseteq S(\operatorname{\mathtt{TR}}( R)) \):
取 \( (S, T) \in \operatorname{\mathtt{TR}}(S( R)) \),则存在 \( U \) 使得 \( (S, U) \in S( R) \land (U, T) \in S( R) \)。下面证明 \( (S, T) \in S(\operatorname{\mathtt{TR}}( R)) \),对 \( U \) 进行归纳:
\( U = \operatorname{\mathtt{Top}} \),则 \( T = \operatorname{\mathtt{Top}} \),因此 \( (S, T) = (S, \operatorname{\mathtt{Top}}) \)。由于 \(\forall R’. \operatorname{\mathtt{Top}} \in S(R’) \),因此 \( (S, \operatorname{\mathtt{Top}}) \in S(\operatorname{\mathtt{TR}}( R)) \) 成立
\( U = U₁ \to U₂ \)
- 假设 \( T = \operatorname{\mathtt{Top}} \),那么同上一种情况,显然成立
- \( T = T₁ \to T₂ \) 并且 \( S = S₁ \to S₂ \)。根据归纳假设有 \( (S₁, U₁) \in S( R) \land (U₁, T₁) \in S( R) \) 且 \( (S₂, U₂) \in S( R) \land (U₂, T₂) \in S( R) \),因此 \( (S₁ \to S₂, T₁ \to T₂) \in S(\operatorname{\mathtt{TR}}( R)) \) 成立
\( U = U₁ \times U₂ \) 同理
Degression: Transitivity in coinduction
在类型系统设计中,declarative presentations 和 algorithmic presentations 是两种不同的形式化方式。前者强调可读性,并且包含传递规则(transitivity rule)。在 declarative presentations 中明确传递规则有两个优势:首先,它明确展示了 subtyping 的传递性;其次,它简化了其他几条规则的表述,使它们更直观和基础。然而,这条规则在实际的算法中并不适用,因为传递规则 \( S <: U \wedge U <: T \implies S <: U \) 会要求算法猜测中间类型 \( U \),这在算法执行时不可行。
有趣的是,能够在 declarative subtyping presentations 中分离出传递规则是 inductive definition 的性质。Transitivity 是一个闭包属性:意味着这组规则将在传递规则下封闭。在 subtyping rules 中添加传递规则后,所得并集的闭包(即 declarative subtyping presentations)自动具备了 transivitiy。这实际上是 inductive definition 的一个性质:两组规则的并集被 inductively-applied 时,生成的关系是最小的能够两组规则下同时分别封闭的关系。
Suppose \(F, G\) are monotone functions, and let \(H(X) = F(X) \cup G(X)\). Then \(\mu H\) is the smallest set that is both \(F\)-closed and \(G\)-closed.
由于有 \(\mu H = H(\mu H) = F(\mu H) \cup G(\mu H)\),因此 \(F(\mu H) \subseteq \mu H\) 且 \(G(\mu H) \subseteq \mu H\),即 \(\mu H\) 满足 \(F\)-closed 且 \(G\)-closed。
设存在集合 \(X\) 满足 \(F(X) \subseteq X \wedge G(X) \subseteq X\)。那么 \(H(X) = F(X) \cup G(X) \subseteq X\),即 \(X\) 是 \(H\)-closed 的。根据 Knaster-Tarski 定理,\(\mu H\) 是最小的 \(H\)-closed 集合,因此有 \(\mu H \subseteq X\),即 \(\mu H\) 是同时满足 \(F\)-closed 和 \(G\)-closed 的最小集合。
然而对于 coinductive definitions,这个性质并不成立。下面的定理说明这样做会导致得到一个退化的关系(最大的同时对两组规则封闭的关系)。
Suppose \(F\) is a generating function on the universe \(\mathcal{U}\). Show that the greatest fixed point \( \nu F_{TR} \) of the generating function
\[F_{\operatorname{\mathtt{TR}}}( R) = F( R) \cup \operatorname{\mathtt{TR}}( R)\]
is the total relation on \(\mathcal{U} \times \mathcal{U}\) (i.e. \( \nu F_{TR} = \mathcal{U} \times \mathcal{U}\)).
设 \( (x, y) \in \mathcal{U} \times \mathcal{U} \),任取 \( z \in \mathcal{U} \) 则有 \( (x, z), (z, y) \in \mathcal{U} \times \mathcal{U} \),因此 \( (x, y) \in \operatorname{\mathtt{TR}}(\mathcal{U} \times \mathcal{U}) \subseteq F^{\operatorname{\mathtt{TR}}}(\mathcal{U} \times \mathcal{U})\)。因此 \( \mathcal{U} \times \mathcal{U} \subseteq F^{\operatorname{\mathtt{TR}}}(\mathcal{U} \times \mathcal{U}) \),即 \( \mathcal{U} \times \mathcal{U} \) 是 \( F^{\operatorname{\mathtt{TR}}} \)-consistent 的。则 \( \mathcal{U} \times \mathcal{U} = \nu F^{\operatorname{\mathtt{TR}}}\),得证。
因此,在 coinductive definitions 中,只考虑 algorithmic presentations,如果考虑 declarative presentations 并分离出传递规则,其生成的闭包会退化为整个宇宙。
μ-Types
Regular Trees
目前已经利用 induction 和 coinduction 定义了 infinite types 上的 subtyping 关系,并且讨论了 induction 和 coinduction definitions 中的 member checking 算法。下面将合并这两部分的结果,证明如果只考虑一类特殊的 regular tree types,那么能保证这样的集合满足 finite-state,进而保证在 subtyping 关系上的 membership checking 的停机性。
(Subtrees)
A tree type \( S \) is a subtree of a tree type \( T \) if \( S = \lambda \sigma. T(\pi, \sigma) \) for some \( \pi \) — that is, if the function \( S \) from paths to symbols can be obtained from the function \( T \) by adding some constant prefix \( \pi \) to the argument paths we give to \( T \). The prefix \( \pi \) corresponds to the path from the root of \( T \) to the root of \( S \).
We write \( \operatorname{\mathtt{subtrees}}(T) \) for the set of all subtrees of \( T \).
(Regular Trees)
A tree type \( T \in \mathcal{T} \) is regular if \( \operatorname{\mathtt{subtrees}}(T) \) is finite — i.e., if \( T \) has finitely many distinct subtrees.
The set of regular tree types is denoted by \( \mathcal{T}_r \).
显然一个“表述上有穷”的无穷 recursive type 都是 regular 的,例如 \( T = \operatorname{\mathtt{Top}} \times T \)。
下面是一个非 regular 的例子:
\[T = B \times (A \times (B \times (A \times (A \times (B \times (A \times (A \times (A \times (B \times \dots))))))\]
The restriction \( S_r \) of the generating function \( S \) to regular tree types is finite state.
只需要证明,\( \forall(S, T) \in \mathcal{T}ᵣ \times \mathcal{T}ᵣ. \operatorname{\mathtt{reachable}}_{S_r}(S, T) \) 是有穷的。
不难发现 \( \operatorname{\mathtt{reachable}}_{S_r}(S, T) \subseteq \operatorname{\mathtt{subtrees}}(S) \times \operatorname{\mathtt{subtrees}}(T) \cup \operatorname{\mathtt{subtrees}}(T) \times \operatorname{\mathtt{S}} \);由于 \( \operatorname{\mathtt{subtrees}}(S) \) 和 \( \operatorname{\mathtt{subtrees}}(T) \) 都是有限的,所以后者也是有限的。
由此可以发现,对于 regular tree types,可以利用 membership checking 的算法来判断 subtyping 关系。
μ-Types
本节将通过 μ-notation 来“有穷地”表述 regular tree types,定义 μ-expressions 上的 subtyping 关系,并建立 μ-types 和 tree types 之间的关系。
(μ-types)
Let \( X \) range over a fixed countable set \(\{X_1, X_2, \dots\}\) of type variables. The set \(\mathcal{T}^{\operatorname{\mathrm{raw}}}ₘ\) of raw μ-types is the set of expressions defined by the following grammar:
\begin{aligned} \mathcal{T} \Coloneqq &{} X \\ &{} \operatorname{\mathtt{Top}} \\ &{} T \times T \\ &{} T \to T \\ &{} \mu X. T \end{aligned}
The syntactic operator \( \mu \) is a binder, and gives rise to notions of bound and free variables, closed raw μ-types, and equivalence of raw μ-types up to renaming of bound variables.
\( \operatorname{\mathtt{FV}}(T) \) denotes the set of free variables of a raw μ-type \( T \).
The capture-avoiding substitution \( [X \mapsto S]T \) of a raw μ-type \( S \) for free occurrences of \( X \) in a raw μ-type \( T \) is defined as usual.
μ-types 定义了类型上的 \( \operatorname{\mathtt{fix}} \)。其中 \( \mu \) 和 \( \lambda \) 类似,能够引入类型变量,但是它的操作不是 application,而是类似 \( \operatorname{\mathtt{fix}} \) 的 unfolding:
\[\mu X. T \xRightarrow{\operatorname{\mathrm{unfolding}}} [X \mapsto \mu X. T] T\]
下面需要将 μ-types 的展开和无穷 tree types 建立联系。需要注意的是有一类特殊的 μ-types 无法展开,其形式为 \( \mu X. \mu X₁ \dots \mu Xₙ. X \),例如 \( T = \mu X. X \),它展开后仍然是 \( T \),在这些类型可能会导致无穷展开。
(contractiveness)
A raw μ-type \( T \) is contractive if, for any subexpression of \( T \) of the form \( \mu X. \mu X_1 \dots \mu X_n. S \), the body \( S \) is not \( X \). (Equivalently, a raw μ-type is contractive if every occurrence of a μ-bound variable in the body is separated from its binder by at least one \( \to \) or \( \times \).)
A raw μ-type is called simply a μ-type if it is contractive. The set of μ-types is written \( \mathcal{T}_m \).
When \( T \) is a μ-type, we write \( \mu-\operatorname{\mathtt{height}}(T) \) for the number of μ-bindings at the front of \( T \).
在 contractiveness 保证下,每次 unfolding 后,一定会先遇到 \( \times \) 或 \( \to \),这使得下面的 \( \operatorname{\mathtt{treeof}} \) 能够停机。
(\( \operatorname{\mathtt{treeof}} \))
The function \( \operatorname{\mathtt{treeof}} \), mapping closed μ-types to tree types, is defined inductively as follows:
\begin{aligned} &\operatorname{\mathtt{treeof}}(\operatorname{\mathtt{Top}})(\cdot) &&= \operatorname{\mathtt{Top}} \\ \\ &\operatorname{\mathtt{treeof}}(T₁ \to T₂)(\cdot) &&= \to \\ &\operatorname{\mathtt{treeof}}(T₁ \to T₂)(i, \pi) &&= \operatorname{\mathtt{treeof}}(Tᵢ)(\pi) \\ \\ &\operatorname{\mathtt{treeof}}(T₁ \times T₂)(\cdot) &&= \times \\ &\operatorname{\mathtt{treeof}}(T₁ \times T₂)(i, \pi) &&= \operatorname{\mathtt{treeof}}(Tᵢ)(\pi) \\ \\ &\operatorname{\mathtt{treeof}}(\mu X. T)(\pi) &&= \operatorname{\mathtt{treeof}}([X \mapsto \mu X. T]T)(\pi) \\ \end{aligned}
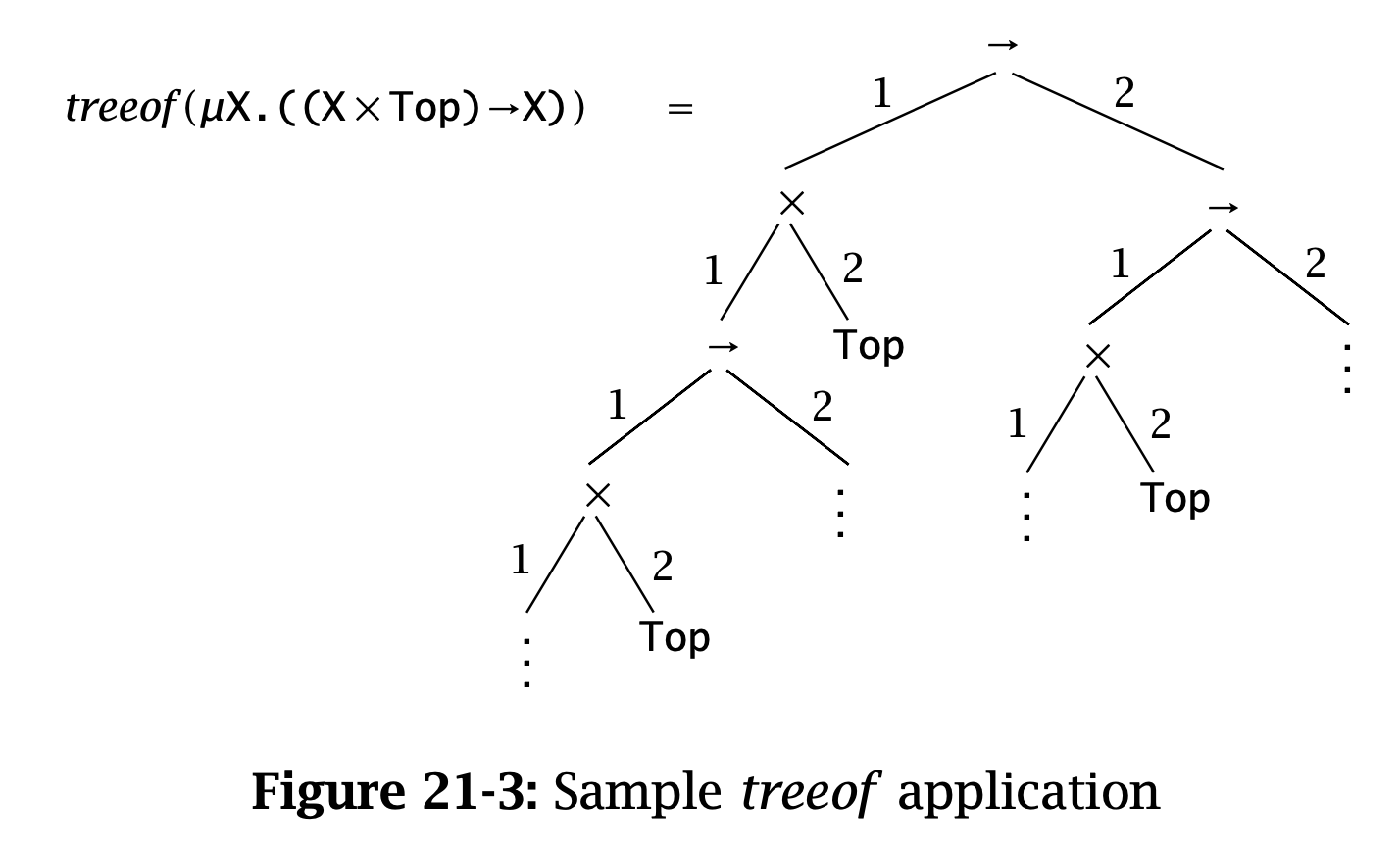
Figure 3: 21-3-sample-treeof-application
注意这是一个二元的递归函数,下面讨论它的停机性:
- 每次对 \( \operatorname{\mathtt{treeof}} \) 的递归调用中,考虑 \( (| \pi |, \mu-\operatorname{\mathtt{height}}(T)) \),每次要么会减小 \( | \pi | \),要么会减小 \( \mu-\operatorname{\mathtt{height}}(T) \),因此 \( \times \) 和 \( \to \) 的递归会终止
- 每次递归调用都保持了 contractiveness 和 closure,即 \( \mu X. T \) contractive 且 closed 仅当 \( [X \mapsto \mu X. T] T \) 也是 contractive 且 closed,因此不会无穷展开
为了方便起见,将 \( \operatorname{\mathtt{treeof}} \) 扩展到 types pairs:\( \operatorname{\mathtt{treeof}}(S, T) = (\operatorname{\mathtt{treeof}}(S), \operatorname{\mathtt{treeof}}(T)) \)。
Subtyping on μ-types
下面定义 μ-types 上的 subtyping 关系,与 tree types 上的 subtyping 关系类似,但是需要考虑 μ-types 的 unfolding,由下面两套规则描述:
\[ \frac{S <: [X \mapsto \mu X.T]T}{S <: \mu X.T} \]
\[ \frac{[X \mapsto \mu X.S]S <: T}{\mu X.S <: T} \]
Two μ-types \( S \) and \( T \) are said to be in the subtype relation if \( (S, T) \in \nu S_m \), where the monotone function \( S_m \in \mathcal{P}(\mathcal{T}_m \times \mathcal{T}_m) \to \mathcal{P}(\mathcal{T}_m × \mathcal{T}_m) \) is defined by:
\begin{aligned} S_m( R) = & \{(S, \operatorname{\mathtt{Top}}) \mid S \in \mathcal{T}_m\} \\ & \cup \{(S_1 \times S_2, T_1 \times T_2) \mid (S_1, T_1), (S_2, T_2) \in R\} \\ & \cup \{(S_1 \rightarrow S_2, T_1 \rightarrow T_2) \mid (T_1, S_1), (S_2, T_2) \in R\} \\ & \cup \{(S, \mu X.T) \mid (S, [X \mapsto \mu X.T]T) \in R\} \\ & \cup \{(\mu X.S, T) \mid ([X \mapsto \mu X.S]S, T) \in R, T \neq \operatorname{\mathtt{Top}} \land T \neq \mu Y.T_1\}. \end{aligned}
这里在最后一条规则上增加了额外限制条件以避免规则之间重叠,二者实际上得到的集合闭包是一样的,但是这个限制能保证 \( Sₘ \) 是 invertible 的:
\[\operatorname{\mathtt{support}}_{S_m}(S, T) = \begin{cases} \emptyset & \text{if $T = \operatorname{\mathtt{Top}}$} \\ \{(S_1, T_1), (S_2, T_2)\} & \text{if $S = S_1 \times S_2$ and $T = T_1 \times T_2$} \\ \{(T_1, S_1), (S_2, T_2)\} & \text{if $S = S_1 \to S_2$ and $T = T_1 \to T_2$} \\ \{(S, [X \mapsto \mu X . T_1] T_1)\} & \text{if $T = \mu X . T_1$} \\ \{([X \mapsto \mu X . S_1] S_1, T)\} & \text{if $S = \mu X . S_1$ and $T \neq \mu X . T_1$ and $T \neq \operatorname{\mathtt{Top}}$} \\ \uparrow & \text{otherwise} \end{cases}\]
定义
\begin{aligned} S_d( R) = & \{(S, \operatorname{\mathtt{Top}}) \mid S \in \mathcal{T}_m\} \\ & \cup \{(S_1 \times S_2, T_1 \times T_2) \mid (S_1, T_1), (S_2, T_2) \in R\} \\ & \cup \{(S_1 \rightarrow S_2, T_1 \rightarrow T_2) \mid (T_1, S_1), (S_2, T_2) \in R\} \\ & \cup \{(S, \mu X.T) \mid (S, [X \mapsto \mu X.T]T) \in R\} \\ & \cup \{(\mu X.S, T) \mid ([X \mapsto \mu X.S]S, T) \in R\}. \end{aligned}
证明\( S_d \) 不是 invertible 的,且 \( \nu S_d = \nu S_m \)。
考虑 \( G_{(\mu X. \operatorname{\mathtt{Top}}, \mu Y. \operatorname{\mathtt{Top}})} = \{\{(\operatorname{\mathtt{Top}}, \mu Y. \operatorname{\mathtt{Top}})\}, \{(\mu X. \operatorname{\mathtt{Top}}, \operatorname{\mathtt{Top}})\}\}\),因此 \( S_d \) 不是 invertible 的。
由于 \( S_d \) 的限制条件更宽松,因此显然有 \( \nu Sₘ \subseteq \nu S_d \)。所以只需要证明 \( \nu S_d \subseteq \nu Sₘ \)。下面证明 \( \forall (S, T) \in \nu S_d. (S, T) \in \nu Sₘ\)。
注意到 \( S_d \) 和 \( Sₘ \) 的差别仅在于最后一条规则的限制,实际上只要重新安排规则应用的顺序即可:构造时必须先使用 \(\frac{[X \mapsto \mu X.S]S <: T}{\mu X.S <: T}\) 然后再使用 \(\frac{S <: [X \mapsto \mu X.T]T}{S <: \mu X.T}\)(反过来,即在判定时必须先展开右侧,再展开左侧)。
考虑对 \( k = \mu-\operatorname{\mathtt{height}}(S) \) 进行归纳:
- 当 \( k = 0 \) 时:
- 如果 \( T = \mu X₀. \dots \mu Xₙ. T’ \text{ where } T’ \ne \mu Y. T₁ \),那么应用 \( n \) 次 \( \frac{S <: [X \mapsto \mu X.T]T}{S <: \mu X.T} \)
- 否则应用前面的几条规则即可
- 设当 \( k = n \) 时,设 \( \forall (S, T) \in \nu S_d. (S, T) \in \nu Sₘ \)。则当 \( S = \mu X. \mu X₀. \dots \mu Xₙ. S’ \text{ where } S’ \ne \mu Y. S₁\) 时:
如果 \( T = \mu X₀. \dots \mu Xₘ. T’ \text{ where } T’ \ne \mu Y. T₁ \)。根据归纳假设有 \( (\mu X₀. \dots \mu Xₙ. S’, \mu X₀. \dots \mu Xₘ. T’) \in \nu Sₘ \),因此存在一个构造顺序:
\begin{aligned} & (S’, T’) \in \nu Sₘ \\ \Rightarrow & (\mu Xₙ. S’, T’) \in \nu Sₘ \\ \Rightarrow & \dots \\ \Rightarrow & (\mu X₀. \dots \mu Xₙ. S’, T’) \in \nu Sₘ \\ \Rightarrow & (\mu X₀. \dots \mu Xₙ. S’, \mu Xₘ. T’) \in \nu Sₘ \\ \Rightarrow & \dots \\ \Rightarrow & (\mu X₀. \dots \mu Xₙ. S’, \mu X₀. \dots \mu Xₘ. T’) \in \nu Sₘ \end{aligned}
只要在第 \( n \) 步时插入一步 \(\frac{[X \mapsto \mu X.S]S <: T}{\mu X.S <: T}\) 即可。
否则同理
- 综上所述,命题得证。
Equivalence of μ-types and Regular Trees
Suppose that \( R \subseteq \mathcal{T}_m \times \mathcal{T}_m \) is \( Sₘ \)-consistent.
\[ \forall (S,T) \in R.\ \exists (S’, T’) \in R.\ \operatorname{\mathtt{treeof}}(S’, T’) = \operatorname{\mathtt{treeof}}(S, T) \]
where \( \mu-\operatorname{\mathtt{height}}(S’) = \mu-\operatorname{\mathtt{height}}(T’) = 0 \)。
对 \( \mu-\operatorname{\mathtt{height}}(S) + \mu-\operatorname{\mathtt{height}}(T) \) 进行归纳:
- 如果 \( \mu-\operatorname{\mathtt{height}}(S) = \mu-\operatorname{\mathtt{height}}(T) = 0 \),则取 \( S’ = S, T’ = T \) 即可
- 如果 \( (S, T) = (S, \mu X. T₁) \)。由于 \( R \) 是 \( Sₘ \)-consistent 的,有 \( (S, T) \in Sₘ( R) \),根据规则代入有 \( (S, [X \mapsto \mu X. T₁]T₁) \in R\)。由于 \( T \) 是 contractive 的,因此 \( \mu-\operatorname{\mathtt{height}}(T’’) = \mu-\operatorname{\mathtt{height}}([X \mapsto \mu X. T₁]T₁) \) 减少了。根据归纳假设, \(\exists (S’, T’) \in R. \operatorname{\mathtt{treeof}}(S, T’’) = (S’, T’) \),因此 \( \operatorname{\mathtt{treeof}}(S, T) = \operatorname{\mathtt{treeof}}(S, T’’) = (S, T’) \)
- 如果 \( (S, T) = (\mu X. S₁, T) \),同理
这个 lemma 说明 μ-types 可以展开所有顶部的 \( \mu \) 以得到等价的 μ-type。
Let \( (S, T) \in \mathcal{T}ₘ \times \mathcal{T}ₘ \), then
\[(S, T) \in \nu Sₘ \iff \operatorname{\mathtt{treeof}}(S, T) \in \nu S\]
首先证明充分性,即 \( (S, T) \in \nu S_m \implies \operatorname{\mathtt{treeof}}(S, T) \in \nu S \)。设 \( (A, B) = \operatorname{\mathtt{treeof}}(S, T) \in \operatorname{\mathtt{treeof}}(\nu Sₘ) \),只要证明 \( Q = \operatorname{\mathtt{treeof}}(\nu Sₘ) \) 是一个 \( S \)-consistent 的集合即可,即证明 \( \forall (A’, B’) \in Q. (A’, B’) \in S(Q) \)。
设 \( (S’, T’) \in \nu Sₘ \),且 \( \operatorname{\mathtt{treeof}}(S’, T’) = (A’, B’) \)。根据前面证明的 lemma,不妨假设 \( S’ \) 和 \( T’ \) 均不以 \( \mu \) 开头。由于 \( (S’, T’) \in \nu Sₘ \),则 \( (S’, T’) \) 的形式必定如下:
\( (S’, T’) = (S’, \operatorname{\mathtt{Top}}) \),则 \( B’ = \operatorname{\mathtt{Top}} \)。根据 \( S \) 的定义有 \( (A’, B’) \in S(Q) \)
\( (S’, T’) = (S₁ \times S₂, T₁ \times T₂) \),并且 \( (S₁, T₁) \in \nu Sₘ \land (S₂, T₂) \in \nu Sₘ \)。
设 \( Bᵢ = \operatorname{\mathtt{treeof}}(Tᵢ) \),则 \( B’ = \operatorname{\mathtt{treeof}}(T’) = B₁ \times B₂\)。同理有 \( A’ = A₁ \times A₂\)。
由于 \( (S₁, T₁) \in \nu Sₘ \land (S₂, T₂) \in \nu Sₘ \),因此有 \( (A₁, B₁) \in Q \land (A₂, B₂) \in Q \),因此 \((A’, B’) = (A₁ \times A₂, B₁ \times B₂) \in S(Q)\)。
\( (S’, T’) = (S₁ \to S₂, T₁ \to T₂) \) 同理
然后证明必要性。即 \( \operatorname{\mathtt{treeof}}(S, T) \in \nu S \implies (S, T) \in \nu Sₘ \)。同理,设 \( R = \{(S’, T’) \in \mathcal{T}ₘ \times \mathcal{T}ₘ \mid \operatorname{\mathtt{treeof}}(S’, T’) \in \nu S\} \),则 \( (S, T) \in R \)。下面只需要证明 \( R \) 是 \( Sₘ \)-consistent 的即可,即证明 \( \forall (S’, T’) \in R. (S’, T’) \in Sₘ( R) \)。
设 \( \operatorname{\mathtt{treeof}}(S’, T’) = (A’, B’) \in \nu S \),则 \( (A’, B’) \) 一定是下面三种形式之一:\( (A’, \operatorname{\mathtt{Top}}), (A₁ \times A₂, B₁ \times B₂), (A₁ \to A₂, B₁ \to B₂) \)。根据 \( \operatorname{\mathtt{treeof}} \) 的定义,\( (S’, T’) \) 也是这五种形式之一:
\( (S’, T’) = (S’, \operatorname{\mathtt{Top}}) \),显然有 \( (S’, \operatorname{\mathtt{Top}}) \in Sₘ( R) \)
\( S’ = S₁ \times S₂, T’ = T₁ \times T₂ \)
则 \( (A’, B’) = (A₁ \times A₂, B₁ \times B₂) \text{ where } Aᵢ = \operatorname{\mathtt{treeof}}(Sᵢ), Bᵢ = \operatorname{\mathtt{treeof}}(Tᵢ)\)。由于 \( (A’, B’) \in \nu S \),则有 \( (Aᵢ, Bᵢ) \in \nu S \),因此有 \( (Sᵢ, Tᵢ) \in R \)。由于 \( (S’, T’) = (S₁ \times S₂, T₁ \times T₂) \in Sₘ( R) \)
\( S’ = S₁ \to S₂, T’ = T₁ \to T₂ \) 同理
\( (S’, T’) = (S’, \mu X. T₁) \)
令 \( T’’ = [X \mapsto \mu X. T₁]T₁ \),根据 \( \operatorname{\mathtt{treeof}} \) 的定义有 \( \operatorname{\mathtt{treeof}}(T’’) = \operatorname{\mathtt{treeof}}(T’) \)。因此 \( \operatorname{\mathtt{treeof}}(S’, T’’) = \operatorname{\mathtt{treeof}}(S’, T’) \in R \)。由于 \( (S’, T’’) = Sₘ(S’, T’) \),所以 \( (S’, T’) \in Sₘ( R) \)
\( (S’, T’) = (\mu X. S₁, T’) \)
设 \( T’ = \operatorname{\mathtt{Top}} \) 或 \( T’ = \mu Y. T₁ \),则已经被前面的情况包含。否则证明类似上一种情况
这个定理证明了 μ-types 和 regular tree types 之间的等价关系。
Counting Subexpressions
上一节证明了 μ-types 和 regular tree 之间的等价关系,并构建了 μ-types 上的 subtyping 关系。因此可以直接将 \( \operatorname{\mathtt{gfp}}^t \) 的算法套用到 μ-types 上,得到 μ-types 上的 subtyping 算法:
\begin{algorithm} \caption{Subtyping algorithm for μ-types} \begin{algorithmic} \procedure{subtype}{$A, S, T$} \if{$(S, T) \in A$} \return{$A$} \else \state $A_0 \gets A \cup \{(S, T)\}$ \if{$T = \operatorname{\mathtt{Top}}$} \return{$A_0$} \elseif{$S = S_1 \times S_2 \land T = T_1 \times T_2$} \state $A_1 \gets \operatorname{subtype}(A_0, S_1, T_1)$ \return{$\operatorname{subtype}(A_1, S_2, T_2)$} \elseif{$S = S_1 \rightarrow S_2 \land T = T_1 \rightarrow T_2$} \state $A_1 \gets \operatorname{subtype}(A_0, T_1, S_1)$ \return{$\operatorname{subtype}(A_1, S_2, T_2)$} \elseif{$T = \mu X.T_1$} \return{$\operatorname{subtype}(A_0, S, [X \mapsto \mu X.T_1]T_1)$} \elseif{$S = \mu X.S_1$} \return{$\operatorname{subtype}(A_0, [X \mapsto \mu X.S_1]S_1, T)$} \else \state $\operatorname{\mathtt{fail}}$ \endif \endif \endprocedure \end{algorithmic} \end{algorithm}
下面将证明 μ-types 上的 subtyping 关系是 finite-state 的(\( \forall (S, T) \in \mathcal{T}ₘ \times \mathcal{T}ₘ. \text{$\operatorname{\mathtt{reachable_{}}}_{Sₘ}(S, T)$ is finite} \)),从而能够保证在 μ-types 上的 member checking 算法的停机性。
事实上证明这一点有些复杂。有两种方式可以定义在 μ-types 上的 closed subexpressions 的集合:一种是自顶向下的方式,直接从 \( \operatorname{\mathtt{support}}_{Sₘ} \) 中生成集合;另一种是自底向上的方式,用以证明一个 closed μ-tpes 的 closed subexpression 是有穷的。要证明 reachable 集合是有穷的,只要证明前者是后者的子集。
Top-down Subexpression
(top-down subexpression)
A μ-type \( S \) is a top-down subexpression of a μ-type \( T \), written \( S \sqsubseteq T \), if the pair \( (S, T) \) is in the least fixed point of the following generating function:
\begin{aligned} \operatorname{\mathtt{TD}}( R) = {}& \{(T, T) \mid T \in \mathcal{T}_m\} \\ \cup &\ \{(S, T_1 \times T_2) \mid (S, T_1) \in R\} \\ \cup &\ \{(S, T_1 \times T_2) \mid (S, T_2) \in R\} \\ \cup &\ \{(S, T_1 \rightarrow T_2) \mid (S, T_1) \in R\} \\ \cup &\ \{(S, T_1 \rightarrow T_2) \mid (S, T_2) \in R\} \\ \cup &\ \{(S, \mu X.T) \mid (S, [X \mapsto \mu X.T]T) \in R\} \end{aligned}
\[S \sqsubseteq T \overset{\text{def}}{=} (S, T) \in \mu \operatorname{\mathtt{TD}}\]
下面证明 \( \operatorname{\mathtt{support}}_{Sₘ}(S, T)\) 中的元素一定是二者的 top-down subexpression。
If \((S’, T’) \in \operatorname{\mathtt{support}}_{Sₘ}(S, T)\), then either \(S’ \sqsubseteq S\) or \(S’ \sqsubseteq T\), and either \(T’ \sqsubseteq S\) or \(T’ \sqsubseteq T\).
即证明 \((S, T) \in Sₘ(S’, T’) \implies (S’ \sqsubseteq S \lor S’ \sqsubseteq T) \land (T’ \sqsubseteq S \lor T’ \sqsubseteq T)\)。
对 \( \operatorname{\mathtt{support}}_{S_m} \) 的分支进行讨论即可。
If \(S \sqsubseteq U\) and \(U \sqsubseteq T\), then \(S \sqsubseteq T\).
这个命题等价于证明 \( \forall U, T. U \sqsubseteq T \implies (\forall S. S \sqsubseteq U \implies S \sqsubseteq T) \),即证明
\[\mu \operatorname{\mathtt{TD}} \subseteq R = \{(U, T) \mid \forall S. S \sqsubseteq U \implies S \sqsubseteq T\}\]
即证明 \( R \) 是 \( \operatorname{\mathtt{TD}} \)-closed 的,即证明 \( \operatorname{\mathtt{TD}}( R) \subseteq R \)。
设 \( (U, T) \in \operatorname{\mathtt{TD}}( R) \),则有以下几种情况:
\( (U, T) = (T, T) \),显然成立
\( (U, T) = (U, T_1 \times T₂) \) 且 \( (U, T_1) \in R \)
由于 \( (U, T₁) \in R \),因此有 \( \forall S. S \sqsubseteq U \implies S \sqsubseteq T₁ \)。又因为 \( S \sqsubseteq T_1 \implies S \sqsubseteq T_1 \times T₂ \),因此 \( \forall S. S \sqsubseteq U \implies S \sqsubseteq T₁ \times T₂ \),即 \( (U, T₁ \times T₂) \in R \)
其他情况同理
If \((S’, T’) \in \operatorname{\mathtt{reachable}}_{S_m}(S, T)\), then \(S’ \sqsubseteq S\) or \(S’ \sqsubseteq T\), and \(T’ \sqsubseteq S\) or \(T’ \sqsubseteq T\).
由于 \( \operatorname{\mathtt{reachable}}_{Sₘ} \) 是 \( \operatorname{\mathtt{support}}_{Sₘ} \) 的传递闭包,因此对 \( \operatorname{\mathtt{reachable}}_{Sₘ} \) 进行归纳,并利用 \((S’, T’) \in \operatorname{\mathtt{support}}_{Sₘ}(S, T) \implies (S’ \sqsubseteq S \lor S’ \sqsubseteq T) \land (T’ \sqsubseteq S \lor T’ \sqsubseteq T)\) 以及传递规则即可证明。
根据这个命题,想要证明 \( \operatorname{\mathtt{reachable}}_{Sₘ}(S, T) \) 是有穷的,只需要证明任意 μ-type \( U \) 的 top-down subexpression 是有穷的。
一个自然的想法是对 \( U \) 的定义进行归纳,前面几种情况都是显然的,问题在于 \( U = \mu X. T \),根据 \( \operatorname{\mathtt{TD}} \) 的定义,\( (S, \mu X. T) \) 有穷的条件是 \( (S, [X \mapsto \mu X. T]T) \) 是有穷的,但是后者的表达式可能比前者复杂,因此无法直接通过归纳证明这一点。
Bottom-up Subexpression
(bottom-up subexpression)
The μ-type \( S \) is a bottom-up subexpression of a μ-type \( T \), written \( S \preceq T \), if the pair \((S, T)\) is in the least fixed point of the following generating function:
\begin{aligned} \operatorname{\mathtt{BU}}( R) = &\{(T, T) \mid T \in T_m\} \\ \cup\ &\{(S, T_1 \times T_2) \mid (S, T_1) \in R\} \\ \cup\ &\{(S, T_1 \times T_2) \mid (S, T_2) \in R\} \\ \cup\ &\{(S, T_1 \rightarrow T_2) \mid (S, T_1) \in R\} \\ \cup\ &\{(S, T_1 \rightarrow T_2) \mid (S, T_2) \in R\} \\ \cup\ &\{([X \mapsto \mu X.T]S, \mu X.T) \mid (S, T) \in R\} \end{aligned}
Botton-up 和 top-down 的定义的唯一区别在于 \( \mu \) 相关的定义。假设想要收集一个 μ-type \( U = \mu X. T \) 的所有 subexpression,在 top-down 中,会先展开 \( U \),然后收集展开后的式子的子表达式;而在 bottom-up 中,会先收集 body \( T \)(可能不 closed)的子表达式,然后再将其中不 closed 的 \( X \) 替换掉,变回展开后的形式。
\(\{S \mid S \preceq T\}\) is finite for each \(T\).
根据 \( \operatorname{\mathtt{BU}} \) 的定义,容易发现几个事实:
- \( T = \operatorname{\mathtt{Top}} \lor T = x \implies \{S \mid S \preceq T\} = \{T\} \)
- \( T = S₁ \times S₂ \lor T = S₁ \to S₂ \implies \{S \mid S \preceq T\} = \{T\} \cup \{S₁, S₂\} \)
- \( T = \mu X. T’ \implies \{S \mid S \preceq T\} = \{T\} \cup \{[X \mapsto T]S \mid S \preceq T’ \} \)
对 \( T \) 的结构进行归纳即可。
If \(S \preceq [X, Q]T\), then either \(S \preceq Q\) or else \(S = [X, Q]S’\) for some \(S’\) with \(S’ \preceq T\).
对 \( T \) 的结构进行归纳:
\( T = \operatorname{\mathtt{Top}} \)
根据 \( \operatorname{\mathtt{BU}} \) 的定义,只有一种情况 \( (T, T) \),因此 \( S = \operatorname{\mathtt{Top}} \)。令 \( S’ = \operatorname{\mathtt{Top}} \) 即可。
\( T = X \)
则 \( S \preceq [X \mapsto Q] T = Q \)
\( T = Y \ne X \)
同理 \( \operatorname{\mathtt{Top}} \),有 \( S \preceq [X \mapsto Q]T = Y \),因此取 \( S’ = Y \) 即可
\( T = T₁ \times T₂ \)
则 \( S \preceq [X \mapsto Q]T = [X \mapsto Q]T₁ \times [X \mapsto Q]T₂ \)
- 如果 \( S = [X \mapsto Q]T \),同理 \( \operatorname{\mathtt{Top}} \),取 \( S’ = T \) 即可
- 如果 \( S = [X \mapsto Q]T_i \)。根据归纳假设:
- 要么 \( S \preceq Q \),即所证目标
- 要么 \( S = [X \mapsto Q]S’ \) 且 \( S’ \preceq T_i \)。根据 \( \operatorname{\mathtt{BU}} \) 的定义,有 \( S’ \preceq T_1 \times T₂ \),成立
\( T = T₁ \to T₂ \)
同理
\( T = \mu Y. T’ \)
则有 \( S \preceq [X \mapsto Q]T = \mu Y. [X \mapsto Q]T’ \),根据 \( \operatorname{\mathtt{BU}} \) 的定义,有两种可能性
- \( S = [X \mapsto Q] T \),类似于 \( \operatorname{\mathtt{Top}} \) 的情况,有 \( S = \mu Y. [X \mapsto Q]T’ \),取 \( S’ = [X \mapsto Q]T’ \) 即可
- \( S = [Y \mapsto \mu Y.[X \mapsto Q]T’ ]S₁ \) 且 \( S₁ \preceq [X \mapsto Q]T’ \)。根据归纳假设:
要么 \( S₁ \preceq Q \)
根据 substitution 的约束,由于存在 \( \mu Y.[X \mapsto Q]T’ \),因此必须有\( Y \notin \operatorname{\mathtt{FV}}(Q) \)。由于 \( S_1 \preceq Q \),因此必然有 \( Y \notin \operatorname{\mathtt{FV}}(S₁) \),所以 \( S = [Y \mapsto \mu Y.[X \mapsto Q]T’ ]S₁ = S₁ \),所以有 \( S \preceq Q \)。
要么 \( S₁ = [X \mapsto Q]S₂ \) 且 \( S₂ \preceq T’ \)。
则 \( S = [Y \mapsto \mu Y.[X \mapsto Q]T’ ]S₁ = [Y \mapsto \mu Y.[X \mapsto Q]T’ ] [X \mapsto Q]S₂ = [X \mapsto Q] [Y \mapsto \mu Y. T’] S₂ \)。取 \( S’ = [Y \mapsto \mu Y. T’] S₂ \) 即可
If \(S \sqsubseteq T\), then \(S \preceq T\).
原命题等价于证明 \( \mu \operatorname{\mathtt{TD}} \subseteq \mu \operatorname{\mathtt{BU}} \),即证明 \( \mu \operatorname{\mathtt{BU}} \) 是 \( \operatorname{\mathtt{TD}} \)-closed 的。因此只要证明 \( \forall (A, B) \in \operatorname{\mathtt{TD}}(\mu \operatorname{\mathtt{BU}}) \implies (A, B) \in \mu \operatorname{\mathtt{BU}} = \operatorname{\mathtt{BU}}(\mu \operatorname{\mathtt{BU}}) \) 即可。
由于 \( \operatorname{\mathtt{TD}} \) 的大部分 clause 和 \( \operatorname{\mathtt{BU}} \) 的 clause 是一样的,只有最后一条不同,因此只要考虑最后一条即可:
设 \( (A, B) = (S, \mu X. T) \in \operatorname{\mathtt{TD}}(\mu \operatorname{\mathtt{BU}}) \),并且\( (S, [X, \mu X. T] T) \in \mu \operatorname{\mathtt{BU}} \)(即 \( S \preceq [X \mapsto \mu X. T] T \)。根据上一个证明的 lemma,有两种情况:
- 如果 \( S \preceq \mu X. T \),即 \( (A, B) \in \mu \operatorname{\mathtt{BU}} \),成立
- 如果 \( S = [X \mapsto \mu X. T] S’ \) 且 \( S’ \preceq T \)(即 \( (S’, T) \in \mu \operatorname{\mathtt{BU}} \)),根据 \( \operatorname{\mathtt{BU}} \) 最后一条,有 \( (S, \mu X. T) \in \operatorname{\mathtt{BU}}(\mu \operatorname{\mathtt{BU}}) = \mu \operatorname{\mathtt{BU}} \) 成立
综上所述,命题得证。
Finite Reachability
For any μ-types \(S\) and \(T\), the set \(\operatorname{\mathtt{reachable}}_{S_m}(S, T)\) is finite.
对于 μ-types \(S\) 和 \(T\),设 \(\operatorname{\mathtt{Td}}\) 表示它们所有 top-down 子表达式的集合,\(\operatorname{\mathtt{Bu}}\) 表示它们所有 bottom-up 子表达式的集合。
前面已经证明几个事实:
- \(\operatorname{\mathtt{reachable}}_{S_m}(S, T) \subseteq \operatorname{\mathtt{Td}} \times \operatorname{\mathtt{Td}}\)
- \(\operatorname{\mathtt{Td}} \times \operatorname{\mathtt{Td}} \subseteq \operatorname{\mathtt{Bu}} \times \operatorname{\mathtt{Bu}}\)
- \(\operatorname{\mathtt{Bu}} \times \operatorname{\mathtt{Bu}}\) 有穷
\(\operatorname{\mathtt{reachable}}_{S_m}(S, T)\) 有穷。
此外,从上面的定理可以看出为了检验 \( (S, T) \),那么其 reachable 将是与 subexpressions 数量的平方成正比的。
An Exponential Algorithm
上面的算法有个变体:如果不记录中间的检查结果,令函数返回布尔值,那么这个算法的复杂度是指数级的。
\begin{algorithm} \caption{Subtyping algorithm for ac-types} \begin{algorithmic} \procedure{subtype-ac}{$A, S, T$} \if{$(S, T) \in A$} \return{\texttt{true}} \else \state $A_0 \gets A \cup \{(S, T)\}$ \if{$T = \operatorname{\mathtt{Top}}$} \return{\texttt{true}} \elseif{$S = S_1 \times S_2 \land T = T_1 \times T_2$} \return{$\operatorname{subtype-ac}(A_0, S_1, T_1) \land \operatorname{subtype-ac}(A_0, S_2, T_2)$} \elseif{$S = S_1 \rightarrow S_2 \land T = T_1 \rightarrow T_2$} \return{$\operatorname{subtype-ac}(A_0, T_1, S_1) \land \operatorname{subtype-ac}(A_0, S_2, T_2)$} \elseif{$S = \mu X.S_1$} \return{$\operatorname{subtype-ac}(A_0, [X \mapsto \mu X.S_1]S_1, T)$} \elseif{$T = \mu X.T_1$} \return{$\operatorname{subtype-ac}(A_0, S, [X \mapsto \mu X.T_1]T_1)$} \else \return{\texttt{false}} \endif \endif \endprocedure \end{algorithmic} \end{algorithm}
可以通过下面的例子来观察它的复杂度。考虑 \( S_n, Tₙ \):
\[S₀ = \mu X. \operatorname{\mathtt{Top}} \times X\] \[S_{n+1} = \mu X. X \to Sₙ\] \[T₀ = \mu X. \operatorname{\mathtt{Top}} \times (\operatorname{\mathtt{Top}} \times X)\] \[T_{n+1} = \mu X. X \to Tₙ\]
其中 \( S_n, T_n \) 都是线性增长的。但是考虑计算 \( \operatorname{\mathtt{subtype}}^{ac} (\emptyset, S_n , T_n ) \):
\begin{aligned} &\operatorname{\mathtt{subtype}}^{ac}(\emptyset, S_n, T_n) \\ =&\ \operatorname{\mathtt{subtype}}^{ac}(A_1, S_n \rightarrow S_{n-1}, T_n) \\ =&\ \operatorname{\mathtt{subtype}}^{ac}(A_2, S_n \rightarrow S_{n-1}, T_n \rightarrow T_{n-1}) \\ =&\ \operatorname{\mathtt{subtype}}^{ac}(A_3, T_n, S_n) \land \underline{\operatorname{\mathtt{subtype}}^{ac}(A_3, S_{n-1}, T_{n-1})} \\ =&\ \operatorname{\mathtt{subtype}}^{ac}(A_4, T_n \rightarrow T_{n-1}, S_n) \land \dots \\ =&\ \operatorname{\mathtt{subtype}}^{ac}(A_5, T_n \rightarrow T_{n-1}, S_n \rightarrow S_{n-1}) \land \dots \\ =&\ \operatorname{\mathtt{subtype}}^{ac}(A_6, S_n, T_n) \land \underline{\operatorname{\mathtt{subtype}}^{ac}(A_6, T_{n-1}, S_{n-1})} \land \dots \\ =& \dots \\ \text{where} & \\ A_1 &= \{(S_n, T_n)\} \\ A_2 &= A_1 \cup \{(S_n \rightarrow S_{n-1}, T_n)\} \\ A_3 &= A_2 \cup \{(S_n \rightarrow S_{n-1}, T_n \rightarrow T_{n-1})\} \\ A_4 &= A_3 \cup \{(T_n, S_n)\} \\ A_5 &= A_4 \cup \{(T_n \rightarrow T_{n-1}, S_n)\} \\ A_6 &= A_5 \cup \{(T_n \rightarrow T_{n-1}, S_n \rightarrow S_{n-1})\}. \end{aligned}
注意这里每次计算 \( (Sₙ, T_n) \) 都会需要重复 \( (S_{n-1}, T_{n-1}) \) 以及 \( (T_{n-1}, S_{n-1}) \) 的计算。因此这个算法的复杂度是指数级的。
Subtyping Iso-Recursive Types
最后考虑 iso-recursive types 的 subtyping 关系。由于在 iso-recursive 中折叠是通过 fold 和 unfold 操作显式进行的,因此可以明确定义 iso-recursive types 的 subtyping 规则。
最常见的 Iso-recursive subtyping 规则是 Amber 语言中介绍的:
\[\frac{\Sigma, X \colon Y \vdash S <: T}{\Sigma \vdash \mu X.S <: \mu Y.T} \tag{S-Amber}\]
\[\frac{(X <: Y) \in \Sigma}{\Sigma \vdash X <: Y} \tag{S-Assumption}\]
这里的 \( \Sigma \) 是 a set of pairs of recursion variables,用于记录递归变量的自类型关系,类似 \( \Gamma \)。并且在使用这条规则时,要求先将两侧的递归变量命名为不同的名字,否则这条规则就没有意义了。
实际上,如果把这两条规则加入到前面章节中介绍的不包含 recursive types 的 subtyping 算法中,那么会得到一个类似 \( \operatorname{\mathtt{subtype}}^{ac} \) 的算法(但是不会做递归变量的替换,并且两侧的递归类型会同时展开)。其中 \( \Sigma \) 对应了算法中的 \( A \),记录比较过程中遇到的递归变量。