如果一个类型定义中包含了自身,那么这种类型称为recursive types。例如 NatList 的定义中,要么是 Nil,要么是 Cons Nat NatList:
\[ \operatorname{\mathtt{NatList}} = \langle \operatorname{\mathtt{nil}}: \operatorname{\mathtt{Unit}}, \operatorname{\mathtt{cons}}: \{\operatorname{\mathtt{Nat}}, \operatorname{\mathtt{NatList}}\} \rangle \]
这个递归式定义了一个无穷的树类型:
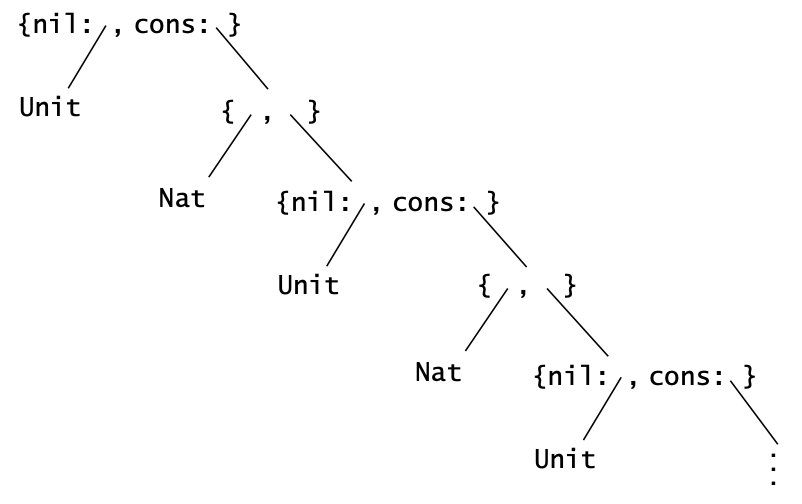
Figure 1: Natlist
这里在一个类型定义中出现了正在定义的类型自身,类似前面介绍的 fix 组合子。因此为了能让这个定义成立,模仿 fix 的定义引入递归算子 \( \mu \):
\[ \operatorname{\mathtt{NatList}} = \mu X. \langle \operatorname{\mathtt{nil}}: \operatorname{\mathtt{Unit}}, \operatorname{\mathtt{cons}}: \{\operatorname{\mathtt{Nat}}, X\} \rangle \]
通过这种方式就可以定义 recursive types 而无需给它命名。其含义为是:NatList 是满足方程 X = <nil: Unit, cons: {Nat, X}> 的无穷类型。
有两种形式化 recursive types 的方式:equi-recursive 和 iso-recursive。它们作为 typechecker 时需要的类型标注不同。后面的例子会使用较为简单的 equi-recursive。
Examples
List
为了定义 NatList,需要定义 constructor nil 和 cons,isnil 以及两个 destructor hd 和 tl。这里利用 variant type(使用的形式为 \( \langle l = t \rangle\ \operatorname{\mathtt{as}}\ T \))来定义 NatList:
nil = <nil = unit> as NatList;
(** nil: NatList *)
cons = λn: Nat. λl: NatList. <cons = {n, l}> as NatList;
(** cons : Nat → NatList → NatList *)
isnil = λl: NatList.
case l of
<nil = u> ⇒ true
| <cons = p> ⇒ false;
(** isnil : NatList → Bool *)
hd = λl: NatList.
case l of
<nil = u> ⇒ 0
| <cons = p> ⇒ p.1;
(** hd : NatList → Nat *)
tl = λl: NatList.
case l of
<nil = u> ⇒ l
| <cons = p> ⇒ p.2;
(** tl : NatList → NatList *)
为了不考虑异常,这里将空列表的 hd 定义为 0,将空列表的 tl 定义为空列表。
利用这些定义,可以写一个求和的函数:
sumlist = fix (λs: NatList → Nat. λl: NatList.
if isnil l then 0 else plus (hd l) (s (tl l)));
(** sumlist : NatList → Nat *)
虽然 NatList 是一个无穷类型,但是它的所有 terms 都是有穷列表。
Stream
定义一个函数,它会接受一个 Nat 然后返回自己。这样的函数可以无限接收参数:
Hungry = μA. Nat → A;
f = fix (λf: Nat → Hungry. λn: Nat. f);
(** f : Hungry *)
(** f 0: Hungry; *)
(** f 0 1: Hungry; *)
这个函数的变种是 Stream 类型,它能接受任意数量的 unit,然后返回一个 Nat 和一个新的 Stream:
Stream = μA. Unit → {Nat, A};
Stream 可以定义两个 destructor,分别用于取出 Nat 和 Stream:
hd = λs: Stream. (s unit).1;
(** hd : Stream → Nat *)
tl = λs: Stream. (s unit).2;
(** tl : Stream → Stream *)
可以用 fix 来构建一个 Stream,返回一个无穷递增序列。考虑 Steam 实际上是一个函数,它返回这个 Nat 和一个 Nat + 1 的函数(Stream),因此应当写一个函数:每次接受一个 Nat,然后利用它构造函数(Stream):
upfrom0 = fix (λf: Nat → Stream. λn: Nat. λ_: Unit. {n, f (succ n)}) 0;
(** upfrom0 : Stream *)
hd (tl (tl (tl upfrom0)));
(** 3 : Nat *)
Stream 可以被扩展成一个 Process:接受一个 Nat,然后返回一个 Nat 和一个新的 Process:
Process = μA. Nat → {Nat, A};
例如一个每次返回所有接收到的数字之和的 Process:
p = fix (λf: Nat → Process. λacc: Nat. λn: Nat.
let newacc = plus acc n in
{newacc, f newacc}) 0;
(** p : Process *)
curr = λs:Process. (s 0).1;
(** curr : Process → Nat *)
send = λn: Nat. λs: Process. (s n).2;
(** send : Nat → Process → Process *)
curr (send 20 (send 3 (send 5 p)));
(** 28: Nat *)
Objects
利用 recursive types 可以定义纯函数式的对象(先前都是使用 Ref 定义的)。例如一个 Counter 对象,使用 inc 方法时会返回一个新的 Counter:
Counter = μC. {get: Nat, inc: Unit → C};
可以发现 Process 和 Objects 的定义很像,唯一的区别是 Objects 接收一个 record type 作为 fields,并且方法也是一个 record type。
Counter = μC. {get: Nat, inc: Unit → C};
c = let create = fix (λf: {x: Nat} → Counter. λs: {x: Nat}.
{ get = s.x,
inc = λ_: Unit. f {x = succ(s.x)})
in create {x = 0};
(** c : Counter *)
c1 = c.inc unit;
c2.get;
(** 1 : Nat *)
Recursive values
利用 recursive types 可以定义 well-typed fix-point combinator:
\[ \operatorname{\mathtt{fix}}_T \underline{: (T \to T) \to T} = \lambda f: T \to T. (\lambda x: (\mu A. A \to T). f\ (x\ x))\ (\lambda x: \mu (\mu A. A \to T). f\ (x\ x)) \]
如果忽略掉类型,那么这个定义就是 UTLC 中的 fix-point combinator。
这个定义的技巧在于 x 的类型:对于表达式 \( x\ x \),因此 \( x \) 一定是箭头类型(函数),它的参数是 \( x \) 自身。显然这一定是一个无穷类型,而 \( \mu A. A \to T \) 则符合这个条件。
这个定义的一个推论是 recursive types 会破坏 strong normalization property。因为这个 fix-point combinator 可以定义一个不会停机的函数:
\[ \operatorname{\mathtt{diverge}}_T \underline{: \operatorname{\mathtt{Unit}} \to T} = \lambda \_: \operatorname{\mathtt{Unit}}. \operatorname{\mathtt{fix}}_T\ (\lambda x: T. x) \]
利用 diverge 可以为任意类型构造一个 term \( \operatorname{\mathtt{diverge}}_T\ \operatorname{\mathtt{unit}} \)。因此包含 recusive tpes 的 logic system 是 inconsistent 的。
UTLC
利用 recursive types 可以在 STLC 中嵌入 UTLC,并且确保类型安全。
首先定义一个类型 \( D \)(此处的定义就是 denotational semantics 中 UTLC 的 universal domains 的 property 定义):
D = μX. X → X;
定义一个 injection function lam 来将 \( D \to D \) 转换为 \( D \):
lam = λf: D → D. f as D;
(** lam : D *)
为了构造 application,只需要将第一个函数展开成函数,然后将第二个函数应用到它上:
ap = λf: D. λx: D. f x;
(** ap : D *)
假设 \( M \) 是一个 UTLC 上的 closed term,那么可以用下面的方式构造一个 \( M* : D \) 来表示 \( M \):
x* = x
(λx.M)⋆ = lam (λx: D. M⋆)
(MN)⋆ = ap M⋆ N⋆
下面是 fix-pointer 的例子:
fixD = lam (λf:D.
ap (lam (λx:D. ap f (ap x x)))
(lam (λx:D. ap f (ap x x))));
(** fixD : D *)
此外,可以向这套系统中加入其他类型,例如 Nat:
D = μX. <nat: Nat, fn: X → X>;
lam = λf:D → D. <fn = f> as D;
(** lam : (D → D) → D *)
ap = λf: D. λa: D.
case f of
<nat = n> ⇒ divergeD unit
| <fn = f> ⇒ f a;
(** ap : D → D → D *)
suc = λf: D.
case f of
<nat = n> ⇒ (<nat = succ n> as D)
| <fn = f> ⇒ divergeD unit;
(** suc : D → D *)
zro = <nat = 0> as D;
(** zro : D *)
这里处理了一种异常情况:如果 \( f \) 是一个 nat,那么 ap 就会返回一个不会停机的函数表示异常。这种检查类似于动态类型语言的运行时检查。有趣的是将 if 编码进去:
D = μX. <nat: Nat, bool: Bool, fn: X → X>;
lam = λf: D → D. <fn = f> as D;
ap = λf: D. λa: D.
case f of
<nat = n> ⇒ divergeD unit
| <bool = b> ⇒ divergeD unit
| <fn = f> ⇒ f a;
ifd = λb: D. λt: D. λe: D.
case b of
<nat = n> ⇒ divergeD unit
| <bool = b> ⇒ (if b then t else e)
| <fn = f> ⇒ divergeD unit;
tru = <bool = true> as D;
fls = <bool = false> as D;
ifd fls one fls;
(** false 注意这里两个分支返回了不同的类型 *)
Formalities
有两种方式可以处理 recursive types:equi-recursive 和 iso-recursive。他们的区别在于:Recursive type \( \mu X.T \) 和它的一步展开的关系。
Equi-recursive
在 equi-recursive 中,recursive type 和它的展开是相等的,也就是说两者可以在任意情况下互换,它们表示相同的无穷结构,typechecker 需要确保左右可以互换。
Equi-recursive 的好处在于它只在现有的类型系统上添加了一个小修改:允许类型表达式是无穷的。这样原有的定义和证明中的那些不依赖于在类型表达式上进行归纳的部分就不需要修改了(因为类型表达式是无穷的,因此不能自下而上归纳)。
但是实现 equi-recursive 需要处理无穷结构,因此需要额外工作。
Iso-recursive
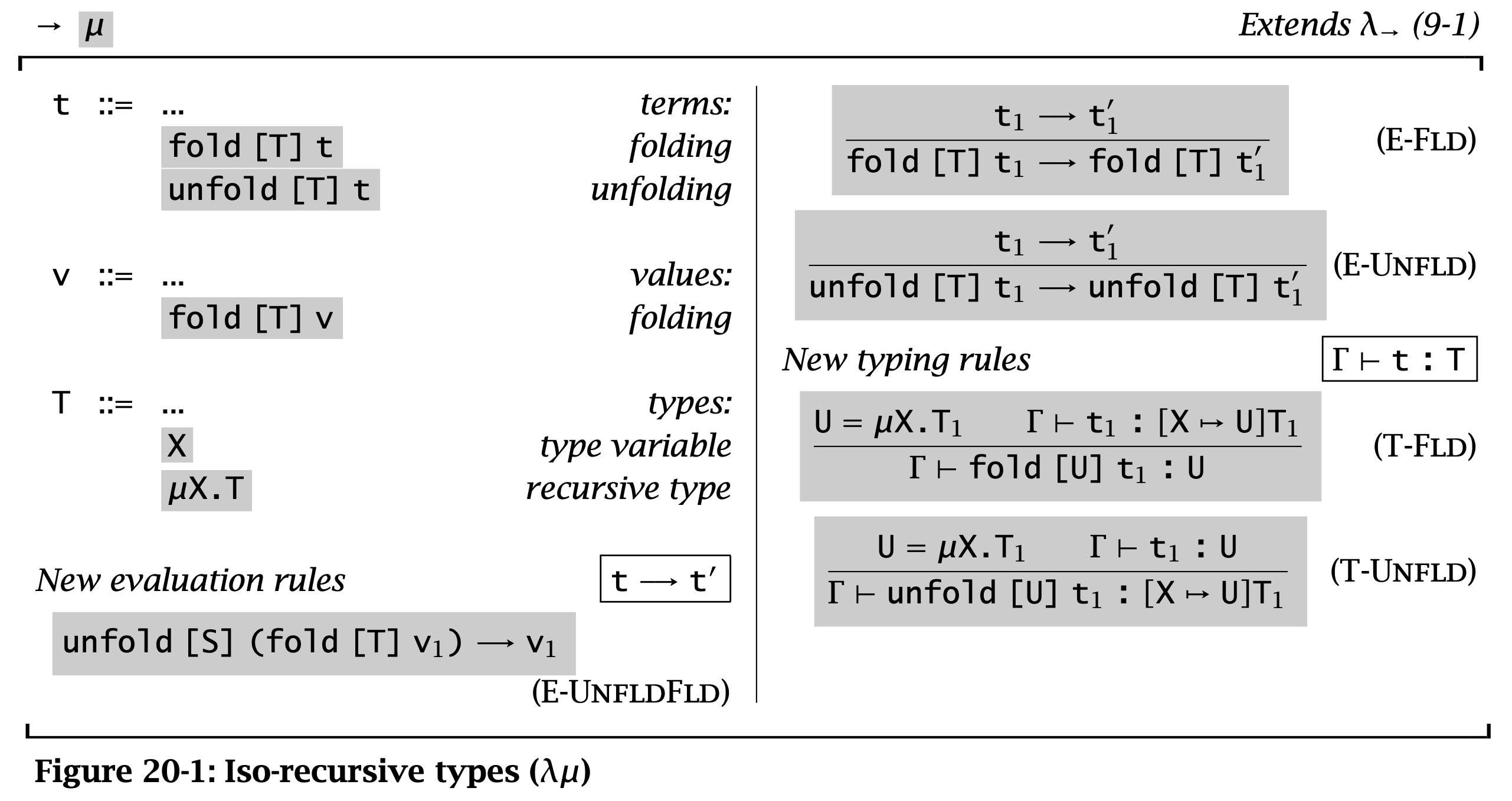
Figure 2: Iso-recursive
Iso-recursive 则将 recursive type 和其展开看作是不同但是可以相互转换的类型。
在 iso-recursive 中,类型 \( \mu X.T \) 的展开是将 body \( T \) 中的 \( X \) 替换为 \( \mu X.T \),即 \( [X \mapsto (\mu X. T)]T \)。
在 iso-recursive 中,对于每个 recursive type \( \mu X. T \) 会引入一对函数:
\[ \operatorname{\mathtt{unfold}}[\mu X. T]: \mu X. T \to [X \mapsto (\mu X. T)]T \]
\[ \operatorname{\mathtt{fold}}[\mu X. T]: [X \mapsto (\mu X. T)]T \to \mu X. T \]
这两对函数表述了这种“同构”:
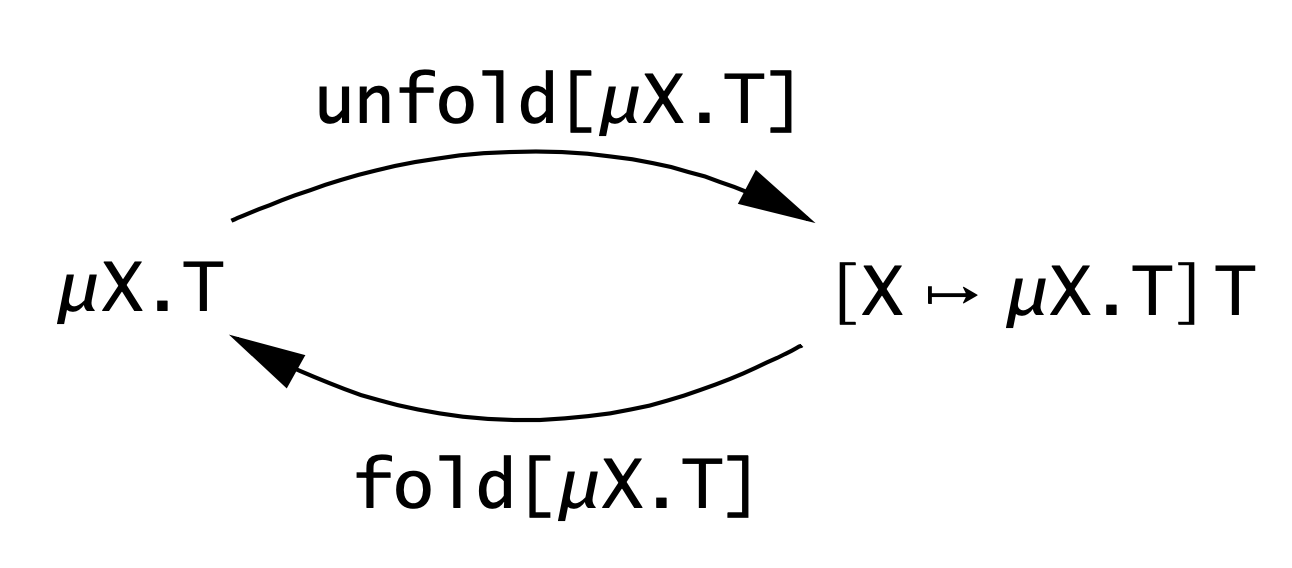
Figure 3: Fold and Unfold
在 iso-recursive 中,fold 和 unfold 是 primitives,它们的关系由 E-UnfldFld 保证。这里不要求 fold 和 unfold 上的类型标注必须相同(S 和 T),因为这需要运行期检查。但是在一个 well-typed 的程序中只要使用了 UnfldFld,那么这两个类型标注一定相等的。
Summary
从上面可以看出,equi-recursive 更加直观,但是它需要 typechecker 推断出需要 fold 和 unfold 的地方以处理无穷类型;此外,equi-recursive 和其他高级的类型系统特性(例如 bounded quantification 和 type operators)交互会更复杂,甚至有可能是一个 undecidable 的问题(typechecker 不停机)。
而 iso-recursive 写起来更麻烦,需要在程序中显式使用 fold 和 unfold,但是它的类型检查更加简单。但是在使用中,这两个 primitives 可以和其他特性相合并:例如在 ML 中,每次使用 datatype 都隐式引入了 recursive types。每次使用 constructor 构造一个值时,都会隐式使用 fold,而每次在模式匹配中出现 constructors 时都会隐式使用 unfold;在 Java 中,每个 class 的定义都使用了 recursive types,因此每个类的定义都会使用 fold,而每个对 objects 的方法调用都使用了 unfold。
下面是 iso-recursive 定义的例子:
NatList = μX. <nil: Unit, cons: {Nat, X}>;
NLBody = <nil: Unit, cons: {Nat, NatList}>;
nil = fold[NatList] (<nil = unit> as NatList);
cons = λn: Nat. λl: NatList. fold[NatList] (<cons = {n, l}> as NatList);
isnil = λl: NatList.
case unfold [NatList] l of
<nil=u> ⇒ true
| <cons=p> ⇒ false;
hd = λl: NatList.
case unfold [NatList] l of
<nil=u> ⇒ 0
| <cons=p> ⇒ p.1;
tl = λl: NatList.
case unfold [NatList] l of
<nil=u> ⇒ l
| <cons=p> ⇒ p.2;
fixT =
λf: T → T.
(λx: (μA. A → T). f ((unfold [μA. A → T] x) x))
(fold [μA. A → T] (λx: (μA. A → T). f ((unfold [μA. A → T] x) x)));
Subtyping
下面讨论 subtyping 和 recursive types 的结合。
考虑两个类型:\( A = \mu X. \operatorname{\mathtt{Nat}} \to (\operatorname{\mathtt{Even}} \times X) \) 和 \( B = \mu X. \operatorname{\mathtt{Even}} \to (\operatorname{\mathtt{Nat}} \times X) \),其中 \( \operatorname{\mathtt{Even}} <: \operatorname{\mathtt{Nat}} \)。
为了方便起见,这里使用 equi-recursive。从类型定义可以看出,这两个类型可以看作两个会互相交互的 process:给定一个数字,它会返回另一个数字,以及一个 \( A \) 能接受任意数字,并返回一个偶数;而 \( B \) 能接受偶数,并返回一个数字。因此所有用到 \( B \) 的地方都可以用 \( A \) 替代,所以 \( A <: B \)。
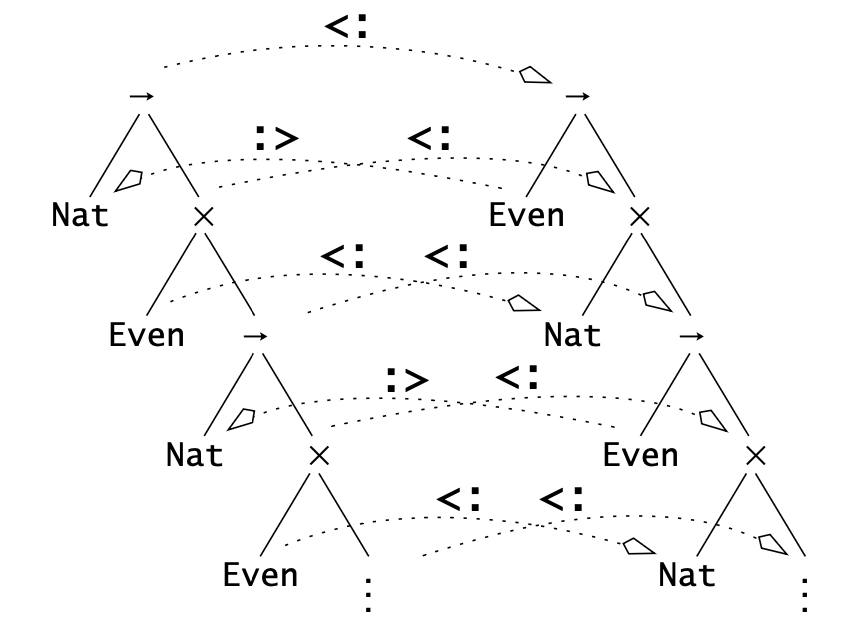
Figure 4: Subtyping and recursive types
下一章会严格定义 recursive types + subtyping 的规则。