Overview
Featherweight Java (FJ) 是一个建模 Java 类型系统的计算模型,它忽略了并发、反射等特性,只考虑 object creation, method invocation, field access, casting 以及 variables。FJ 的一个关键简化是不考虑赋值操作,假设对象的字段都由构造函数初始化,不会再改变,这样将其限制在一个 FP 的场景下。
为了保证一致性,FJ 中的类都有父类(即使是 Object),都有构造函数,并且在字段访问或者方法调用中总是指出接收者(即使是 this)。并且假设构造函数的格式是固定的:每个参数都对应一个字段,并且字段名和参数名相同,参数顺序和字段声明顺序相同;构造函数会先调用父类构造函数来初始化父类;只有在构造函数中允许出现 super 和赋值。
由于 FJ 不支持副作用,因此方法体必须是 return Expr 的形式。
class A extends Object { A() { super(); } }
class B extends Object { B() { super(); } }
class Pair extends Object {
Object fst;
Object snd;
// Constructor:
Pair(Object fst, Object snd) {
super(); this.fst=fst; this.snd=snd; }
// Method definition:
Pair setfst(Object newfst) {
return new Pair(newfst, this.snd); } }
在 FJ 中,term 共有五种基本形式:
- object constructors:
new C(e1, ..., en) - method invocation:
e0.m(e1, ..., en) - field access:
e0.f,this.f - variables:
x - casting:
(Pair) new Pair(new A(), new B())
去除副作用后,对于程序的评估可以直接在 FJ 中进行,而不需要建模 heap。FJ 有三条基本的计算规则,分别用于 field access, method invocation 和 casting。在 lambda calculus 中对于 application 的 evaluating 规则会先假设函数已经化简为一个 abstraction,而在 FJ 中会假设被操作的对象被化简为一个 new term:everything is an object.
E-ProjNew: \(\operatorname{\mathtt{new}} \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ B()).\operatorname{\mathtt{snd}} \rightarrow \operatorname{\mathtt{new}}\ B()\)E-InvkNew:\begin{align*} & \operatorname{\mathtt{new}} \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ B()).\operatorname{\mathtt{setfst}}(\operatorname{\mathtt{new}}\ B()) \\ \rightarrow {}& [ \operatorname{\mathtt{newfst}} \mapsto \operatorname{\mathtt{new}}\ B(), \operatorname{\mathtt{this}} \mapsto \operatorname{\mathtt{new}}\ \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ B()) ] \operatorname{\mathtt{new}}\ \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{newfst}}, \operatorname{\mathtt{this}}.\operatorname{\mathtt{snd}}) \\ \rightarrow {}& \operatorname{\mathtt{new}} \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ B()).\operatorname{\mathtt{snd}}) \end{align*}
E-CastNew: \((\operatorname{\mathtt{Pair}})\operatorname{\mathtt{new}}\ \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ B()) \rightarrow \operatorname{\mathtt{new}}\ \operatorname{\mathtt{Pair}}(\operatorname{\mathtt{new}}\ A(), \operatorname{\mathtt{new}}\ B())\)
分别对应着有三种情况可能导致 stuck:
- 访问一个不存在的字段
- 调用一个不存在的方法
- 尝试将一个对象转换为非父类的类型
后面会证明在类型安全的程序中,这三种情况都不会发生(除了错误的强制转换)。
Nomianal and Structural Typing
本书介绍 lambda 演算的时候会使用名称来表示一些复杂的类型,例如 NatPair = {fst: Nat, snd: Nat},但是两者之间是可以互换的,没有任何区别。
而在 Java 等语言中,类型的名字非常重要。Java 中的每个复合类型都必须有一个名称,并且在声明或者定义变量时要使用类型名称,而不能直接使用 {fst: Nat, snd: Nat} 这样的结构。这样的设计使得程序员需要在定义类型时,明确声明这个类型扩展了哪些类或者接口,并且编译器会对其进行检查。Java 的 subtyping 被定义为声明的直接 subtyping 的自反和传递闭包。尽管一个类在结构上是另一个类的子类,但是如果没有明确声明,那么这两个类之间并没有 subtyping 关系。
Java 这样的强调类型名称、subtyping 关系需要明确声明的系统称为 nominal typing,而只关注结构、subtyping 关系直接定义在类型结构上的称为 structural typing。
Nominal typing (NT) 的优点如下:
类型名称可以用于运行时的类型检查。NT 可以在运行时对象上增加一个包含类型名称的 tag,这相当于一个指针,指向了这个类型的运行时数据结构。这个数据结构可以包含指向其直接父类的指针。利用这点可以进行运行时的类型检查(例如
instanceof)、打印数据结构、序列化、反射等。虽然 ST 也可以实现运行时的类型标记,但是这不像 NT 中运行时 tag 和编译期是一致的。NT 上定义 recursive type 是 free 的:即在定义中使用了自身名字的类型,同时 NT 定义互递归类型也很直观,因为只是名字的问题;而在 ST 上严格处理 recursive type 则会麻烦一些。这里的 recursive type 指的是类中的方法签名引用所在类签名的情况,例如
class C { }。NT 上检查一个类型是否为另一个类型的 subtype 非常简单,因为只需要在类型定义的时候检查一次即可;而在 ST 上则需要在每个类型出现的地方都检查一次。因此 NT 上的类型检查更简单。但是在复杂的编译器中二者在这点上差异不大,因为 ST 也可以实现让 subtyping 检查只进行一次。
最后 NT 可以避免“虚假包含”。因为在实际工程中可能出现一种情况,两种类型虽然结构上相同,但是在含义上是不同的。不过这个优势也不明显,因为 ST 中可以使用单 constructor 类型(
newtype)或者 ADT 来避免这点。
虽然 NT 在工业语言里面更常用,但是 PL 相关的文献几乎都集中在 ST 中。这是因为如果没有 recursive type,那么 ST 更加简洁和优雅,因为 ST 中的类型表达式是一个封闭的实体,而 NT 需要考虑类型名称的定义。
并且很多高级的类型抽象特性(例如 parametric polymorphism, user-defined operator)等不适合 NT。例如 List[T] 之类的泛型也是一种 ST,因为它是类型的复合,但是在 NT 下就要求给它一个特定的名称,但是我们又没法给泛型一个特定的名称(那样就不能带参数了)。也有一些工作在 NT 下实现了这些特性,但是它们几乎都在这些特性上引入了 ST。因此具有高级类型特性的语言会更倾向于 ST。
Inheritance and Subtyping
首先定义什么叫 inheritance,可以理解为代码复用。
在 ST 中,继承被表述为 \(C = \lambda \operatorname{\mathtt{self}}. P(\operatorname{\mathtt{self}}) + \{\overline{m} = \overline{t}\}\)。这里使用 \( P(\operatorname{\mathtt{self}}) \) 是为了实现 open recursion。
然后考虑一种特殊情况:ST 中如何使用自引用(引用所在类的类型的方法)。由于在 ST 中没有名字,因此只能使用类似上一章介绍的 fix-point 来定义对象:
设 \( P = \lambda \operatorname{\mathtt{self}}. r \),则对象为 \( p = \operatorname{\mathtt{fix}}\ P \)。如果 \( p: \sigma \),则 \( P: \sigma \rightarrow \sigma \)。
当继承和自引用同时出现时,结果就是
\[ C = \lambda \operatorname{\mathtt{self}}. P(\operatorname{\mathtt{self}}) + \{\overline{m} = \overline{t}\} \\ c = \operatorname{\mathtt{fix}} (\lambda \operatorname{\mathtt{self}}. P(\operatorname{\mathtt{self}}) + \{\overline{m} = \overline{t}\}) \]
这里 \( c: \tau = \sigma + \{\overline{m}: \overline{T}\} \)。
设 \( P = \lambda \operatorname{\mathtt{self}}. \{f: \operatorname{\mathtt{self}} \rightarrow \operatorname{\mathtt{Unit}}\} \)。然后定义继承的类 \( C = \lambda \operatorname{\mathtt{self}}. P(\operatorname{\mathtt{self}}) + \{t\} \)。此时分别构建子类和父类的对象,会得到 \(p = \operatorname{\mathtt{fix}}\ P: \sigma\),\( c = \operatorname{\mathtt{fix}}\ C: \tau \)。问题是:“这两个对象之间存在 subtyping 关系吗,即 \( \tau <: \sigma \) 吗?”
假设 \( \tau <: \sigma \)。由于 \( c.f \) 是由 \( P(\operatorname{\mathtt{self}}: \tau) \) 构建的,因此有 \( c.f : \tau \rightarrow \operatorname{\mathtt{Unit}} \)。而 \( p.f: \sigma \rightarrow \operatorname{\mathtt{Unit}} \),因为函数参数是逆变的,因此有 \( \sigma \rightarrow \operatorname{\mathtt{Unit}} <: \tau \rightarrow \operatorname{\mathtt{Unit}} \)。这违反了 subtyping 关系:所有用到 \( p.f \) 的地方不能用 \( c.f \) 代替,而是要反过来。因此产生了矛盾,所以这两个对象之间不存在 subtyping 关系。
因此在 ST 中,subtyping 和 inheritance 是正交的概念;而在 NT 中不存在这个问题,因为可以用 nominal typing 直接指定类型名称,有工作利用 denotational semantics 上证明了 subtyping 意味着 inheritance。
Definition
Syntax
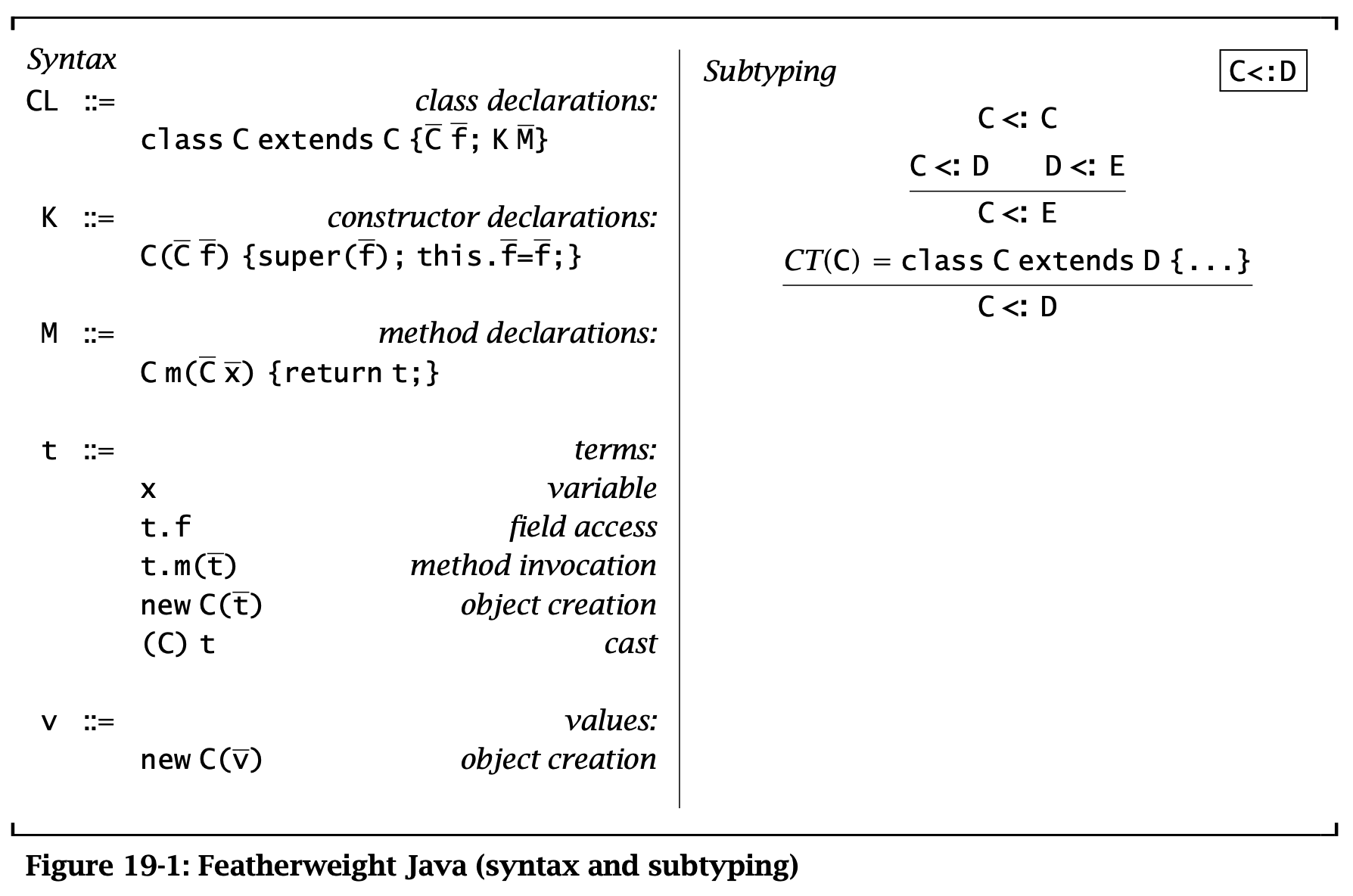
Figure 1: Featherweight Java (syntax and subtyping)
FJ 的语法定义如图,其中 this 是一个特殊变量,表示当前对象,但是不在方法参数中使用。这里 \(\overline{C}\) 是一种简写,表示一个序列 \(C_1, C_2, \dots, C_n\)。
Class declaration \(\operatorname{\mathtt{class}}\ C\ \operatorname{\mathtt{extends}}\ D\ \{\overline{C}\ \overline{f}; K\ \overline{M}\}\) 声明了一个继承自 \(D\) 的类 \(C\),其中 \(f\) 是字段,\(K\) 是构造函数,\(\overline{M}\) 是方法。其中 \(C\) 中添加的字段和方法不应该和 \(D\) 中继承的重名。
Constructor declaration \(C(\overline{D}\ \overline{g}, \overline{C}\ \overline{f})\ \{\operatorname{\mathtt{super}}(\overline{g}); \operatorname{\mathtt{this}}.\overline{f} = \overline{f}\}\) 声明了一个构造函数。构造函数接受两方面的参数:父类的构造函数参数和自己的字段初始化参数。构造函数中首先调用父类的构造函数,然后初始化自己的字段。
Method declaration \(D\ m(\overline{C}\ \overline{x}) \{\operatorname{\mathtt{return}}\ t;\}\) 声明了一个方法。方法接受参数 \(\overline{x}\),返回一个表达式 \(e\),变量 \(x\) 和 \(\operatorname{\mathtt{this}}\) 都可以在 \(x\) 中使用。
Class table \(CT\) 是一个从类名到类定义的映射。
每一个类都有通过 extends 声明的父类,其中 Object 是所有类的父类,这里将其视作一个特殊的类,不出现在类表中。查找类表中的 Object 的字段时直接返回 \(\cdot\),同时 Object 也没有任何方法。因此每个类都是 Object 的 subtype。
通过类表可以推断类之间的 subtyping 关系。类表满足一些合理的条件:
- \(\forall C \in \operatorname{\mathrm{dom}}(CT). CT( C) = \operatorname{\mathtt{class}}\ C \dots\)
- \(\operatorname{\mathtt{Object}} \notin \operatorname{\mathrm{dom}}(CT)\)
- \(\forall \operatorname{\mathrm{name}}\ C \in CT. C \in \operatorname{\mathrm{dom}}(CT)\)
- \(CT\) 中的 subtyping 关系没有循环,即 subtyping 关系是反对称的
类型可以有互相定义(即类 A 中有类型为 B 的字段,同时类 B 中有类型为 A 的字段),或者类 \(A\) 中有类型为 \(A\) 的字段。
Auxiliary Definitions
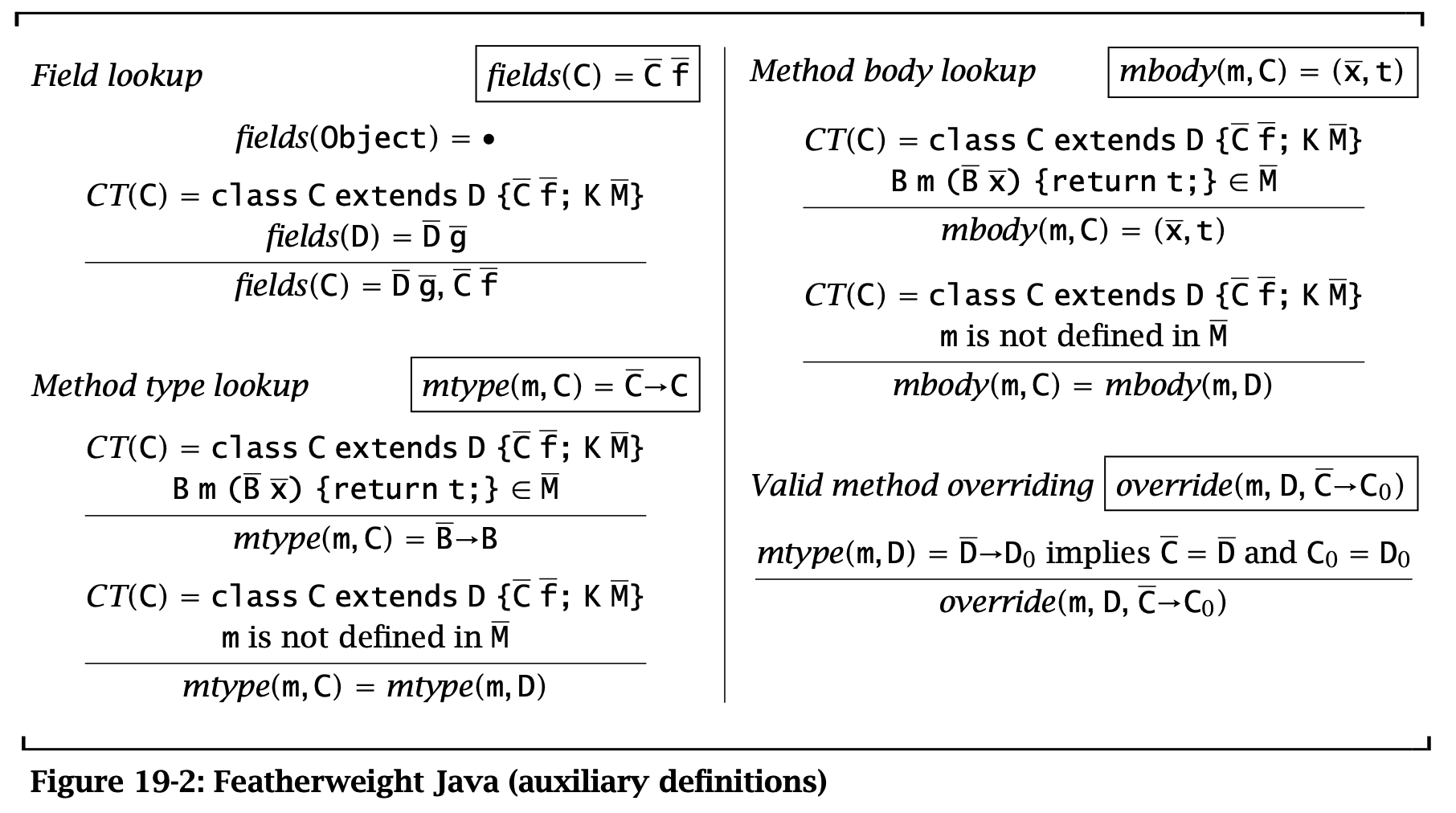
Figure 2: Featherweight Java (Auxiliary Definitions)
为了定义类型检查和 evaluation 规则,这里需要一些辅助定义。
\(\operatorname{\mathtt{field}}( C)\) 会返回类 \(C\) 及其父类中的所有字段及其所在类。
\(\operatorname{\mathtt{mtype}}(m, C)\) 会返回类 \(C\) 中方法 \(m\) 的类型 \(B \rightarrow B\)。\(\operatorname{\mathtt{mbody}}(m, C)\) 会返回类 \(C\) 中方法 \(m\) 的定义,返回 \((x, t)\),分别表示 \(m\) 的参数和方法体。
谓词 \(\operatorname{\mathtt{override(m, D, C \rightarrow C_{0})}}\) 能判定在类 D 的子类中是否能够重载 \(m: \overline{C} \rightarrow C_{0}\)。这是因为父类的方法在子类中重载时不能改变签名。
Evaluation
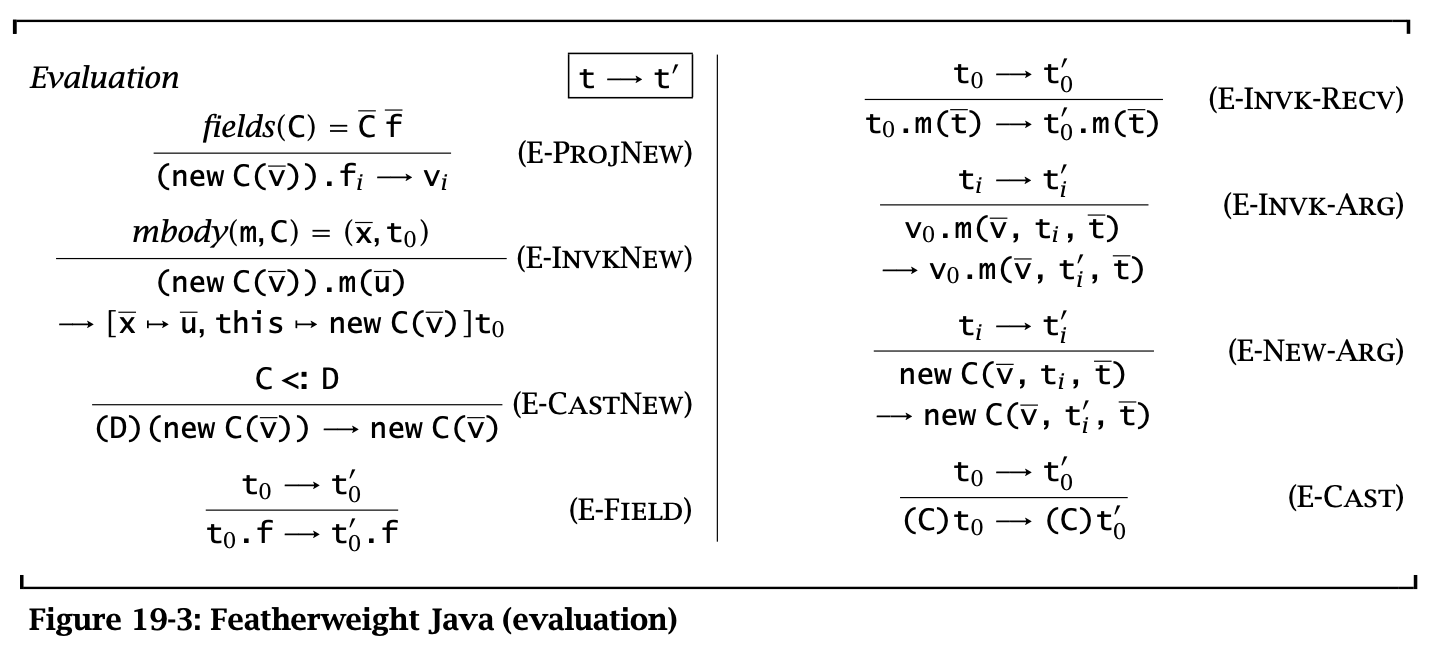
Figure 3: Featherweight Java (Evaluation)
这里的规则都是 call-by-value 的。此处 cast 的运行时行为是检查对象的实际类型是否是转换类型的 subtype。如果是,则转换操作被丢弃并且结果是对象本身。在FJ中,类型转换失败不会引发异常,而是会 stuck。
Typing

Figure 4: Featherweight Java (Typing)
类型转换有三种规则,分别是向上转型,向下转型,以及 FJ 中引入的一个创新:stupid casts。Java 会拒绝 stupid casts,但是在 FJ 中会接受 stupid casts。这是为了 small-step semantics 的 type safety 的 preservation theorem。以下面这个程序为例(其中 A 和 B 没有 subtyping 关系),一个(看起来)不包含 stupid casts 最后可能会 evaluate 到一个包含 stupid cast 的情况:
\[(A)(\operatorname{\mathtt{Object}})\operatorname{\mathtt{new}}\ B() \rightarrow (A)\operatorname{\mathtt{new}}\ B()\]
只有在 type infer 时不包含这条规则时,FJ 的类型才能和 Java 的类型对应。
M OK in C 会检测类 \(C\) 中是否能定义方法 \(M\),读作“Method declaration \(M\) is well formed if it occurs in class \(C\).”;C OK 会检测类 \(C\) 的定义是否合法,即检查构造函数是否对父类的字段使用 super 并初始化本类的字段,以及类中的每个方法声明是否合法,读作“Class declaration \(CL\) is well formed.”。
此处一个 term 的类型可能依赖于它调用的方法的类型,而方法的类型依赖于 term(方法体)的类型,所以这里需要检查是否存在循环;事实上没有,由于每个方法的类型都被明确标注了,因此可以先加载类表并使用它进行类型检查,然后分别检查每个类。
Property
Preservation
If \(\operatorname{\mathtt{mtype}}(m, D) = C \rightarrow C_{0}\), then \(\operatorname{\mathtt{mtype}}(m, C) = C \rightarrow C_0\) for all \(C <: D\).
对 \(C <: D\) 进行归纳即可。注意由于 \(\operatorname{\mathtt{override}}\),因此 \(\operatorname{\mathtt{mtype}}(m, C)\) = \(\operatorname{\mathtt{mtype}}(m, E)\),其中 \(CT( C) = \operatorname{\mathtt{class}}\ C\ \operatorname{\mathtt{extends}}\ E\ \{ \dots \}\)
(Term substitution preserves typing)
If \(\Gamma , \overline{x} : \overline{B} \vdash t : D\) and \(\Gamma \vdash \overline{s} : \overline{A}\), where \(\overline{A} <: \overline{B}\), then \(\Gamma \vdash [\overline{x} \mapsto \overline{s}]t : C\) for some \(C <: D\).
对 \( \Gamma, \overline{x} : \overline{B} \vdash t : D \) 进行归纳:
T-Var:\(t = x\)- 如果 \( x \notin \overline{x} \),则 \( [\overline{x} \mapsto \overline{s}] x = x \) 且 \( \Gamma \vdash x : D \),因此 \( \Gamma \vdash [\overline{x} \mapsto \overline{s}] x : D \)。
- 否则 \( x = x_i \),即 \( Bᵢ = Dᵢ \),则 \( [\overline{x} \mapsto \overline{s}] x = s_i \),即 \( \Gamma \vdash [\overline{x} \mapsto \overline{s}] x: Aᵢ \),又因为 \( Aᵢ <: Bᵢ = Dᵢ \),因此 \( C = Aᵢ <: D \)
T-Field:\( t = t_0.f \quad \Gamma, \overline{x}: \overline{B} \vdash t_0 : D₀ \quad \operatorname{\mathtt{fields}}(D₀) = \overline{C} \overline{f} \quad D = C_i \)根据归纳假设,\( \exist C_0. \Gamma \vdash [\overline{x} \mapsto \overline{s}] t_0 : C_0 \text{ where } C_0 <: D₀ \),而 \( \operatorname{\mathtt{fields}}(C_0) = (\operatorname{\mathtt{fields}}(D₀), \overline{C} \overline{g}) \),因此 \( \Gamma \vdash ([\overline{x} \mapsto \overline{s}]).fᵢ : C_i = D <: D \)
T-Invk:\( t = t_0.m(\overline{t}) \quad \Gamma, \overline{x} : \overline{B} \vdash t_0 : D₀ \quad \operatorname{\mathtt{mtype}}(m, D₀) = \overline{E} \rightarrow D \quad \Gamma, \overline{x} : \overline{B} \vdash \overline{t} : \overline{D} \text{ where } \overline{D} <: \overline{E} \)根据归纳假设,\( \exist C_0. \Gamma \vdash [\overline{x} \mapsto \overline{s}] t_0 : C_0 \text{ where } C_0 <: D₀ \) 且 \( \Gamma \vdash [\overline{x} \mapsto \overline{s}]\overline{t} : \overline{C} \text{ where } \overline{C} <: \overline{D} \),根据上面的 lemma 可知 \(\operatorname{\mathtt{mtype}}(m, C₀) = \overline{E} \rightarrow D\),因此 \( \Gamma \vdash [\overline{x} \mapsto \overline{s}]t : D <: D \)
T-New:\( t = \operatorname{\mathtt{new}}\ C(\overline{t}) \quad \operatorname{\mathtt{fields}}( C) = \overline{D} \overline{f} \quad \Gamma, \overline{x} : \overline{B} \vdash \overline{t} : \overline{C} \text{ where } \overline{C} <: \overline{D} \)根据归纳假设,\( \exist E. \Gamma \vdash [\overline{x} \mapsto \overline{s}]\overline{t} : \overline{E} \text{ where } \overline{E} <: \overline{C} \),由传递性知 \( E <: D \),因此 \( \Gamma \vdash [\overline{x} \mapsto \overline{s}]\operatorname{\mathtt{new}}\ C(\overline{t}) : D <: D \)
T-UCast:\( t = (D)t_0 \quad \Gamma, \overline{x} : \overline{B} \vdash t_0 : C \quad C <: D\)根据归纳假设 \( \exist E. \Gamma \vdash [\overline{x} \mapsto \overline{s}] t_0 : E \text{ where } E <: C \),根据传递性有 \( E <: D \),因此 \( \Gamma \vdash [\overline{x} \mapsto \overline{s}](D)t_0 : D <: D \)
T-DCast:\( t = (D)t_0 \quad \Gamma, \overline{x} : \overline{B} \vdash t_0 : C \quad (D <: C) \quad C \ne D\)根据归纳假设 \( \exist E. \Gamma \vdash [\overline{x} \mapsto \overline{s}] t_0 : E \text{ where } E <: C \)。
- 假设 \( E <: D \) 或者 \( D <: E \),则根据
T-UCast或T-DCast有 \( \Gamma \vdash (D)([\overline{x} \mapsto \overline{s}]t_0) : D \) - 否则使用
T-SCast可以推出
- 假设 \( E <: D \) 或者 \( D <: E \),则根据
T-SCast:\( t = (D)t_0 \quad \Gamma, \overline{x} : \overline{B} \vdash t_0 : C \quad D \not\lt : C \quad C \not\lt : D \)根据归纳假设 \( \exist E. \Gamma \vdash [\overline{x} \mapsto \overline{s}] t_0 : E \text{ where } E <: C \)。假设 \( E <: D \),由于在 FJ 中每个类只有一个父类,那么必然存在 \( C <: D \lor D <: C \),矛盾。所以根据
T-SCast可以推出 \( \Gamma \vdash (D)([\overline{x} \mapsto \overline{s}]t_0) : D \)
(Weakening)
If \(\Gamma \vdash t : C\), then \(\Gamma, x : D \vdash t : C\).
Trivial.
If \(\operatorname{\mathtt{mtype}}(m, C_0) = \overline{D} \rightarrow D\), and \(\operatorname{\mathtt{mbody}}(m, C_0) = (\overline{x}, t)\), then for some \(D_0\) with \( C_0 <: D_0 \) and some \(C <: D\), we have \(\overline{x}: \overline{D}, \operatorname{\mathtt{this}}: D_0 \vdash t: C\).
对 \( \operatorname{\mathtt{mbody}}(m, C_0) \) 进行归纳:
如果 \( m \in CT(C_0) \),由于
m OK in C0,因此有 \( \overline{x} \in \overline{D}, \operatorname{\mathtt{this}}: C_0 \vdash t : E₀ <: D \),其中 \( D_0 = C_0, C = E₀ \)如果 \( m \in CT(C_0’) \text{ where } C_0 = \operatorname{\mathtt{class}}\ C₀\ \operatorname{\mathtt{extends}}\ C₀’\ \{ \dots \} \)
根据归纳假设有 \(\exist D_0 (C_0’ <: D_0). \exist C <: D. \overline{x}: \overline{D}, \operatorname{\mathtt{this}}: D_0 \vdash t: C\)。根据传递性有 \( C_0 <: C_0’ <: D_0 \)
(Preservation)
If \(\Gamma \vdash t : C\) and \(t \rightarrow t’\), then \(\Gamma \vdash t’ : C’\) for some \(C’ <: C\).
对 \( t \rightarrow t’ \) 中使用的最后一条 rule 进行归纳:
E-ProgNew:\( t = \operatorname{\mathtt{new}}\ C_0(\overline{v}).fᵢ \quad t’ = vᵢ \quad \operatorname{\mathtt{fields}}(C_0) = \overline{D} \overline{f} \)根据 \( t \) 的形式可以知道 \( \Gamma \vdash t : C \) 的最后一条规则一定是
T-Field,并且有 \( \exist D₀. \Gamma \vdash \operatorname{\mathtt{new}}\ C_0(\overline{v}) : D_0 \) 以及 \( C = D_i \)。同理 \( \Gamma \vdash \operatorname{\mathtt{new}}\ C_0(\overline{v}) : D₀ \) 的最后一条规则一定是T-New,并且有 \( \exist \overline{C}. \Gamma \vdash \overline{v} : \overline{C} \) 以及 \( \overline{C} <: \overline{D} \)。因此 \( \Gamma \vdash C_i <: D_i \)。E-InvkNew:\( t = \operatorname{\mathtt{new}}\ C_0(\overline{v}).m(\overline{u}) \quad t’ = [\overline{u} \mapsto \overline{x}, \operatorname{\mathtt{new}}\ C_0(\overline{v}) \mapsto \operatorname{\mathtt{this}}]t_0 \quad \operatorname{\mathtt{mbody}}(m, C_0) = (\overline{x}, t_0)\)同理,根据 \( t \) 的形式可以知道 \( \Gamma \vdash t : C \) 的最后两条规则一定是
T-Invk和T-New,并且有\[ \Gamma \vdash \operatorname{\mathtt{new}}\ C_0(\overline{v}): C_0 \quad \Gamma \vdash \overline{u} : \overline{C} \quad \overline{C} <: \overline{D} \quad \operatorname{\mathtt{mtype}}(m, C_0) = \overline{D} \rightarrow C \]
根据前面的 lemma 有 \( \exist D₀ (C_0 <: D_0). \exist B (B <: C). \overline{x} : \overline{D}, \operatorname{\mathtt{this}} : D_0 \vdash t_0 : B \)
根据 Weakening lemma 有 \( \Gamma, \overline{x}: \overline{D}, \operatorname{\mathtt{this}} : D₀ \vdash t_0 : B \)
根据 Term substitution preserves typing lemma 有 \( \exist E. \Gamma \vdash [\overline{x} \mapsto \overline{u}, \operatorname{\mathtt{this}} \mapsto \operatorname{\mathtt{new}}\ C_0(\overline{v})]t_0 : E \)
根据传递性有 \( E <: C \),令 \( C’ = E \) 即可。
E-CastNew:\( t = (D)(\operatorname{\mathtt{new}}\ C_0(\overline{v})) \quad C₀ <: D \quad t’ = \operatorname{\mathtt{new}}\ C₀(\overline{v}\)由于 \( C_0 <: D \),所以 \( \Gamma \vdash (D) (\operatorname{\mathtt{new}}\ C_0(\overline{v})): C \) 所使用的最后一条规则一定是
T-UCast。因此可以得到 \( \Gamma \vdash \operatorname{\mathtt{new}}\ C_0(\overline{v}) : C_0 \) 并且 \( D = C \)。E-Invk-Recv/E-Invk-Arg/E-New-Arg/E-Cast的证明步骤比较相似,这里只展示E-Cast的证明过程:\[ t = (D) t_0 \quad t’ = (D) t_0’ \quad t_0 \rightarrow t_0' \]
考虑 \(t\) 所使用的最后一条 typing 规则,有三种情况:
T-UCast:\(\Gamma \vdash t_0 : C_0 \quad C_0 <: D \quad D = C\)根据归纳假设,有 \( \Gamma \vdash t_0’ : C_0’ \) 且 \( C_0’ <: C_0 \)。根据传递性有 \( C_0’ <: C\)。根据
T-UCast成立。T-DCast:\(\Gamma \vdash t_0 : C_0 \quad D <: C_0 \quad D = C\)根据归纳假设,有 \( \Gamma \vdash t_0’ : C_0’ \) 且 \( C_0’ <: C_0 \)。
如果 \( C_0’ <: C \) 或者 \( C <: C_0’ \),那么可以直接使用
T-UCast或T-DCast得到 \( \Gamma \vdash ( C)t_0’ : C \);否则如果 \( C_0’ \not\lt : C \) 且 \( C \not\lt : C_0’ \),那么需要用T-SCast得到 \( \Gamma \vdash ( C)t_0’ : C \)。T-SCast:\(\Gamma \vdash t_0 : C_0 \quad D \not\lt : C_0 \quad C_0 \not\lt : D \quad D = C\)根据归纳假设,有 \( \Gamma \vdash t_0’ : C_0’ \) 且 \( C_0’ <: C_0 \)。因此 \( C_0’ \not\lt : D \) 且 \( D \not\lt : C_0’ \)。因此可以使用
T-SCast得到 \( \Gamma \vdash ( C)t_0’ : C \)。
Progress
在 FJ 中,我们无法实际证明 progress,因为一个 well-typed term 可能会 stuck,因此我们只能证明一个更弱的性质:要么能够 evaluate 到一个值,要么因为 stupid cast 而 stuck。
Suppose \(t\) is a well-typed term.
- If \(t = \operatorname{\mathtt{new}}\ C₀(\overline{t}).f\), then \(\operatorname{\mathtt{fields}}(C_0) = \overline{C}\overline{f}\) and \(f \operatorname{\mathtt{in}} \overline{f}\)
- If \(t = \operatorname{\mathtt{new}}\ C₀(\overline{t}).m(\overline{s})\), then \(\operatorname{\mathtt{mbody}}(m, C_0) = (\overline{x}, t_0)\) and \(\vert \overline{x} \vert = \vert \overline{s} \vert\)
The set of evaluation contexts for FJ is defined as follows:
\begin{aligned} E \Coloneqq & & (\text{eval contexts}) \\ & [] & (\text{hole}) \\ & E.f & (\text{field access}) \\ & E.m(\overline{t}) & (\text{method invocation} (receiver)) \\ & v.m(\overline{v}, E, \overline{t}) & (\text{method invocation} (arg)) \\ & \operatorname{\mathtt{new}}\ C(\overline{v}, E, \overline{t}) & (\text{object creation (arg)}) \\ & ( C)E\ t & (\text{cast}) \\ \end{aligned}
每个 evaluation context 都是一个带 hole 的 term,其中 \(E[t]\) 则表示将 hole 替换为 \(t\)。这里的 hole 表示下一个被规约的 sub-term:设在 \(t \rightarrow t’\) 的过程中使用 \(r \rightarrow r’\),即 \(t = E[r], t’ = E[r’]\)。
(Progress)
Suppose \(t\) is a closed, well-typed normal form. Then either:
- t is a value, or
- for some evaluation context \(E\), we can express \(t\) as \(t = E[( C)(\operatorname{\mathtt{new}}\ D(v))]\), with \(D \not\lt: C\).
对类型推导进行归纳即可。
第二种情况对应着 stupid cast,即 stuck 的情况。
此处进展性质可以更强:如果 \(t\) 仅包含上转型,那么它不会 stuck。
Encodings vs. Primitive Objects
上一章利用语法糖的形式编码了 OOP,这一章则将其看作 primitives 来实现。
编码的方式揭示了封装和重用的基本机制,便于与其他机制进行比较,并展示了对象如何被编译器翻译成更低级的语言。此外,它还展示了对象与其他语言特性的交互。
原生的方式能够直接讨论对象的操作语义和类型行为,更适合用于高级语言的设计和文档撰写。
一般来说在研究语言时会结合两种方式:一方面是包含对象、类等原始特性的高级语言,具有自己的类型规则和操作语义;另一方面是将这种语言翻译成低级语言,并证明这种翻译正确地实现了高级语言的求值和类型属性。