前面使用的 subtyping rules 并不适合实际实现,因为它们并不是自底向上构建的,主要问题在于下面两个规则:
T-Sub\[\dfrac{\Gamma \vdash t : S \quad S <: T}{\Gamma \vdash t : T} \tag{T-Sub}\]
其他大部分 typing rules 都是对于某个特殊结构进行类型推导(syntax-directed),而
T-Sub的推导对象是一个 metavar \(t\),因此这条规则总可以对一个 term 使用,且目标类型 \(T\) 是未知的,需要程序来决定使用的时机。S-Trans\[\dfrac{S <: U \quad U <: T}{S <: T} \tag{S-Trans}\]
S-Trans也有类似的问题。并且除此之外,S-Trans在使用时需要程序自己推理出一个中间变量 \(U\),这对程序来说是很困难的。S-Refl\[S <: S \tag{S-Refl}\]
S-Refl中没有假设条件,因此这一条也是在任何时候都可以使用的,它也不是 syntax-directed 的。
因此本章使用新的 typing rules 替代原有的规则(称为 declarative relation),称为 algorithmic subtyping 和 algorithmic typing,其推断过程是 syntax-directed 的。然后会证明这些规则和原有规则是等价的(即可以互相推导)。
Algorithmic Subtyping
本章将介绍一个算法,用于判断一个类型是否是另一个类型的 subtype。这个算法是 syntax-directed 的,即对于每个类型都有一个对应的规则。
Definition and equivalence
Typechecker 在判断 \(S <: T\) 时会判断 \((S, T)\) 是否包含在 \(\mapsto S <: T\)(称为 \(S\) is algorithmically a subtype of \(T\),并且是 syntax-directed 的) 中。Algorithmic subtyping relation 里中去掉了 S-Trans 和 S-Refl 这两条规则,并让这两条规则直接蕴含在其他具体的规则中。
首先,对于之前 record types 定义了三条规则,分别是 S-RcdDepth,S-RcdWidth 和 S-RcdPerm。这三条规则在使用时往往需要配合 S-Trans 使用,因此这里将这三条规则合并为 S-Rcd。
\[\dfrac{\{l_{i}^{i \in 1 \dots n}\} \subseteq \{k_{j}^{j \in 1 \dots m}\} \quad k_j = l_i \rightarrow S_j <: T_i}{\{k_{j} : S_j^{j \in 1 \dots m}\} <: \{l_{i} : T_i^{i \in 1 \dots n}\} } \tag{S-Rcd}\]
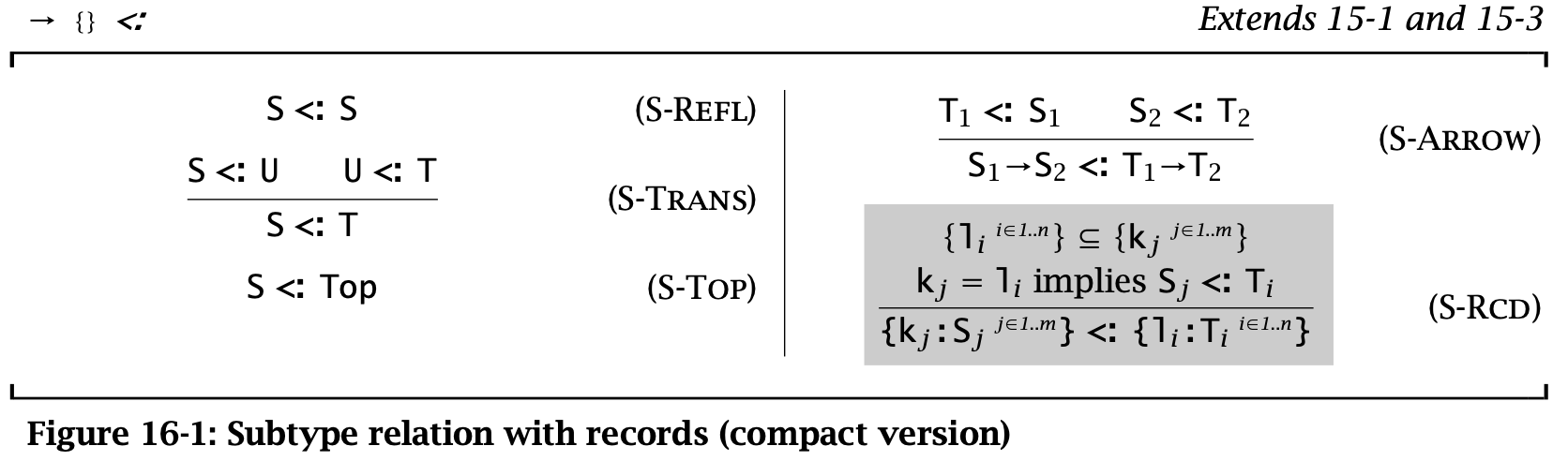
Figure 1: Subtype relation with records
If \(S <: T\) is derivable from the subtyping rules including S-RcdDepth, S-RcdWidth, and S-RcdPerm (but not S-Rcd), then it can also be derived using S-Rcd (and not S-RcdDepth, S-Rcd-Width, or S-Rcd-Perm), and vice versa.
下面证明 S-Refl 和 S-Trans 在上面的规则中(即仅包含函数和 record type 的 subtyping 系统)都是不必要的。
- \(S <: S\) can be derived for every type \(S\) without using
S-Refl. - If \(S <: T\) is derivable, then it can be derived without using
S-Trans.
只要证明 S-Refl 和 S-Trans 都可以用其他规则表示。
第一个 lemma 直接对 \(S\) 的推导进行归纳。对于不同的类型使用的 S-Refl 分别使用 S-Top,S-Arrow 和 S-Rcd 替代。如果增加了更多的 base type,则需要分别加入对应的 S-Base(例如 Bool <: Bool)。
下面主要证明第二个 lemma。由于 S-Trans 的假设都是 subtyping 规则,因此只需要考虑 S-*。对 derivations 的大小进行归纳,假设比当前小的都成立。如果 derivations 中应用的最后一条规则不是 S-Trans,那么根据归纳假设,前面的部分也可以不用 S-Trans,成立。
因此下面考虑最后一条规则是 S-Trans 的情况——即存在两个 sub-derivations \(S <: U\) 和 \(U <: T\),并且两个 subderivations 中都没有用到 S-Trans。讨论两个 sub-derivations 的最后一条规则:
Any +
S-Top:直接替换成S-TopS-Top+ Any:则U = Top,则T也是Top,那么右侧一定是S-Top,归于第一条S-Arrow+S-Arrow:\begin{aligned} & S = S_1 \rightarrow S_2 \\ & U = U_1 \rightarrow U_2 \\ & T = T_1 \rightarrow T_2 \end{aligned}
\begin{aligned} & U_1 <:S_1 & S_2 <:U_2 \\ & T_1 <:U_1 & U_2 <:T_2 \end{aligned}
即
\[ \dfrac{ \dfrac{\dfrac{…}{U_1 <:S_1} \quad \dfrac{…}{S_2 <:U_2}}{S <: U} (\operatorname{\mathrm{S-Arrow}}) \quad \dfrac{\dfrac{…}{T_1 <:U_1} \quad \dfrac{…}{U_2 <:T_2}}{U <: T}(\operatorname{\mathrm{S-Arrow}}) } {S <: T} (\operatorname{\mathrm{S-Trans}}) \]
这一段可以替换为等价的:
\[ \dfrac{ \dfrac{ \dfrac{…}{U_1 <: S_1} \quad \dfrac{…}{T_1 <:U_1} }{T_1 <: S_1} (\operatorname{\mathrm{S-Trans}}) \quad \dfrac{\dfrac{…}{S_2 <:U_2} \quad \dfrac{…}{U_2 <:T_2}}{S_2 <: T_2}(\operatorname{\mathrm{S-Trans}}) } {S <: T} (\operatorname{\mathrm{S-Arrow}}) \]
根据归纳假设,两个 sub-derivations 也可以被改写为完全不需要
S-Trans的形式。因此在整个证明中可以完全不用到S-Trans,证毕。S-Rcd+S-Rcd:类似S-Arrow/S-ArrowS-Arrow+S-Rcd和S-Rcd/S-Arrow:不可能
证明 S-Trans 是不必要的这个过程称为 transitivity elimination,是 cut elimination 的一个特例。
(algorithmic subtyping relation)
The algorithmic subtyping relation is the least relation on types closed under the rules in the figure below.
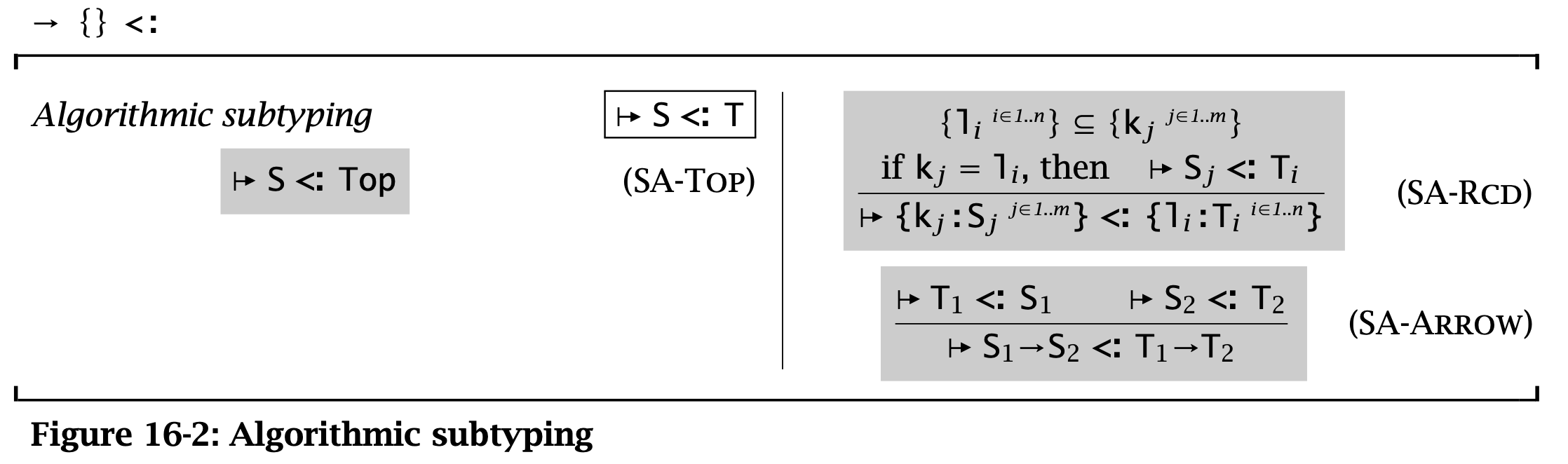
Figure 2: Algorithmic subtyping
Algorithmic subtyping relation 和原先的 subtyping relation 是等价的:
(Soundness and completeness)
\(S <: T \iff \mapsto S <: T\)
根据上面的两个引理通过归纳易证。
Implementation
根据上面的规则,可以实现一个算法来判断 \(S <: T\) 是否成立。这个算法是 syntax-directed 的:
\begin{algorithm} \caption{Algorithmic Subtyping} \begin{algorithmic} \procedure{subtype}{$S, T$} \if{$T = \operatorname{\mathtt{Top}}$} \return{true} \elseif{$S = S_1 \rightarrow S_2 \land T = T_1 \rightarrow T_2$} \return{subtype($T_1, S_1$) $\land$ subtype($S_2, T_2$)} \elseif{$S = \{k_j : S_j^{j \in 1 \dots m}\} \land T = \{l_i : T_i^{i \in 1 \dots n}\}$} \return{$\{l_i^{i \in 1 \dots n}\} \subseteq \{k_j^{j \in 1 \dots m}\} \land (\forall i, \exists j, k_j = l_i$ $\land$ subtype($S_j, T_i$))} \else \return{false} \endif \endprocedure \end{algorithmic} \end{algorithm}
Termination
(Termination)
If \(\mapsto S <: T\) is derivable, then \(\operatorname{\mathtt{subtype}}(S, T)\) will return true.
If not, then subtype(S, T) will return false.
因为算法是 syntax-directed 的,对 type derivations 的过程进行归纳即可就能证明正确细节。
下面只要证明算法会终止。观察算法可以发现,每次进行递归时,类型的 size 都会单调减小,因此算法一定会终止。
Soundness, completeness and termination 共同保证了这个算法是 decidable 的。采用 algorithmic definition 作为定义虽然看似节省时间,但实际上不适合进行证明,因此这里优先叙述 declarative definition。
Algorithmic Typing
Definition
在 algorithmic subtyping 中,我们去掉了 S-Trans 和 S-Refl,并且证明了这两条规则是不必要的。在本章中,我们会继续去掉 T-Sub。
考虑在类型推导中使用 T-Sub 的场景,下面首先证明一个 lemma:当类型推导中使用了 T-Sub 时,总可以将用到它的推导“下移”。
考虑在 derivations 中 T-Sub 后紧跟的规则(T-Var 可以被直接排除):
T-Abs\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma, x:S_1 \vdash s_2 : S_2} \quad \dfrac{…}{S_2 <: T_2} }{\Gamma, x:S_1 \vdash s_2 : T_2} (\operatorname{\mathrm{T-Sub}}) } {\Gamma \vdash \lambda x:S_1 . s_2 : S_1 \rightarrow T_2}(\operatorname{\mathrm{T-Abs}}) \]
由于最后一条规则是
T-Abs,那么T-Sub一定是对函数类型的部件(参数类型或返回类型)使用。而这种情况可以直接使用S-Arrow拼凑出 subtyping 关系,然后再使用T-Sub。\[\dfrac{ \dfrac{ \dfrac{…}{\Gamma, x:S_1 \vdash s_2 : S_2} }{\Gamma \vdash \lambda x:S_1 . s_2 : S_1 \to S_2} (\operatorname{\mathrm{T-Abs}}) \quad \dfrac{ \dfrac{…}{S_1 <: S_1}(\operatorname{\mathrm{S-Refl}}) \quad \dfrac{…}{S_2 <: T_2} }{S_1 \to S_2 <: S_1 \to T_2} (\operatorname{\mathrm{S-Arrow}}) } {\Gamma \vdash \lambda x:S_1 . s_2 : S_1 \to T_2} \]
T-App在
T-App前使用T-Sub有两种可能的情况:对函数使用T-Sub或者对参数使用T-Sub。对函数使用
T-Sub\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash s_{1} : S_{11} \rightarrow S_{12}} \quad \dfrac{…}{S_{11} \rightarrow S_{12} <: T_{11} \rightarrow T_{12}} (\operatorname{\mathrm{S-Arrow}}) }{ \Gamma \vdash s_1 : T_{11} \rightarrow T_{12} } (\operatorname{\mathrm{T-Sub}}) \quad \dfrac{…}{\Gamma \vdash s_{2} : T_{11}} }{ \Gamma \vdash s_{1}\ s_{2} : T_{12} } (\operatorname{\mathrm{T-APP}}) \]
这里值得注意的是使用了
S-Arrow的这个 sub-derivations,根据上一节的讨论可以知道在 derivations 中总可以将S-Refl和S-Trans去掉,因此这里假设直接使用了S-Arrow:\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash s_{1} : S_{11} \rightarrow S_{12}} \quad \dfrac{ \dfrac{…}{T_{11} <: S_{11}} \quad \dfrac{…}{S_{12} <: T_{12}} }{S_{11} \rightarrow S_{12} <: T_{11} \rightarrow T_{12}} (\operatorname{\mathrm{S-Arrow}}) }{ \Gamma \vdash s_1 : T_{11} \rightarrow T_{12} } (\operatorname{\mathrm{T-Sub}}) \quad \dfrac{…}{\Gamma \vdash s_{2} : T_{11}} }{ \Gamma \vdash s_{1}\ s_{2} : T_{12} } (\operatorname{\mathrm{T-APP}}) \]
当对函数的结果类型使用
T-Sub时,可以先使用T-App再使用T-Sub;对函数的参数类型使用T-Sub时,可以将其变成对T-App的参数使用T-Sub,但是注意到这时会多出一个T-Sub,仍然处于T-App的上方。实际上被挪下来的T-Sub只是对结果类型使用的规则,对参数类型使用的T-Sub无法被挪下来。\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash s_1 : S_{11} \rightarrow S_{12}} \quad \dfrac{ \dfrac{…}{\Gamma \vdash s_2 : T_{11}} \quad \dfrac{…}{T_{11} <: S_{11}} }{\Gamma \vdash s_{2} : S_{11}} (\operatorname{\mathrm{T-Sub}}) }{\Gamma \vdash s_{1}\ s_{2} : T_{11}} (\operatorname{\mathrm{T-App}}) \quad \dfrac{…}{\Gamma \vdash s_2 : T_{11}} } {\Gamma \vdash s_1\ s_2 : T_{12}} (\operatorname{\mathrm{T-Sub}}) \]
对参数使用
T-Sub\[ \dfrac{ \dfrac{ … }{\Gamma \vdash s_1 : T_{11} \rightarrow T_{12}} \quad \dfrac{ \dfrac{ … }{\Gamma \vdash s_2 : T_2} \quad \dfrac{ … }{T_2 <: T_{11}} }{\Gamma \vdash s_2 : T_{11}} \ (\operatorname{\mathrm{T-Sub}}) } {\Gamma \vdash s_1\ s_2 : T_{12}} \ (\operatorname{\mathrm{T-App}}) \]
类似前面的结论,这里的
T-Sub不能被挪下来:\[ \dfrac{ \dfrac{ \dfrac{ … }{\Gamma \vdash s_1 : T_{11} \rightarrow T_{12}} \quad \dfrac{ \dfrac{ … }{T_2 <: T_{11}} \quad \dfrac{ … }{T_{12} <: T_{12}} (\operatorname{\mathrm{S-Refl}}) }{T_{11} \rightarrow T_{12} <: T_2 \rightarrow T_{12}} (\operatorname{\mathrm{S-Arrow}}) } {\Gamma \vdash s_1 : T_2 \rightarrow T_{12}} (\operatorname{\mathrm{T-Sub}}) \quad \dfrac{ … }{\Gamma \vdash s_2 : T_2} }{\Gamma \vdash s_1\ s_2 : T_{12}} (\operatorname{\mathrm{T-App}}) \]
T-Sub\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash s : S} \quad \dfrac{…}{S <: U} }{\Gamma \vdash s : U} (\operatorname{\mathrm{T-Sub}}) \quad \dfrac{…}{U <: T} } {\Gamma \vdash s : T} (\operatorname{\mathrm{T-Sub}}) \]
连续的
T-Sub可以用S-Trans进行合并;并且根据前面的讨论,S-Trans也可以被消去。\[ \dfrac{ \dfrac{…}{\Gamma \vdash s : S} \quad \dfrac{ \dfrac{…}{S <: U} \quad \dfrac{…}{U <: T} }{\Gamma \vdash s : T} (\operatorname{\mathrm{S-Trans}}) } {\Gamma \vdash s : T} (\operatorname{\mathrm{T-Sub}}) \]
T-Rcd\[ \dfrac{ \dfrac{…}{\Gamma \vdash t_{i} : T_{i}^{i \in 1 \dots k-1, k+1 \dots n}} \quad \dfrac{ \dfrac{…}{\Gamma \vdash t_{k} : S} \quad \dfrac{…}{S <: T_{k}} }{\Gamma \vdash t_{k} : T_{k}} (\operatorname{\mathrm{T-Sub}}) }{ \Gamma \vdash \{l_{i} = t_{i}^{i \in 1 \dots n}\} : \{l_{i} : T_{i}^{i \in 1 \dots n}\} } \operatorname{\mathrm{(T-Rcd)}} \]
利用
S-Rcd,这里的T-Sub可以被挪下来:为了方便,这里记 \(\mathcal{T}_k = 1 \dots k-1, k+1 \dots n\)
\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash t_{i} : T_{i}^{i \in \mathcal{T}_k}} \quad \dfrac{…}{\Gamma \vdash t_{k} : S} }{ \Gamma \vdash \{l_{i} = t_{i}^{i \in 1 \dots n}\} : \{l_{i} <: T_{i}^{i \in \mathcal{T}_k}, l_k <: S\} } \operatorname{\mathrm{(T-Rcd)}} \quad \dfrac{ \dfrac{…}{S <: T_{k}} \quad \dfrac{}{T_{i}^{i \in \mathcal{T}_k} <: T_{i}^{i \in \mathcal{T}_k}} (\operatorname{\mathrm{S-Refl}}) }{ \Gamma \vdash \{l_{j} : T_j^{j \in \mathcal{T}_k}, l_{k} : S\} <: \{l_{i} : T_i^{i \in 1 \dots n}\} } \operatorname{\mathrm{(S-Rcd)}} }{ \Gamma \vdash \{l_{i} = t_{i}^{i \in 1 \dots n}\} : \{l_{i} : T_{i}^{i \in 1 \dots n}\} } \operatorname{\mathrm{(S-Sub)}} \]
T-Proj\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash t_{} : \{l_i : S_i^{1 \dots n}\}} \quad \dfrac{…}{\{l_i : S_i^{1 \dots n}\} <: \{l_i : T_i^{1 \dots n}\}} }{\Gamma \vdash t_{} : \{l_i : T_i^{1 \dots n}\}} (\operatorname{\mathrm{T-Sub}}) }{ \Gamma \vdash t.l_j : T_j } \operatorname{\mathrm{(T-Proj)}} \]
类似的,这里的
T-Sub也可以被挪下来:\[ \dfrac{ \dfrac{ \dfrac{…}{\Gamma \vdash t_{} : \{l_i : S_i^{1 \dots n}\}} }{\Gamma \vdash t.l_j : S_j} \operatorname{\mathrm{(T-Proj)}} \quad \dfrac{…}{\{l_i : S_i^{1 \dots n}\} <: \{l_i : T_i^{1 \dots n}\}} }{ \Gamma \vdash T.l_j : T_j } (\operatorname{\mathrm{T-Sub}}) \]
综合上面的讨论,可以发现经过变换后,T-Sub 只会出现在两个位置上:
对 application 的参数使用(即
t1 t2中对t2使用),使其与 abstraction 的参数类型相匹配:为了解决这个问题,我们可以将T-App替换成一个包含T-Sub的更强的版本:\[\dfrac{\Gamma \vdash t_{1} : T_{11} \rightarrow T_{12} \quad \Gamma \vdash t_2 : T_2 \quad T_2 <: T_{11}} {\Gamma \vdash t_1\ t_2 : T_{12}}\]
这条规则是 syntax-directed 的。
对 type derivations 最后的结果使用:这种情况发生在 derivations 的末尾,因此不影响中间的类型推导,只是最后的类型会更“小”
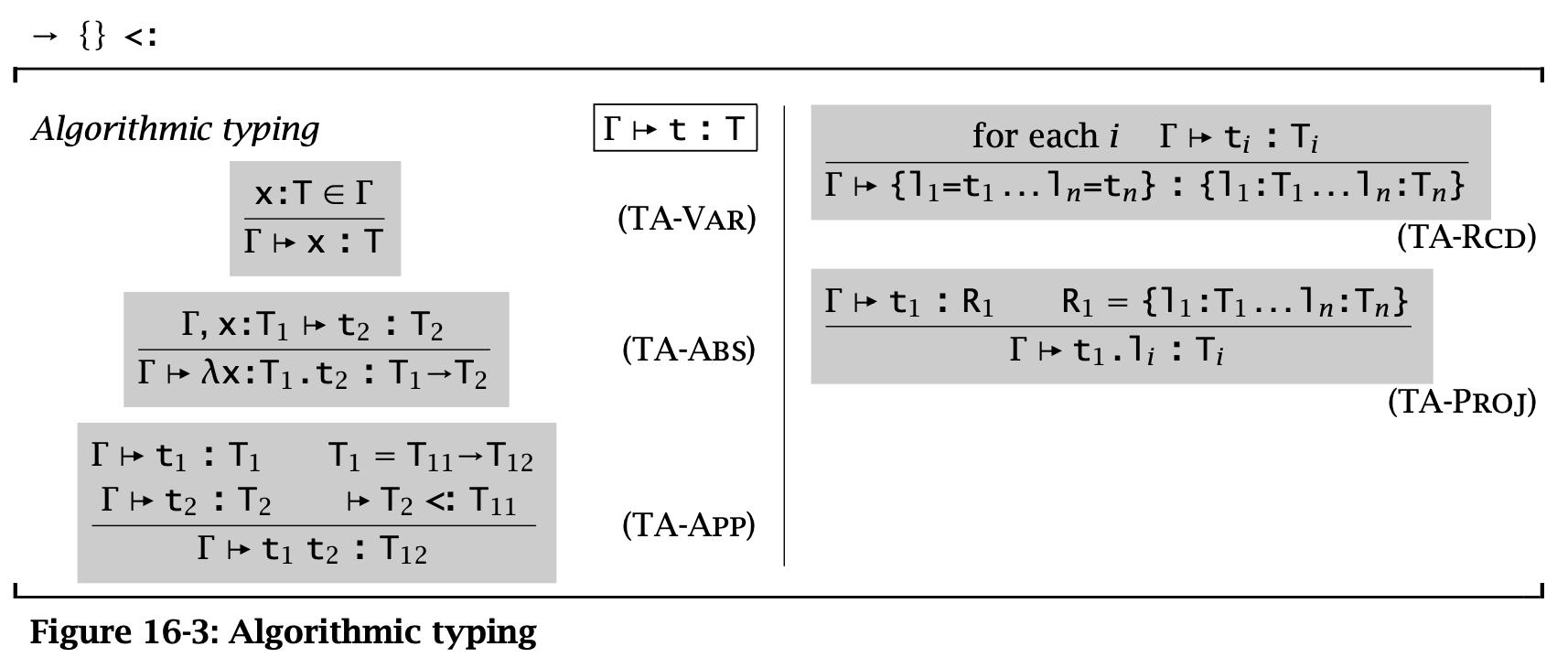
Figure 3: Algorithmic typing
(The algorithmic typing relation)
The algorithmic typing relation is the least relation closed under the rules in the figure.
Soundness and completeness
(Soundness)
If \(\Gamma \mapsto t : T\), then \(\Gamma \vdash t : T\).
根据 type derivations 进行归纳即可。Algorithmic typing relation 的推导规则和 declarative typing relation 几乎完全相同,唯一的区别在于 TA-App,它等价于先用 T-Sub 再用 T-App。
(Completeness / Minimal Typing)
If \(\Gamma \vdash t : T\), then \(\Gamma \mapsto t : S\) for some \(S <: T\).
根据 declarative type derivations 进行归纳,考虑根据 derivations 中最后一条规则。这里需要注意的是在 algorithmic typing relation 中,推导的结果可能是实际结果的 subtype,即可能会更“小”,因此需要证明这个:
T-Var:立即由 TA-Var 得出。T-Abs:\begin{aligned} & t = \lambda x:T_1. t_2 \\ & \Gamma, x:T_1 \vdash t_2 : T_2 \\ & T = T_1 \rightarrow T_2 \end{aligned}
根据归纳假设,存在某个 \(S_2 <: T_2\) 使得 \(\Gamma, x:T_1 \mapsto t_2 : S_2\)。由
TA-Abs有,\(\Gamma \mapsto t : T_1 \rightarrow S_2\)。由
S-Arrow,\(T_1 \rightarrow S_2 <: T_1 \rightarrow T_2\),成立。T-App:如果 \(t = t_1\ t_2\),且 \(\Gamma \vdash t_1 : T_{11} \rightarrow T_{12}\) 和 \(\Gamma \vdash t_2 : T_{11}\),其中 \(T = T_{12}\)。根据归纳假设,存在某个 \(S_1 <: T_{11} \rightarrow T_{12}\) 使得 \(\Gamma \vdash^n t_1 : S_1\),且存在某个 \(S_2 <: T_{11}\) 使得 \(\Gamma \vdash^n t_2 : S_2\)。根据子类型关系的反演引理(15.3.2),\(S_1\) 必须有形式 \(S_{11} \rightarrow S_{12}\),对于某些 \(S_{11}\) 和 \(S_{12}\) 有 \(T_{11} <: S_{11}\) 且 \(S_{12} <: T_{12}\)。通过传递性,\(S_2 <: S_{11}\)。根据算法子类型的完备性(16.2.6 16.3.2),\(\vdash^n S_2 <: S_{11}\)。现在,由 TA-App,\(\Gamma \vdash^n t_1 t_2 : S_{12}\),完成此情况(因为我们已经有 \(S_{12} <: T_{12}\))。T-Rcd:如果 \(t = \{l_i=t_i\ i\in1..n\}\),且 \(\Gamma \vdash t_i : T_i\) 对每个 \(i\),其中 \(T = \{l_i:T_i\ i\in1..n\}\)。直接得出。T-Proj:如果 \(t = t_1.l_j\),且 \(\Gamma \vdash t_1 : \{l_i:T_i\ i\in1..n\}\),其中 \(T = T_j\)。类似于应用情况。T-Sub:如果 \(t : S\) 且 \(S <: T\),直接得出。
Joins and Meets
在一个控制流分支中,多个分支可能返回不同的类型。
\[ \operatorname{\mathtt{if}}\ \operatorname{\mathtt{true}}\ \operatorname{\mathtt{then}}\ \{x=\operatorname{\mathtt{true}},y=\operatorname{\mathtt{false}}\}\ \operatorname{\mathtt{else}}\ \{x=\operatorname{\mathtt{false}},z=\operatorname{\mathtt{true}}\} \]
在没有 subtyping 的时候这个表达式不能通过类型检查,但是在 declarative subtyping 下这个表达式的返回值可以是 \(\{x=\operatorname{bool}\}\) 或者 \(\{\}\),而在 algorithmic subtyping 下应当取这些类型的 minimal type,也就是最小公共父类型(least common supertype)。此时称得到的类型是这几个 branches 的 join。
(join)
A type \(J\) is called join of a pair of types \(S\) and \(T\), written \(J = S \vee T\), if \(S <: J\) and \(T <: J\), and for all types \(U\), if \(S <: U\) and \(T <: U\), then \(J <: U\).
(meet)
A type \(M\) is called meet of a pair of types \(S\) and \(T\), written \(M = S \wedge T\), if \(M <: S\) and \(M <: T\), and for all types \(L\), if \(L <: S\) and \(L <: T\), then \(L <: M\).
对于一个 subtyping 关系,如果对于每个类型 \(S\) 和 \(T\) 都有 joins,则这个 subtyping 关系有 joins。类似地,如果对于每个类型 \(S\) 和 \(T\) 都有 meets,则这个 subtyping 关系有 meets。由于这里讨论的 subtyping 只有 \(\operatorname{\mathtt{Top}}\) 而没有 \(\operatorname{\mathtt{Bot}}\),因此只存在 joins 而没有 meets。
Joins 和 meets 的性质有一个弱化版本:如果一对类型 \(S\) 和 \(S\) 存在某个类型 \(L\) 使得 \(L <: S\) 且 \(L <: T\),那么这对类型 \(S\) 和 \(T\) 有下界(bounded below)。对于每一对有下界的类型 \(S\) 和 \(T\),如果存在某个 \(M\) 是 \(S\) 和 \(T\) 的下界,则该 subtyping 关系被认为具有有界下界(bounded below meets)。
Joins 和 meets 不是唯一的,例如 \(\{x: \operatorname{\mathtt{Top}}, y: \operatorname{\mathtt{Top}}\}\) 和 \(\{y: \operatorname{\mathtt{Top}}, x: \operatorname{\mathtt{Top}}\}\) 可以同时是某个类型的 joins。但是某对类型的 joins 和 meets 假设有多个,那么它们之间一定互为 subtyping 关系。
利用 joins 和 meets 可以定义出 \(\operatorname{\mathtt{if}}\) 的 typing rule:
\[ \dfrac{\Gamma \vdash t_1 : T_1 \quad T_1 = \operatorname{\mathtt{Bool}} \qquad \Gamma \vdash t_2 : T_2 \quad \Gamma \vdash t_3 : T_3 \quad T_2 \vee T_3 = T }{\Gamma \vdash \operatorname{\mathtt{if}}\ t_1\ \operatorname{\mathtt{then}}\ t_2\ \operatorname{\mathtt{else}}\ t_3 : T} \tag{TA-If} \]
但是 joins 和 meets 也有可能让类型推导变得更奇怪:例如表达式 \(\operatorname{if}\ \operatorname{true}\ \operatorname{then}\ \operatorname{true}\ \operatorname{else}\ \{\}\) 的类型为 \(\operatorname{\mathtt{Top}}\),这通常不是程序员想要的。通常情况下应当排除掉 joins 为 \(\operatorname{\mathtt{Top}}\) 的情况或者直接发出警告。
Existence of joins and bounded meets
(Existence of joins and bounded meets)
- For every pair of types \(S\) and \(T\), there is some type \(J\) such that \(S \vee T = J\).
- For every pair of types \(S\) and \(T\) with a common subtype, there is some type \(M\) such that \(S \wedge T = M\).
首先给出下面的计算 joins 和 meets 的算法:
\[ S \vee T = \begin{cases} \operatorname{\mathtt{Bool}} & \text{if $S = T = \operatorname{\mathtt{Bool}}$} \\ M_1 \to J_2 & \text{if $S = S_1 \to S_2,\ T = T_1 \to T_2$} \\ & \quad \text{where $S_1 \land T_1 = M_1;\ S_2 \lor T_2 = J_2$} \\ \{j_l : J_l^{l \in 1 \dots q} \} & \text{if $S = \{k_j : S_j^{j \in 1 \dots m}\},\ T = \{l_i : T_i^{i \in 1 \dots n}\}$} \\ & \quad \text{where $\{j_l^{l \in 1 \dots q}\} = \{k_j^{j \in 1 \dots m}\} \cap \{l_i^{i \in 1 \dots n}\};\ ∀ jₗ = k_j = l_i. S_j \lor T_i = J_l$} \\ \operatorname{\mathtt{Top}} & \text{otherwise} \end{cases} \]
\[ S \wedge T = \begin{cases} S & \text{if $T = \operatorname{\mathtt{Top}}$} \\ T & \text{if $S = \operatorname{\mathtt{Top}}$} \\ \operatorname{\mathrm{Bool}} & \text{if $S = T = \operatorname{\mathrm{Bool}}$} \\ J_1 \to M_2 & \text{if $S = S_1 \to S_2,\ T = T_1 \to T_2$} \\ & \quad \text{where $S_1 \lor T_1 = J_1;\ S_2 \land T_2 = M_2$} \\ \{ m_l : M_l \}_{l \in 1..q} & \text{if $S = \{ k_j : S_j^{j \in 1..m} \},\ T = \{ l_i : T_i^{i \in 1..n}\}$} \\ & \quad \text{where $\{ m_l^{l \in 1..q} \} = \{ k_j^{j \in 1..m} \} \cup \{ l_i^{i \in 1..n} \};\ ∀ m_l = k_j = l_i. S_j \land T_i = M_l$;} \\ & \quad \text{$M_l = Sⱼ\ (m_l = k_j \in S - T)$; $M_l = T_i\ (m_l = l_i \in T - S)$} \\ \operatorname{\mathrm{fail}} & \text{otherwise} \end{cases} \]
这两个算法会相互递归调用(例如计算 \(S \vee T\) 的第二个分支上,即函数类型上时,需要计算 \(S \wedge T\))。此处计算 \(S \wedge T\) 可能会出现 fail 的情况,表明两个类型没有 meets。此时会直接跳到 \(\operatorname{\mathtt{Top}}\) 的情况。
在上面的算法中每一个步骤 \(S\) 和 \(T\) 的 size 都会减小,所以算法一定能够终止,因此 \(\vee\) 和 \(\wedge\) 都是 total functions。
因此 joins 一定存在,但是 meets 可能会有 fail 的情况,下面需要证明如果两个类型有下界,则它们一定有 meets。
If \(L <: S\) and \(L <: T\), then \(S \wedge T = M\) for some \(M\).
首先根据 inversion lemma,如果存在 \(L\) 满足条件,那么 \(S\) 和 \(T\) 的形状必定相同。下面根据 size 进行归纳:
- 如果 \(S = \operatorname{\mathtt{Top}}\) 或 \(T = \operatorname{\mathtt{Top}}\),那么 \(S \wedge T\) 的结果一定是 \(T\) 或 \(S\)
- 如果 \(S = \operatorname{\mathrm{Bool}}\) 且 \(T = \operatorname{\mathrm{Bool}}\),那么 \(S \wedge T = \operatorname{\mathrm{Bool}}\)
- 如果 \(S = S_1 \to S_2\) 且 \(T = T_1 \to T_2\)。由于 \(\vee\) 是 total 的,那么必定存在 \(J₁\) 使得 \(S_1 \vee T_1 = J_1\)。根据 inversion lemma,\(L\) 的形式必定为 \(L₁ \rightarrow L₂\),并且 \(L₂ <: S₂\) 和 \(L₂ <: T₂\)。根据归纳假设,\(S₂ \wedge T₂\) 不会
fail,设 \(S₂ \wedge T₂ = M₂\)。那么 \(S \wedge T = J₁ \to M₂\) - 如果 \(S = \{k_j : S_j^{j \in 1 \dots m}\}\) 且 \(T = \{l_i : T_i^{i \in 1 \dots n}\}\)。根据 inversion lemma,\(L\) 必须是一个 record,其标签包括在 S 和 T 中出现的所有标签;对于 S 和 T 中的每个公共标签,根据 inversion lemma \(L\) 中的相应字段是 \(S\) 和 \(T\) 中字段的共同子类型
这个 lemma 表明如果两个类型有下界,则它们一定有 meets。
下面证明上面的算法确实计算出了 joins 和 meets:
- If \(S \vee T = J\), then \(S <: J\) and \(T <: J\).
- If \(S \wedge T = M\), then \(M <: S\) and \(M <: T\).
直接根据算法递归的层次(即调用 \(\vee\) 和 \(\wedge\) 的次数)进行归纳即可。
References
由于 references 是不变的,因此对于 \(S = \operatorname{\mathrm{Ref}}(S₁)\) 和 \(T = \operatorname{\mathrm{Ref}}(T₁)\) 有 \(S \vee T = \operatorname{\mathrm{Ref}}(S₁)\ \operatorname{\mathrm{or}}\ \operatorname{\mathrm{Ref}}(T₁)\) 当且仅当 \(S₁ <: T₁\) 且 \(T₁ <: S₁\)。同理,\(S \wedge T = \operatorname{\mathrm{Ref}}(S₁)\ \operatorname{\mathrm{and}}\ \operatorname{\mathrm{Ref}}(T₁)\) 当且仅当 \(S₁ <: T₁\) 且 \(T₁ <: S₁\)。
但是如果通过 Source 和 Sink 来表示 references,那么这个 subtyping 关系中将不会存在 joins 和 meets。例如类型 \(\operatorname{\mathrm{Ref}}\{a:\operatorname{\mathrm{Nat}},b:\operatorname{\mathrm{Bool}}\}\) 和 \(\operatorname{\mathrm{Ref}}\{a:\operatorname{\mathrm{Nat}}\}\) 都是 \(\operatorname{\mathrm{Source}}\{a:\operatorname{\mathrm{Nat}}\}\) 和 \(\operatorname{\mathrm{Sink}}\{a:\operatorname{\mathrm{Nat}},b:\operatorname{\mathrm{Bool}}\}\) 的子类型,但是它们没有共同的下界。
对于这个问题的一个解决方案是在类型系统中只加入 Source 或 Sink 二者之一。假设只加入 Source,那么有:
\[ S \vee T = \begin{cases} & \dots && \\ & \operatorname{\mathrm{Source}}(J) && \text{if $S = \operatorname{\mathrm{Ref}}(S_1)$, $T = \operatorname{\mathrm{Ref}}(T_1)$, $J = S_1 \vee T_1$} \\ & \operatorname{\mathrm{Source}}(J) && \text{if $S = \operatorname{\mathrm{Source}}(S_1)$, $T = \operatorname{\mathrm{Ref}}(T_1)$, $J = S_1 \vee T_1$} \\ & \operatorname{\mathrm{Source}}(S_1) && \text{if $S = \operatorname{\mathrm{Ref}}(S_1)$, $T = \operatorname{\mathrm{Source}}(T_1)$, $J = S_1 \vee T_1$} \\ & \operatorname{\mathrm{Source}}(S_1) && \text{if $S = \operatorname{\mathrm{Source}}(S_1)$, $T = \operatorname{\mathrm{Source}}(T_1)$, $J = S_1 \vee T_1$} \\ & \dots \end{cases} \]
另一种解决方案是细化 Ref,使其接受两个参数:\(\operatorname{\mathrm{Ref}}(S, T)\) 存储类型 \(S\) 并读取类型 \(T\)。新的 Ref 在其第一个参数上是逆变的,在其第二个参数上是协变的。此时 \(\operatorname{\mathrm{Sink}}\ S \overset{\text{def}}{=} \operatorname{\mathrm{Ref}}\ S\ \operatorname{\mathtt{Top}}\) ,而 \(\operatorname{\mathrm{Source}}\ T \overset{\text{def}}{=} \operatorname{\mathrm{Ref}}\ \operatorname{\mathtt{Bot}}\ T\)。
Add Bot
如果加入 minimal type \(\operatorname{\mathtt{Bot}}\),需要对上面的规则进行扩展:
\[\mapsto \operatorname{\mathtt{Bot}} <: T \tag{SA-Bot}\]
\[\dfrac{\Gamma \vdash t_1 : \operatorname{\mathtt{Bot}} \qquad \Gamma \vdash t_2 : T_2}{\Gamma \vdash t_1\ t_2 : \operatorname{\mathtt{Bot}}} \tag{TA-AppBot}\]
\[\dfrac{\Gamma \vdash t_1 : \operatorname{\mathtt{Bot}}}{\Gamma \vdash t_1.l_i : \operatorname{\mathtt{Bot}}} \tag{TA-ProjBot}\]
考虑 Bot 出现在 if 的条件中的情况,那么需要加入规则:
\[\dfrac{\Gamma \vdash t_1 : \operatorname{\mathtt{Bot}} \qquad \Gamma \vdash t_2 : T_2 \qquad \Gamma \vdash t_3 : T_3}{\Gamma \vdash \operatorname{\mathtt{if}}\ t_1\ \operatorname{\mathtt{then}}\ t_2\ \operatorname{\mathtt{else}}\ t_3 : T} \tag{TA-IfBot}\]
注意这里不应该让表达式返回 \(\operatorname{\mathtt{Bot}}\),