Subtyping 也称为 subtype polymorphism。之前介绍的特性之间基本都是正交的,但是 subtyping 的加入会影响到所有目前已经实现的特性。Subtyping 一般会在 OO 语言中发现。
本章所介绍的语言记作 \(\lambda_{<}\),包含 STLC + subtyping + records。
Subsumption
不加入 subtyping 的 STLC 的类型检查非常严格,例如会拒绝下面这个表达式:
\[ (\lambda r : \{x : \operatorname{\mathtt{Nat}}\}.\ r.x) \{x=0 ,y=1\} \]
尽管根据求值规则,这个表达式是可以进行求值的。加入 subtyping 后,令 \(\{x : \operatorname{\mathtt{Nat}}\}\) 为 \(\{x : \operatorname{\mathtt{Nat}}, y : \operatorname{\mathtt{Nat}}\}\) 的子类型即可解决这个问题。
(subtyping) (principle of safe substitution)
\(S\) is a subtype of \(T\), written \(S <: T\), to mean that any term of type \(S\) can safely be used in a context where a term of type \(T\) is expected.
看待 principle of safe substitution 的另一个有趣的视角是将其看作一种受限的 implicit coercion。
\(S <: T\) 读作 “S is a subtype of T” 或 “T is a supertype of S”。
对应的类型规则被称为 the rule of subsumption:
\[ \dfrac { \Gamma \vdash t : S \quad S <: T } { \Gamma \vdash t : T } \tag{T-Sub} \]
The Subtype Relation
下面分别考虑函数类型和 record types 在 subtyping 下的规则。
The Subtyping relation is a preorder
首先,subtyping 满足下面的规则:
\[ S <: S \tag{S-Refl} \]
\[ \dfrac { S <: U \quad U <: T } { S <: T } \tag{S-Trans} \]
但是 subtying 并不是一个偏序关系,而是一个预序关系,因为它没有反对称性(见 S-RcdPerm)。
此外,通常会令 \(\operatorname{\mathtt{Top}}\) 为所有类型的 supertype,即:
\[S <: \operatorname{\mathtt{Top}} \tag{S-Top}\]
Record Type
对于不同长度的 record types,有 width subtyping rule:
\[ \{ l_i : T_i^{i \in 1 \dots n+k}\} <: \{ l_i : T_i^{i \in 1 \dots n}\} \tag{S-RcdWidth} \]
此处比较特殊的是更长的 record type 在子类型层次上的层级更低,这是因为更长的类型描述了更多的信息,因而能够描述的值就更少。
此外,同样长度的 record types 之间也存在子类型关系:
\[ \dfrac { \forall i. S_i <: T_i } { \{ l_i : S_i^{i \in 1 \dots n} \} <: \{ l_i : T_i^{i \in 1 \dots n} \} } \tag {S-RcdDepth} \]
最后一条是 record types 中 labels 的顺序不影响类型表达:
\[ \dfrac { \{k_j : S_j^{j \in 1 \dots n}\} \text{ is a permutation of } \{l_i : T_i^{i \in 1\dots n}\} } { \{k_j : S_j^{j \in 1 \dots n}\} <: \{l_i : T_i^{i \in 1 \dots n}\} } \tag{S-RcdPerm} \]
这条规则表明 subtyping 并不具备反对称性。
这三条规则还可以结合成一个单一规则,这会在后面会讨论。
Arrow Type
函数类型之间也存在 subtyping 关系:
\[ \dfrac { T_1 <: S_1 \quad S_2 <: T_2 } { S_1 \rightarrow S_2 <: T_1 \rightarrow T_2 } \tag {S-Arrow} \]
其中参数类型是逆变的,结果类型是协变的。对这条规则的一个直观理解如下:
- 参数类型用于接收值。根据 principle of safe substitution,子类型中 \(S_1\) 需要能够接收父类型中的 \(T_1\),因此 \(T_1 <: S_1\)
- 结果类型用于给出值。根据 principle of safe substitution,子类型中 \(S_2\) 需要小于父类型中的 \(T_2\),因此 \(S_2 <: T_2\)
能不能给出一个无限下降序列 \(S_0, S_1, \dots\) 使得 \(\forall i. S_i <: S_{i+1}\)?
类似的,能不能给出一个无限上升序列 \(T_{i}\)?
无限下降序列的构造很简单:
\begin{aligned} & S_0 = \{\} \\ & S_1 = \{a_1 : \operatorname{\mathtt{Top}}\} \\ & S_2 = \{a_1 : \operatorname{\mathtt{Top}}, a_2 : \operatorname{\mathtt{Top}}\} \\ & \dots \end{aligned}
无限上升序列可以用 function type 的 arguments 是 contravariant 的特性:
\[T_i = S_i \rightarrow \operatorname{\mathtt{Top}}\]
Summary

Figure 1: STLC with subtyping
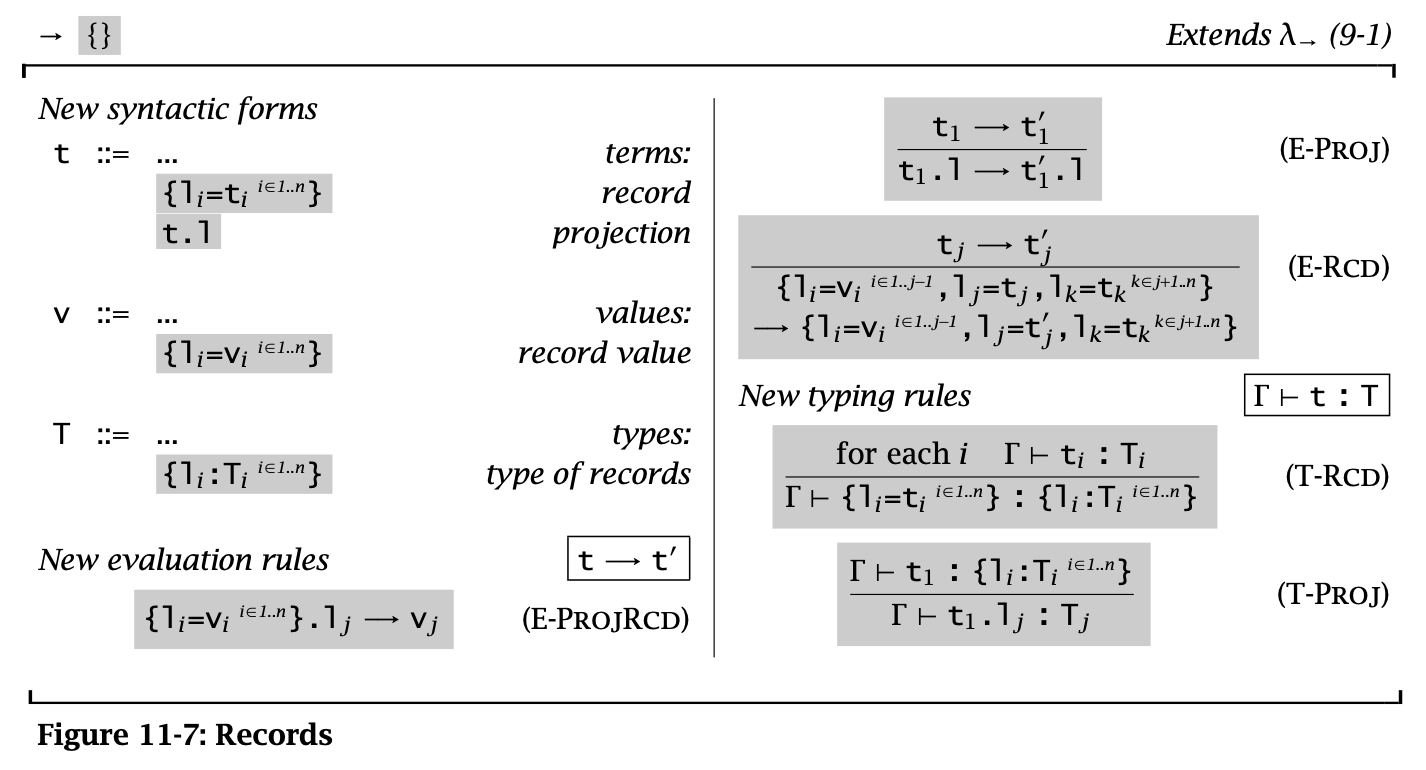
Figure 2: Records
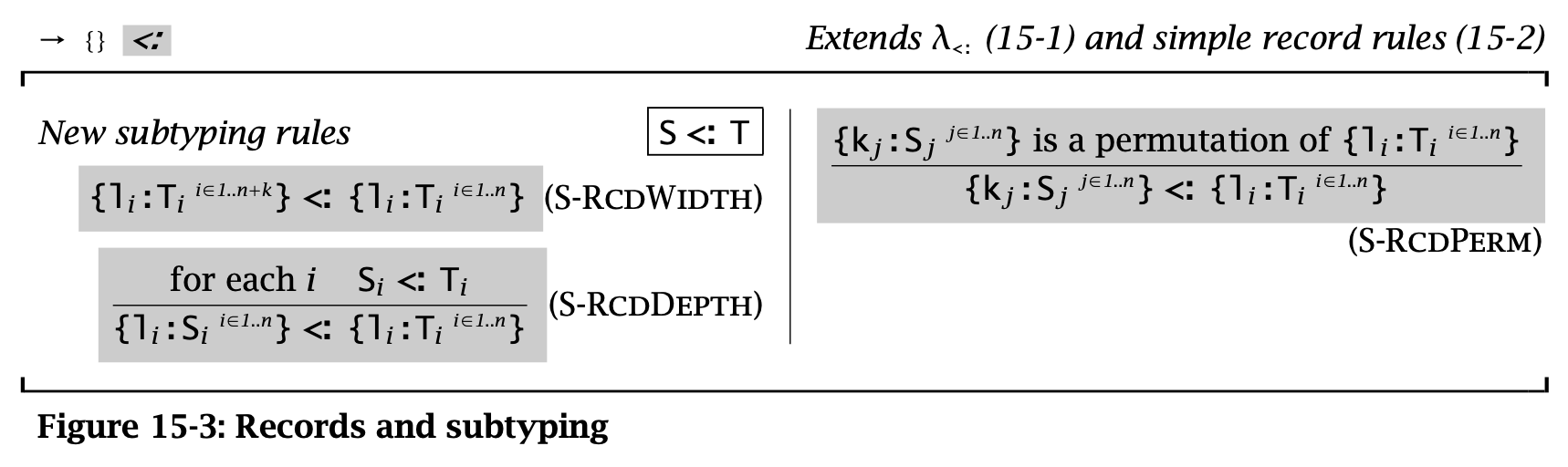
Figure 3: Records and subtyping
在目前的类型系统里面,不存在一个是所有类型 subtype 的类型。
Properties of Subtyping and Typing
Inversion
(Inversion of the subtype relation)
- If \(S <: T_1 \rightarrow T_2\), then \(S\) has the form \(S_1 \rightarrow S_2\), with \(T_1 <: S_1\) and \(S_2 <:T_2\).
- If \(S <: \{l_i : T_i^{i \in 1 \dots n}\}\), then \(S\) has the form \(\{k_j : S_j^{j \in 1 \dots m}\}\), with at least the labels \(\{l_i^{i \in 1 \dots n}\}\) — i.e., \(\{l_i^{i \in 1 \dots n}\} \subseteq \{k_j^{j \in 1 \dots m}\}\)—and with \(S_j <: T_i\) for each common label \(l_i = k_j\).
下面主要考虑第一条的证明,第二条的证明类似:
考虑 \(S <: T_1 \rightarrow T_2\) 的推导中最后一步可能使用的规则:
S-Refl:immediatelyS-Trans:那么\(\exists U. S <: U \wedge U <: T_1 \rightarrow T_2\)- 对第二个条件使用归纳规则,有 \(U : U_1 \rightarrow U_2 \text{ where } T_1 <: U_1 \wedge U_2 <: T_2\)
- 此时再对第一个条件使用归纳规则,有 \(S : S_1 \rightarrow S_2 \text{ where } U_1 <: S_1 \wedge S_2 <: U_2\)
- 使用
S-Trans有 \(S <: T_1 \rightarrow T_2\),且 \(T_1 <: S_1 \wedge S_2 <: T_2\)
S-Arrow:immediately
因为证明的长度是有穷的,而第一步不可能用 S-Trans,因此这个证明成立。
Preservation
为了证明 preservation theorem,还需要以下几个 lemma:
首先需要分别证明以下两个 lemmas:
- If \(\Gamma \vdash (\lambda x : S_1 . s_2) : T_1 \rightarrow T_2\), then \(T_1 <: S_1\) and \(\Gamma, x : S_1 \vdash s_2 : T_2\).
- If \(\Gamma \vdash \{ k_a = s_a^{a \in 1 \dots m}\} : \{l_i : T_i^{i \in 1 \dots n}\}\), then \(\{l_i^{i \in 1 \dots n}\} \subseteq \{k_a^{a \in 1 \dots m}\}\) and \(\Gamma \vdash s_a : T_i\) for each common label \(k_a = l_i\).
对条件的 type derivations 进行归纳即可。对 T-Sub 部分使用上一节中的 lemma。
(Substitution)
If \(\Gamma, x : S \vdash t : T\) and \(\Gamma \vdash s : S\), then \(\Gamma \vdash [x \mapsto s]t : T\).
相比 STLC 中证明的 substitution lemma,这里需要多考虑 T-Sub、T-Rcd 和 T-Proj。
(Preservation)
If \(\Gamma \vdash t : T\) and \(t \rightarrow t’\), then \(\Gamma \vdash t’ : T\).
Induction on typing derivations.
T-Var/T-Abs:已经是 valueT-App:只能用E-App1、E-App2或E-AppAbs\[ t = t_1\ t_2 \quad \text{where}\ \Gamma \vdash t_1 : T_{11} \rightarrow T_{12}, \Gamma \vdash t_2 : T_{11}, T = T_{12} \]
E-App1/E-App2:类似 STLC,根据归纳假设成立E-AppAbs\begin{aligned} & t_1 = \lambda x : S_{11}. t_{12} \\ & t_2 = v_2 \\ & t’ = [x \mapsto v_2] t_{12} \end{aligned}
- 根据 lemma,有 \(T_{11} <: S_{11}\) 且 \(\Gamma, x : S_{11} \vdash s_2 : T_{12}\)
- 根据
T-Sub,有 \(\Gamma \vdash t_2 : T_{11} <: S_{11}\) - 由 substitution lemma,有 \(\Gamma \vdash t’ : T_{12}\)
T-Rcd\[t = \{l_i = t_i ^{i \in 1 \dots n}\} \quad \text{where } \forall i. \Gamma \vdash t_i : T_i, T = \{l_i : T_i ^{i \in 1 \dots n}\}\]
使用
E-Rcd,根据归纳假设,\(t_j \rightarrow t_j’ : T_i\)T-Proj\[t = t_1.l_j \quad \text{where } \Gamma \vdash t_1 : \{l_i : T_i ^{i \in 1 \dots n}\}, T = T_j\]
E-Proj:\(t_1 \rightarrow t_1’ \quad t’ = t_1’.l_j\),根据归纳假设 \(t_1’ : \{l_i : T_i ^{i \in 1 \dots n}\}\)E-ProjRcd\(t_1 = \{k_a = v_a ^{a \in 1 \dots m}\} \quad \text{where } l_j = k_b, t’ = v_b\)
- 根据 lemma,有 \(\{l_{i}^{i \in 1 \dots n}\} \subseteq \{k_{a}^{a \in 1 \dots m}\}\) 且 \(\forall k_{a} = l_{i}. \Gamma \vdash v_a : T_i\),因此 \(\Gamma \vdash v_b : T_j\)
T-Sub:\(t : S, S <: T\),根据归纳假设 \(t’ : S <: T\)
Progress
(Canonical Forms)
- If \(v\) is a closed value of type \(T_1 \rightarrow T_2\), then \(v\) has the form \(\lambda x : S_1. t_2\) with \(T_1 <: S_1\)
- If \(v\) is a closed value of type \(\{l_i : T_i^{i\in1 \dots n}\}\), then \(v\) has the form \(\{k_a = v_a^{a \in 1 \dots m}\}\) with \(\{l_i^{i \in 1 \dots n}\}\subseteq \{k_a^{a \in 1 \dots m}\}\).
Induction on typing derivations, using inversion lemma for T-Sub.
If \(t\) is a closed, well-typed term, then either \(t\) is a value or else there is some \(t’\) with \(t \rightarrow t’\).
Induction on typing derivations.
T-Var:不可能,因为 \(t\) 是封闭的T-Abs:已经是 valueT-App:\begin{aligned} & (t : T_{12}) = t_{1} t_{2} \\ & \vdash t_{1} : T_{11} \rightarrow T_{12} \\ & \vdash t_{2} : T_{11} \end{aligned}
如果能用
E-App1或E-App2,则能继续求值;否则 \(t_1\) 和 \(t_2\) 都是 values,根据 canonical forms lemma,\(v_1 = \lambda x : S_{11}. t_2\) 且 \(T_{11} <: S_{11}\),又 \(v_2 : T_{11}\),因此可以使用E-AppAbsT-Rcd:如果继续求值,则用E-Rcd;否则 \(t\) 已经是一个 valueT-Proj:\begin{aligned} & t = t_1.l_j \\ & \vdash t_1 : \{l_i : T_i ^{i \in 1 \dots n}\} \end{aligned}
如果 \(t\) 不是 value,则用
E-Proj;否则根据 Canonical form lemma,有 \(\{k_a = v_a^{a \in 1 \dots m}\}\) 且 \(\{l_i^{i \in 1 \dots n}\}\subseteq \{k_a^{a \in 1 \dots m}\}\),因此 \(l_j \in \{k_a^{a \in 1 \dots m}\}\),因此可以使用E-ProjRcdT-Sub:根据归纳假设,成立
The Top and Bottom Types
Top 类型(maximal type)在 STLC with subtyping 中不是必须的,但是定义中经常会包含它,包括以下几个原因:
- 它对应了 OO 语言中的
Object类型 - 在包含 subtyping 和 parametric polymorphism 的类型系统中通常会包含
Top,利用它能够从 bounded quantification 中恢复原来的 unbounded quantification
下面讨论 bottom type(minimal type),将其加入现有的类型系统并不会破坏类型系统的性质。
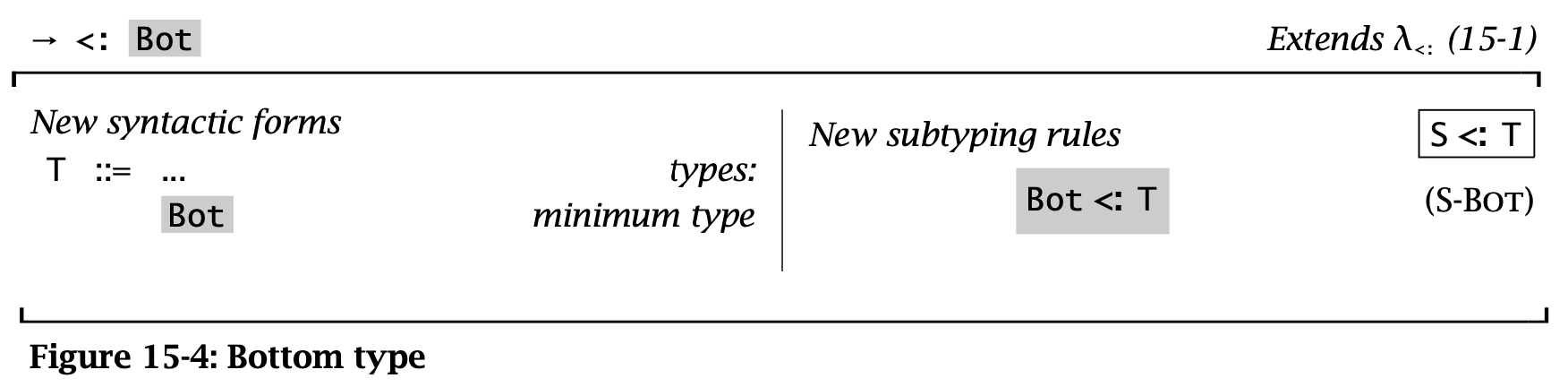
Figure 4: Bottom type
如果 bottom type 存在,那么其值应当是空的。否则设 \(\vdash v : \operatorname{\mathtt{Bot}} <: \operatorname{\mathtt{Top}} \rightarrow \operatorname{\mathtt{Top}}\),那么根据 canonical forms,\(v\) 一定具有类似 \(\lambda x : S_1. t_2\) 的形式。同理,从 record type 的角度还可以得到 \(\vdash v :\operatorname{\mathtt{Bot}} <: \{\}\),则 \(v\) 是一个 record。矛盾。因此 \(v\) 不存在。
将 bottom type 加入类型系统有以下两方面的好处:
- 由于 bottom type 中没有值,因此它可以用来表达一个不会返回的函数;
- 由于 bottom type 是任意类型的 subtype,因此它可以用在任何位置
例如在异常中令
error的返回类型为Bot,则可以写出下面的 term\[ \lambda x : T. \operatorname{\mathtt{if}} \text{ $\langle$check x is reasonable$\rangle$ } \operatorname{\mathtt{then}} \text{ $\langle$computation$\rangle$ } \operatorname{\mathtt{else}}\ \operatorname{\mathtt{error}} \]
在实现 polymorphism 的语言中通常令其为 \(\forall X. X\)
但是加入 Bot 会使类型推导算法和类型系统性质的证明变得更加复杂。例如在考虑 \(t_1\ t_2\) 中 \(t_1\) 的类型时,不仅需要考虑 arrow type 的情况,还要考虑 Bot 的情况。
因此在本书的剩余部分不会再考虑 Bot。
Subtyping and Other Features
由于 subtyping 的加入会影响到其他特性,因此在 \(\lambda_{<}\) 中加入新特性前需要认真考虑每个类型。
Ascription and Casting
在 Java 或 C++ 等语言中,ascription 被用作 casting,写作 (T) t。Casting 分为 up-casts 和 down-casts:
Up-casts 中,term 被 ascribed 成 supertype。在这种情况下,typechecker 会利用
T-Sub和前面给出的T-Ascribe来推导类型,不需要添加额外的规则。Up-casts 可以看作一种“抽象”,它可以用作在当前的上下文中隐藏当前 term 的一些信息,例如隐藏 records 中的 field 或者 objects 的 methods\[ \dfrac{ \dfrac{ \dfrac{\dots}{\Gamma \vdash t : S} \quad \dfrac{\dots}{S <: T} }{ \Gamma \vdash t : T } \text{T-Sub} }{ \Gamma \vdash t\ \operatorname{\mathtt{as}}\ T : T } \text{T-Ascribe} \]
Down-casts 用于为 typechecker 无法静态推导出的类型信息。为了实现 down-casts,需要添加下面这条规则让用户可以任意添加 down-casts 信息
\[ \dfrac{ \Gamma \vdash t_1 : S }{ \Gamma \vdash t_1\ \operatorname{\mathtt{as}}\ T : T } \tag{T-Downcast} \]
这使得 typechecker 无法在静态分析的时候保证系统的稳健性,因此通常语言会在运行时添加额外的类型检查(dynamic type-testing),即添加下面这条 evaluation 规则:
\[ \dfrac{ \vdash v : T } { v\ \operatorname{\mathtt{as}}\ T \rightarrow v } \tag{E-Downcast} \]
添加了 down-casts 之后,类型系统的 progress 性质被破坏,因为用户给出的 down-casts 规则可能导致 evaluation 的过程 stuck。在支持 down-casts 的语言中通常提供了两种解决方案:
转换失败时引发一个异常来避免程序 stuck
使用 dynamic type test 来实现 down-casts。规则如下所示:
\[ \dfrac{ \Gamma \vdash t_1 : S \quad \Gamma, x : T \vdash t_2 : U \quad \Gamma \vdash t3 : U }{ \Gamma \vdash (\operatorname{\mathtt{if}}\ t_1\ \operatorname{\mathtt{in}}\ T\ \operatorname{\mathtt{then}}\ x \rightarrow t_2\ \operatorname{\mathtt{else}}\ t_3) : U } \tag{T-Typetest} \]
\[ \dfrac{ \vdash v_1 : T }{ (\operatorname{\mathtt{if}}\ v1\ \operatorname{\mathtt{in}}\ T\ \operatorname{\mathtt{then}}\ x \rightarrow t_2\ \operatorname{\mathtt{else}}\ t_3) \rightarrow [x \mapsto v_1] t_2 } \tag{E-Typetest1} \]
\[ \dfrac{ \nvdash v_1 : T }{ (\operatorname{\mathtt{if}}\ v_1\ \operatorname{\mathtt{in}}\ T\ \operatorname{\mathtt{then}}\ x \rightarrow t_2\ \operatorname{\mathtt{else}}\ t_3) \rightarrow t_3 } \tag{E-Typetest2} \]
早期的 Java 中使用 down-casts 实现类似了简陋的 polymorphism。例如 Java 中的 List 实际上是 List Object。在使用时从中取出元素需要手动 down-cast 到之前的类型。尽管这样让程序变得不安全,但是这样能在不实现 polymorphism 的情况下实现泛型,简化了类型系统设计。
Down-casts 也在 Java 的反射中起到了重要作用。通过反射,程序能够动态地加载类并创建对象。而创建出的对象的类型在静态期是无法分析的,因此它们的默认类型都是 Object。因此需要通过 down-casts 将其转换到需要的类型以使用。
由于 down-casts 需要让程序进行动态类型检查,这使得编译出的程序包含了一套类型检查程序,让程序变得更加复杂。为了解决这个问题,语言会通过 type tags 来实现 down-casts(类似 data constructor)。Type tags 会为变量保存其实际类型,以简化动态类型检查的过程。
Variants
Variants 可以看作和 records 是对偶的,因此其规则也和 record types 对应。区别在于在 record types 中 fields 较少的类型“更大”,而 variants 中 fields 更多的类型“更大”。
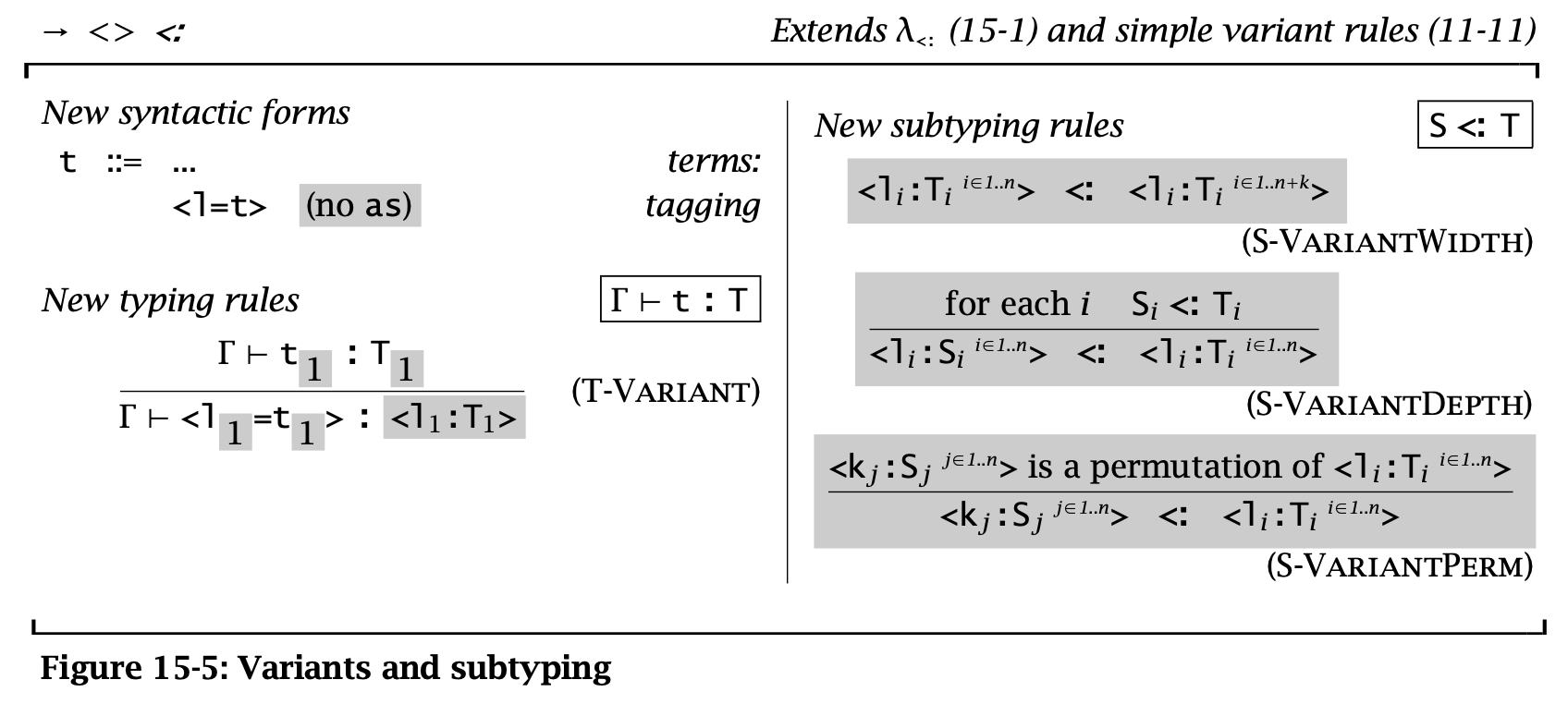
Figure 5: Variants and subtyping
加入了 subtyping for variants 后,使用 variants 时可以变得更方便:不需要每次都写使用 \(\langle l=t \rangle \ \operatorname{\mathtt{as}}\ \langle l_i : T_i^{i \in 1 \dots n} \rangle\),只需要写 \(\langle l = t \rangle\) 然后利用 S-VariantWidth 即可。
Lists
Lists 类似 records、variants 和函数的结果类型,都是共变函子(而函数的参数类型是反变函子):
\[ \dfrac{ S_1 <: T_1 }{ \operatorname{\mathtt{List}}\ S_1 <: \operatorname{\mathtt{List}}\ T_1 } \tag{S-List} \]
这里提到的 Lists 是 immutable 的,因此可以安全地进行共变。反之如果是 mutable 的,就应该设计成 invariant。
Reference
Invariant
Ref 既不是共变函子,也不是反变函子,而是一个不变函子:
\[ \dfrac { S_1 <: T_1 \quad T_1 <: S_1 } { \operatorname{\mathtt{Ref}}\ S_1 <: \operatorname{\mathtt{Ref}}\ T_1 } \tag{S-Ref} \]
两个 reference 有子类型关系仅当它们在子类型关系中是等价的。例如对于在 record type 中,labels 的顺序变换不改变它们在子类型中的等价性:\(\operatorname{\mathtt{Ref}}\ \{a : \operatorname{\mathtt{Bool}}, b : \operatorname{\mathtt{Nat}}\} <: \operatorname{\mathtt{Ref}} \{b : \operatorname{\mathtt{Nat}}, a : \operatorname{\mathtt{Bool}}\}\)。
Reference type 的 subtyping 规则之所以这么受限,是因为它们有两种操作:读取(!)和赋值(:=)。设 \(\operatorname{\mathtt{Ref}}\ S_1\),进行读取时希望得到 \(T_1\),则 \(S_1 <: T_1\)(即读取到的类型应当比期望的更小);写入时提供的类型为 \(T_1\),则需要 \(T_1 <: S_1\)(即写入的类型应当比允许的更小)。
Array
前面的 arrays 是 references 实现的,因此 arrays 也是 invariant 的。
\[ \dfrac{ S_1 <: T_1 \quad T_1 <: S_1 } { \operatorname{\mathtt{Array}}\ S_1 <: \operatorname{\mathtt{Array}}\ T_1 } \tag{S-Array} \]
在 Java 中,数组是协变的:\([S_1] <: [T_1]\)。这是为了在缺少 parametric polymorphism 的情况下实现一些基本的操作。但是现在这个特性已经被认为是错误的,因为它会导致每次对数组进行写操作时都要进行动态类型检查,并导致程序的运行效率降低。
A more refined rules (sources and sinks)
为了让 references 的分析更加精细化,可以将其两种操作分开来:
- \(\operatorname{\mathtt{Source}}\ T\) 能读但是不能写
- \(\operatorname{\mathtt{Sink}}\ T\) 能写但是不能读
- \(\operatorname{\mathtt{Ref}}\ T\) 是二者的结合
\[ \dfrac{ \Gamma | \Sigma \vdash t_1 : \operatorname{\mathtt{Source}}\ T_{11} } { \Gamma | \Sigma \vdash !t_1 : T_{11} } \tag{T-Deref} \]
\[ \dfrac{ \Gamma | \Sigma \vdash t_1 : \operatorname{\mathtt{Sink}}\ T_{11} \quad \Gamma | \Sigma \vdash t_2 : \ T_{11} } { \Gamma | \Sigma \vdash t_1 := t_2 : \operatorname{\mathtt{Unit}} } \tag{T-Assign} \]
此时 Source 是共变的,Sink 是反变的。
\[ \dfrac{ S_1 <: T_1 }{ \operatorname{\mathtt{Source}}\ S_1 <: \operatorname{\mathtt{Source}}\ T_1 } \tag{S-Source} \]
\[ \dfrac{ T_1 <: S_1 }{ \operatorname{\mathtt{Sink}}\ S_1 <: \operatorname{\mathtt{Sink}}\ T_1 } \tag{S-Sink} \]
由于 references 的功能更多,所以应该让它能够“退化到” sources 或者 sinks,因此应该让 references 成为子类型:
\[\operatorname{\mathtt{Ref}}\ T_1 <: \operatorname{\mathtt{Source}}\ T_1 \tag{S-RefSource}\]
\[\operatorname{\mathtt{Ref}}\ T_1 <: \operatorname{\mathtt{Sink}}\ T_1 \tag{S-RefSink}\]
Channels
Channel types 常见于并发编程语言,它和 reference types 非常相似:一个 channel 可以用于读,也可以用于写。因此 channel types 也是 invariant 的。
但是如果模仿 source types 和 sink types 对 channel types 进行拆分:
- Input channels 即 sources types 是共变的
- Output channels 即 sink types 是反变的
Base types
Base types 之间也可以有 subtyping 的关系,例如常见的 \(\operatorname{\mathtt{Bool}} <: \operatorname{\mathtt{Nat}}\)。
Coercion Semantics for Subtyping
Subtyping 有两种理解方式,一种是前面的 subset semantics,认为父类型所表达的范围包含了子类型。但是这种理解方式在实现时存在一些问题。下面将介绍另一种理解方式:coercion semantics。它认为 subtyping 关系可以看作是 coercion,即隐式类型转换。
Problems with the Subset Semantics
本章中提到的 subtyping 只影响程序的类型推导过程,而不会影响程序的 evaluation 结果。但是 subtyping 可能会带来运行时的效率损失。
- 例如令 \(\operatorname{\mathtt{Int}} <: \operatorname{\mathtt{Float}}\),在实际实现中,二者的实现方式是完全不同的。为了实现这一条 subtyping,必须要对类型进行装箱(tagged or boxed),添加额外的标签标记当前的类型。但是这就导致许多操作都要进行类型检查和拆箱工作,尽管编译器能优化掉一些操作,但是还是会导致性能上的损失。
- Subtyping with permutation rule 也会对 record type 的运行产生影响。在 projection 中,\(\{l_i = v_i^{i \in 1 \dots n}\}.l_j \rightarrow v_j\) 在计算时需要遍历所有标签来找到对应的值。
Coercion Semantics
Coersion semantics 会将一个带 subtyping 的语言翻译到一个不带 subtyping 的低级语言上。在类型检查的时候,如果发现了 subtyping,那么它会利用事先准备好的翻译规则将子类型转换为父类型。
包含 subtyping 的语言的 coercion semantics 可以看作一个函数 \(\llbracket - \rrbracket\),能将其翻译到不带 subtyping 的低级语言(例如 λ 演算或机器码)。这里将带 Unit 类型的 STLC 作为目标语言。规则如下:
\[\llbracket \operatorname{\mathtt{Top}} \rrbracket = \operatorname{\mathtt{Unit}}\]
\[\llbracket T_1 \rightarrow T_2 \rrbracket = \llbracket T_1 \rrbracket \rightarrow \llbracket T_2 \rrbracket \]
\[\llbracket \{l_i : T_i ^{i \in 1 \dots n}\} \rrbracket = \{l_i : \llbracket T_i \rrbracket ^{i \in 1 \dots n}\}\]
在翻译一个 term 的时候,其 type derivation 中用到了 subtyping rules 的地方需要插入 run-time coercions。因此应该根据 type derivations 进行转换,即需要根据 typing rules 编写转换规则。为了能针对不同的 subtyping rules 给出不同的转换规则,这里用函数 \(\llbracket - \rrbracket\) 将 subtyping rules 翻译到其对应的转换规则。
下面给出了 subtyping rules 的转换函数,其中 \(\mathcal{C} :: S <: T\) 表示一个结果为 \(\mathcal{S <: T}\) 的 type derivation \(\mathcal{C}\)。这个函数会将 subtyping rules 映射到一个 coercion。Coercions 是一个目标语言(这里是 \(\lambda_\rightarrow\))上的函数,\(\mathcal{C} :: S <: T\) 会将 \(\llbracket S \rrbracket\) 翻译到 \(\llbracket T \rrbracket\)。
\[\llbracket \dfrac{}{T <: T} \rrbracket = \lambda x : \llbracket T \rrbracket . x\]
\[\llbracket \dfrac{}{S <: \operatorname{\mathtt{Top}}} \rrbracket = \lambda x : \llbracket S \rrbracket . \operatorname{\mathtt{unit}}\]
\[\llbracket \dfrac{\mathcal{C}_1 :: S <: U \quad \mathcal{C}_2 :: U <: T}{S <: T} \rrbracket = \lambda x : \llbracket S \rrbracket . \llbracket \mathcal{C}_2 \rrbracket(\llbracket \mathcal{C}_1 \rrbracket)\ x\]
\[\llbracket \dfrac { \mathcal{C}_1 :: T_1 <: S_1 \quad \mathcal{C}_2 :: S_2 <: T_2 } { S_1 \rightarrow S_2 <: T_1 \rightarrow T_2 } \rrbracket = \lambda f : \llbracket S_1 \rightarrow S_2 \rrbracket . \lambda x : \llbracket T_1 \rrbracket . \llbracket \mathcal{C}_2 \rrbracket (f(\llbracket \mathcal{C}_1 \rrbracket\ x)) \]
\[\llbracket \{ l_i : T_i^{i \in 1 \dots n+k}\} <: \{ l_i : T_i^{i \in 1 \dots n}\} \rrbracket = \lambda r : \{l_i : \llbracket T_i \rrbracket ^{i \in 1 \dots n+k}\}. \{l_i = r.l_i^{i \in 1 \dots n}\}\]
\[\llbracket \dfrac { \forall i. \mathcal{C}_i :: S_i <: T_i } { \{ l_i : S_i^{i \in 1 \dots n} \} <: \{ l_i : T_i^{i \in 1 \dots n} \} } \rrbracket = \lambda r : \{l_i : \llbracket S_i \rrbracket ^ {i \in 1 \dots n}\}. \{l_i = \llbracket \mathcal{C}_i \rrbracket(r.l_i) ^{i \in 1 \dots n}\}\]
\[\llbracket \dfrac { \{k_j : S_j^{j \in 1 \dots n}\} \text{ is a permutation of } \{l_i : T_i^{i \in 1\dots n}\} } { \{k_j : S_j^{j \in 1 \dots n}\} <: \{l_i : T_i^{i \in 1 \dots n}\} } \rrbracket = \lambda r : \{k_j : \llbracket S_i \rrbracket ^{j \in 1 \dots n}\}. \{l_i = r.l_i^{i \in 1 \dots n}\}\]
If \(\mathcal{C} :: S <: T\), then \(\vdash \llbracket \mathcal{C} \rrbracket : \llbracket S \rrbracket \rightarrow \llbracket T \rrbracket\).
类似的,type derivation 也可以这样翻译。\(\mathcal{D} :: \Gamma \vdash t : T\) 的翻译 \(\llbracket \mathcal{D} \rrbracket : \llbracket T \rrbracket\) 是目标语言上的 term \(t\)。这种翻译函数也被称为 Penn translation。
\[\llbracket \dfrac{x : T \in \Gamma}{\Gamma \vdash x : T} \rrbracket = x\]
\[\llbracket \dfrac{\mathcal{D}_2 :: \Gamma, x : T_1 \vdash t_2 : T_2}{\Gamma \vdash \lambda x : T_1 : T_1 \rightarrow T_2} \rrbracket = \lambda x. \llbracket T_2 \rrbracket . \llbracket D_2 \rrbracket\]
\[\llbracket \dfrac{\mathcal{D}_1 :: \Gamma \vdash t_1 : T_{11} \rightarrow T_{12} \quad \mathcal{D}_2 :: \Gamma \vdash t_2 : T_{11}}{\Gamma \vdash t_1\ t_2 : T_{12}} \rrbracket = \llbracket \mathcal{D}_1 \rrbracket \llbracket \mathcal{D}_2 \rrbracket\]
\[\llbracket \dfrac{\forall i. \mathcal{D}_i :: \Gamma \vdash t_i : T_i}{\Gamma \vdash \{l_i = t_i ^{i \in 1 \dots n}\} : \{l_i : T_i ^{i \in 1 \dots n}\}} \rrbracket = \{l_i = \llbracket D_i \rrbracket^{i \in 1 \dots n}\}\]
\[\llbracket \dfrac{\mathcal{D}_1 :: \Gamma \vdash t_1 : \{l_i : T_i^{i \in 1 \dots n}\}}{\Gamma \vdash t_1.l_j : T_j} \rrbracket = \llbracket D_1 \rrbracket .l_j\]
\[\llbracket \dfrac{\mathcal{D} :: \Gamma \vdash t : S \quad \mathcal{C} :: S <: T}{\Gamma \vdash t : T} \rrbracket = \llbracket \mathcal{C} \rrbracket \llbracket \mathcal{D} \rrbracket\]
If \(\mathcal{D} :: \Gamma \vdash t : T\), then \(\llbracket \Gamma \rrbracket \vdash \llbracket \mathcal{D} \rrbracket : \llbracket T \rrbracket\), where \(\llbracket \Gamma \rrbracket\) is the pointwise extension of the type translation to contexts: \(\llbracket \emptyset \rrbracket = \emptyset\) and \(\llbracket \Gamma , x:T \rrbracket = \llbracket \Gamma \rrbracket, x:\llbracket T \rrbracket\).
\[\llbracket \operatorname{\mathtt{Bool}} <: \operatorname{\mathtt{Int}} \rrbracket = \lambda b : \operatorname{\mathtt{Bool}}. \operatorname{\mathtt{if}}\ b\ \operatorname{\mathtt{then}}\ 1\ \operatorname{\mathtt{else}}\ 0\]
\[\llbracket \operatorname{\mathtt{Int}} <: \operatorname{\mathtt{String}} \rrbracket = \operatorname{\mathtt{intToString}}\]
因此
\[\llbracket \operatorname{\mathtt{Bool}} <: \operatorname{\mathtt{String}} \rrbracket = \lambda b : \operatorname{\mathtt{Bool}}. \operatorname{\mathtt{intToString}} (\operatorname{\mathtt{if}}\ b\ \operatorname{\mathtt{then}}\ 1\ \operatorname{\mathtt{else}}\ 0)\]
Coherence
在类型转换的过程中可能会遇到一致性的问题。
例如希望将 \(\operatorname{\mathtt{Bool}}\) 转换到 \(\operatorname{\mathtt{String}}\),并且现在已经有下面四条规则:
\[\llbracket \operatorname{\mathtt{Bool}} <: \operatorname{\mathtt{Int}} \rrbracket = \lambda b : \operatorname{\mathtt{Bool}}. \operatorname{\mathtt{if}}\ b\ \operatorname{\mathtt{then}}\ 1\ \operatorname{\mathtt{else}}\ 0\]
\[\llbracket \operatorname{\mathtt{Int}} <: \operatorname{\mathtt{String}} \rrbracket = \operatorname{\mathtt{intToString}}\]
\[\llbracket \operatorname{\mathtt{Bool}} <: \operatorname{\mathtt{Float}} \rrbracket = \lambda b : \operatorname{\mathtt{Bool}}. \operatorname{\mathtt{if}}\ b\ \operatorname{\mathtt{then}}\ 1.0\ \operatorname{\mathtt{else}}\ 0.0\]
\[\llbracket \operatorname{\mathtt{Float}} <: \operatorname{\mathtt{String}} \rrbracket = \operatorname{\mathtt{floatToString}}\]
那么可能有两种路径:\(\operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Int}} \rightarrow \operatorname{\mathtt{String}}\) 和 \(\operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Float}} \rightarrow \operatorname{\mathtt{String}}\),而使用不同的路径可能会得到不同的结果(例如 true 变成 "1" 或 "1.0")。
为了让语言的行为确定下来,需要为转换函数添加一些强制的要求,称为 coherence。
A translation \(\llbracket - \rrbracket\) from typing derivations in one language to terms in another is coherent if, for every pair of derivations \(\mathcal{D}_1\) and \(\mathcal{D}_2\) with the same conclusion \(\Gamma \vdash t : T\), the translations \(\mathcal{D}_1\) and \(\mathcal{D}_2\) are behaviorally equivalent terms of the target language.
Intersection and Union Types
Intersection types
Intersection type \(T_1 \wedge T_2\) 中的 terms 是两个类型的 terms 的交集,也就是既属于 \(T_1\) 又属于 \(T_2\) 的 terms。相当于其中的 terms 同时具备两个类型的特性,既可以当成 \(T_1\) 用,又可以当成 \(T_2\) 用,同时能进行两种类型的操作。
\[T_1 \wedge T_2 <: T_1 \tag{S-Inter1}\]
\[T_1 \wedge T_2 <: T_2 \tag{S-Inter2}\]
\[\dfrac{ S <: T_1 \quad S <: T_2 }{S <: T_1 \wedge T_2} \tag{S-Inter3}\]
Intersection types 用于 record types 可以合并两个 record types 的 labels:
\[ \{a_i : b_i ^ {i \in 1 \dots n}\} \wedge \{c_i : d_i ^ {i \in 1 \dots m}\} <: \{a_i : b_i ^ {i \in 1 \dots n}, c_i : d_i ^ {i \in 1 \dots m} \} \]
Intersection types 还可以表达函数的有限重载(finitary overloading):\(f : S_1 \rightarrow T_1 \wedge S_2 \rightarrow T_2\) 表示两个函数类型的重载,因此 \(f(s_1 : S_1)\) 和 \(f(s_2 : S_2)\) 都是合法的。
\(\lambda x . x + x : \operatorname{\mathtt{Int}} \rightarrow \operatorname{\mathtt{Int}} \wedge \operatorname{\mathtt{Float}} \rightarrow \operatorname{\mathtt{Float}}\)
Intersection types 在类型检查会穷举每一种可能,对于匹配的某一种可能,将结果通过 \(\wedge\) 合并。因此 Intersection types 作用在 arrow types 上有下面的行为:
\[S_1 \rightarrow T_1 \wedge S_1 \rightarrow T_2 <: S_1 \rightarrow (T_1 \wedge T_2) \tag{S-Inter4} \]
对于一个包含 subtyping 和 intersection type 的系统,其中 typable 的 terms 的集合等价于 normalizing terms 的集合,即包含 intersection type 的演算系统的 type reconstruction 是一个 undecidable 的问题。
Intersection types 的一个受限制情况是 refinement types。其类型中包含了一个 predicate。Refinement types 用在函数的参数类型时可以用于表达函数的 pre-conditions,用作函数的结果类型时可以表达函数的 post-conditions。
Union types
Union types 是 intersection types 的对偶,其描述了两个类型的并集。
显然 \(\operatorname{\mathtt{Nat}} \vee \operatorname{\mathtt{Nat}}\) 等价于 \(\operatorname{\mathtt{Nat}}\)。
Union types 类似 C 语言的 untagged union,无法区分值究竟是属于哪种类型。因此理论上操作 union types 时只能使用其所有类型的操作的交集,这样才不会 stuck。但是 C 语言中的 untagged union 却没有这个限制,因为 C 语言的 untagged union 时 unsafe 的。