本章讨论的是 STLC + Unit + References 的类型系统。
注意本章中描述的 references 不是指 C++ 中的引用类型,而是指一个存了值的 cell,其中 cell 的值可读可写,所以两次读出来的值可能不同。即 references 可以理解为可变类型。
Introduction
在 ML 系语言中变量分为两种,一种是拥有值的常量,另一种是拥有 cell 的变量。
对于前者而言可以直接将其用作运算 x + 5,但是不能向其赋值。对于后者而言可以直接向其赋值 y:=10,但是不能将其用于运算。如果要将其用作运算就必须进行 dereference,即 !y + 5。
在 C/Java 当中可以将所有的变量看作是 references,其和 ML 系语言的区别有两点:
- C/Java 中 references 的 deref 过程是 implicit 的,即使用 cell 中的值不需要显式解引用(但是可以把 C 语言中的指针看成是 References)
- C/Java 中的变量允许
null值存在,所以实际上是一种Option<Ref<T>>类型
Basics
References 有三种基本操作:allocation,的dereferencing 和 assignment。
allocation
\begin{aligned} r &= \operatorname{\mathtt{ref}}\ 5; \\ r &: \operatorname{\mathtt{Ref}}\ \operatorname{\mathtt{Nat}} \\ \end{aligned}
Dereferencing
\[!r : \operatorname{\mathtt{Nat}}\]
assignment
\[r := 7;\]
注意 assignments 的返回值为 unit。
Side Effects and Sequencing
由于 assignments 的值为 unit,则可以利用 sequencing 写,使得语句顺序执行:
\[ (r := \operatorname{\mathtt{succ}}(!r); r := \operatorname{\mathtt{succ}}(!r); !r); \]
References and Aliasing
两个 references 可以指向同一个 cell,此时对其中一个的修改会影响到另一个,并且二者都称为是这个 cell 的 aliases。
Shared State
Aliases 使得静态分析变得更困难。比如一种特殊的情况:
\[ (r := 1; r := !s); \]
在大多数情况可以认为前者是冗余的,可以被删去;然而如果 \(r\) 和 \(s\) 指向的是同一个 cell,反而后者是冗余的。
Aliases 可以让程序的各个部分共享状态并进行“沟通”,即 shared state,这个可以用来实现“对象”的效果。
References to Compound Types
References 结合函数可以用来实现一个(低效的)数组:
\[ \operatorname{\mathtt{NatArray}} = \operatorname{\mathtt{Ref}}\ (\operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}}); \]
\begin{aligned} \operatorname{\mathtt{newarray}} &= \lambda \_ : \operatorname{\mathtt{Unit}}. \operatorname{\mathtt{ref}}\ (\lambda n : \operatorname{\mathtt{Nat}}. 0); \\ \operatorname{\mathtt{newarray}} &: \operatorname{\mathtt{Unit}} \rightarrow \operatorname{\mathtt{NatArray}} \end{aligned}
\begin{aligned} \operatorname{\mathtt{lookup}} &= \lambda a : \operatorname{\mathtt{NatArray}}. \lambda n : \operatorname{\mathtt{Nat}}. (!a)\ n; \\ \operatorname{\mathtt{lookup}} &: \operatorname{\mathtt{NatArray}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \end{aligned}
\begin{aligned} \operatorname{\mathtt{update}} &= \lambda a : \operatorname{\mathtt{NatArray}}. \lambda m : \operatorname{\mathtt{Nat}}. \lambda v : \operatorname{\mathtt{Nat}}. \\ & \qquad \operatorname{\mathtt{let}}\ oldf = (!a)\ \operatorname{\mathtt{in}} \\ & \qquad \quad a := (\lambda n : \operatorname{\mathtt{Nat}}. \operatorname{\mathtt{if}}\ \operatorname{\mathtt{equal}}\ m\ n\ \operatorname{\mathtt{then}}\ v\ \operatorname{\mathtt{else}}\ oldf\ n); \\ \operatorname{\mathtt{update}} &: \operatorname{\mathtt{NatArray}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Unit}} \end{aligned}
Typing
\[ \dfrac { \Gamma \vdash t_1 : T_1 } { \Gamma \vdash \operatorname{\mathtt{ref}}\ t_1 : \operatorname{\mathtt{Ref}}\ T_1 } \tag{T-Ref} \]
\[ \dfrac { \Gamma \vdash t_1 : \operatorname{\mathtt{Ref}}\ T_1 } { \Gamma \vdash !t_1 : T_1 } \tag{T-Deref} \]
\[ \dfrac { \Gamma \vdash t_1 : \operatorname{\mathtt{Ref}}\ T_1 \quad \Gamma \vdash t_2 : T_1 } { \Gamma \vdash t_1 := t_2 : \operatorname{\mathtt{Unit}} } \tag{T-Assign} \]
Evaluation
使用 ref 时会创造一个新的 cell,表达式的返回值为指向这个 cell 的 reference,这个返回值被称为 store location(类型为 Ref T,相当于一个内存地址),它也是一个 value。
为了形式化 reference,设 \(\mathcal{L}\) 为 store locations 的集合(即 references 的集合),内存是一个从 location 到 values 的部分函数,\(\mu\) 为 stores 的集合(即内存状态)。为了方便起见,这里不考虑不同类型占用空间不同的影响。
在原来的求值规则中加入 references 后,operational semantics 对 abstract machine 的描述就被扩展了。在原来的规则中,机器的状态只能通过 program counter(即 term 本身)描述;扩展后就加入了 stores 的状态 \(\mu\)。References 会影响到所有的求值规则,包括原来不涉及 references 的规则也要将 \(\mu\) 加入进去。
\[ (\lambda x : T_{11}. t_{12})\ v_2 \vert \mu \rightarrow [x \mapsto v_2] t_{12} \vert \mu \tag{E-AppAbs} \]
\[ \dfrac{ t_1 \vert \mu \rightarrow t_1’ \vert \mu' }{ t_1\ t_2 \vert \mu \rightarrow t_1’\ t_2 \vert \mu' } \tag{E-App1} \]
\[ \dfrac{ t_2 \vert \mu \rightarrow t_2’ \vert \mu' }{ v_1\ t_2 \vert \mu \rightarrow v_1\ t_2’ \vert \mu' } \tag{E-App1} \]
上面的第一条中 E-AppAbs 并不会产生 side effects,所以不会改变 \(\mu\)。
同时需要将 store location 纳入到 values 中。
\begin{aligned} v \Coloneqq & & (\text{values}) \\ & \lambda x.t & (\text{abstraction value}) \\ & \operatorname{\mathtt{unit}} & (\text{unit value}) \\ & l & (\text{store location}) \\ \end{aligned}
\begin{aligned} t \Coloneqq & & (\text{terms}) \\ & x & (\text{variable}) \\ & \lambda x.t & (\text{abstraction}) \\ & t\ t & (\text{application}) \\ & \operatorname{\mathtt{unit}} & (\text{constant $\mathtt{unit}$}) \\ & \operatorname{\mathtt{ref}}\ t & (\text{reference creation}) \\ & !t & (\text{dereference}) \\ & t := t & (\text{assignment}) \\ & l & (\text{store location}) \end{aligned}
虽然在 term 和 value 里面添加了 store location 类型,但是在实际的代码中并不一定会出现这种类型,他们可以作为一种 intermediate language 被隐藏起来。
Evaluation Rules
添加了 store location 类型后,就可以对 references 的 evaluation rules 进行描述了。
Dereferencing 的过程总共分成两步:首先要规约 location 本身,然后再进行 dereferencing。Dereferencing 只能对 locations 进行,否则会产生错误(这个由 type safety 保证)。
\[ \dfrac{ t_1 \vert \mu \rightarrow t_1’ \vert \mu' }{ ! t_1 \vert \mu \rightarrow ! t_1’ \vert \mu' } \tag{E-Deref} \]
\[ \dfrac{ \mu(l) = v }{ !l \vert \mu \rightarrow v \vert \mu } \tag{E-DerefLoc} \]
同样,assignment 的过程也分成多步。
\[ \dfrac{ t_1 \vert \mu \rightarrow t_1’ \vert \mu' }{ t_1 := t_2 \vert \mu \rightarrow t_1’ := t_2 \vert \mu' } \tag{E-Assign1} \]
\[ \dfrac{ t_2 \vert \mu \rightarrow t_2’ \vert \mu' }{ v := t_2 \vert \mu \rightarrow v := t_2’ \vert \mu' } \tag{E-Assign2} \]
\[ l := v_2 \vert \mu \rightarrow \operatorname{\mathtt{unit}} \vert [l \mapsto v_2] \mu \tag{E-Assign} \]
这里 \([l \mapsto v_2] \mu\) 表示其他 location 保持不变,只有 \(l\) 这个 cell 的值被更新为 \(v_2\)。
这里的表达式返回 unit 都是为了和 sequencing notation 相匹配。
最后是对于 ref 表达式的规则,需要选一个新的 location,并且更新 \(\mu\) 为 \((\mu, l, \mapsto v)\)。
\[ \dfrac{ t_1 \vert \mu \rightarrow t_1’ \vert \mu' }{ \operatorname{\mathtt{ref}}\ t_1 \vert \mu \rightarrow \operatorname{\mathtt{ref}}\ t_1’ \vert \mu' } \tag{E-Ref} \]
\[ \dfrac{ l \notin dom(\mu) }{ \operatorname{\mathtt{ref}}\ v_1 \vert \mu \rightarrow l \vert (\mu, l \mapsto v_1) } \tag{E-RefV} \]
Garbage Collection
垃圾回收对应了 deallocation 的过程。在很多现代的语言中都采用了垃圾回收,因为手动回收内存很难实现 type safety,容易造成 dangling reference 等问题。而不正确的内存释放操作可能导致取出来的值类型错误,进而导致类型不安全。
下面将建模前面定义的 abstract machine 中的 garbage collection,其作用为去除 \(\mu\) 中的无用 stores。
reachability
首先,使用 GC 的系统中 locations 的数量一定是有限的,即 \(\vert \mathcal{L} \vert\) 是有穷的。因此 locations 会被复用。
记 \(\mathtt{locations}(t)\) 表示 \(t\) 中 locations 组成的集合。下面定义 locations 的 reachability 属性:
- 如果 \(l’ \in \mathtt{locations}(\mu(l))\),则称 \(l’\) is reachable in one step from a location \(l\) in a store \(\mu\)(理解为 \(l’\) 是 \(l\) 所存储的值中的 locations 之一)
- 如果存在一个 locations 序列 \(l, \dots l’\),其中每一个 location 相对于前一个都是 reachable in one step,则称 \(l’\) is reachable from \(l\)
- 定义 \(\mathtt{reachable(t, \mu)}\) 表示 \(\mu\) 内 \(\mathtt{locations}(t)\) 的所有 reachable 的子集
Evaluation Rules for GC
下面定义 GC 的规则:
\[ \dfrac{ \mu’ = \mu\ \text{restricted to $\mathtt{reachable}(t, \mu)$} }{ t \vert \mu \rightarrow_{gc} t \vert \mu' } \tag{E-GC} \]
这个规则表示 \(\mu’\) 的定义为 \(\mathtt{reachable}(t, \mu)\),并且定义域中所有 locations 的值仍然和 \(\mu\) 相同。
同时改变原来的 evaluation 规则,在其中插入 GC 的规则:
\[ \overset{\text{gc}}{\rightarrow}^* \overset{\text{def}}{=} (\rightarrow \cup \rightarrow_{gc})^* \]
注意,这里 GC 只会在最外层进行,因此我们没有在单步的 evaluation 规则上面加入 GC。因为一个表达式内部中左边的值可能被在右边被用到,而 evaluation 的过程是从左到右的,在内部进行 GC 有可能会错误释放值。(这里指的是对于单个表达式进行求值/推导不能直接 GC,即非 sequencing 的情况;对于 sequencing 中多个表达式求值时,不同表达式的中间仍然可以进行 GC)
Justify the refinements
GC 规则不影响求值结果,只是减少了内存占用:
- 如果 \(t \vert \mu \overset{\text{gc}}{\rightarrow}^\ast t’ \vert \mu’’\),则 \(t \vert \mu \rightarrow^\ast t’ \vert \mu’\),其中 \(\vert dom(\mu’) \vert > \vert dom(\mu’’) \vert\)
- 如果 \(t \vert \mu \rightarrow^* t’ \vert \mu’\),则满足两种情况之一:
- \(t \vert \mu \overset{\text{gc}}{\rightarrow}^\ast t’ \vert \mu’’\),并且 \(\vert dom(\mu’’) \vert < \vert dom(\mu’) \vert\)
- \(t \vert \mu\) 的内存耗尽,即 \(t \vert \mu \rightarrow^\ast t’’’ \vert \mu’’’\),此时 \(\mathtt{reachable}(t’’’, \mu’’’) = \mathcal{L}\)
这里只是一种简单的 GC,在实际的 GC 中还要考虑 finalizers(destructor)和 weak pointers(不算入 reference count)等。
Store Typings
首先可以想到一个很直接的 typing rule,包含了四部分:contexts/terms/types/stores。
\[ \dfrac{ \Gamma \vert \mu \vdash \mu(l) : T_1 }{ \Gamma \vert \mu \vdash l : \operatorname{\mathtt{Ref}}\ T_1 } \]
但是这个规则有两个问题:
- 效率不高:每次遇到一个 location 都要重新寻找类型,并且如果其值中包含其他 location,就需要递归推导
- 无法求解递归的情况,例如:
\[ (l_1 \mapsto \lambda x: \operatorname{\mathtt{Nat}}. (!l_2)\ x, \\ \ l_2 \mapsto \lambda x: \operatorname{\mathtt{Nat}}. (!l_1)\ x) \]
实际上 location 在 allocated 时其类型已经固定了,因此可以利用这一点(substitution theorem 和 preserve theorem)。下面引入一个函数将 location 映射到其类型,称为 store typing,用 \(\Sigma\) 表示(相当于存储 locations 对应的值的类型,类似于 \(\mu\),仅用于 typing)。
设 store typing \(\Sigma\) 描述了 store \(\mu\),那么就可以直接通过 \(\Sigma\) 中存储的信息来推导类型。
\[ \dfrac{ \Sigma(l) = T_1 }{ \Gamma \vert \Sigma \vdash l : \operatorname{\mathtt{Ref}}\ T_1 } \tag{T-Loc} \]
但是这种方式要求 evaluation 的过程中对 location 的 assignment 必须是类型安全的(即赋的值必须和类型匹配)。并且在规约 ref 表达式的时候要去更新 \(\Sigma\)。
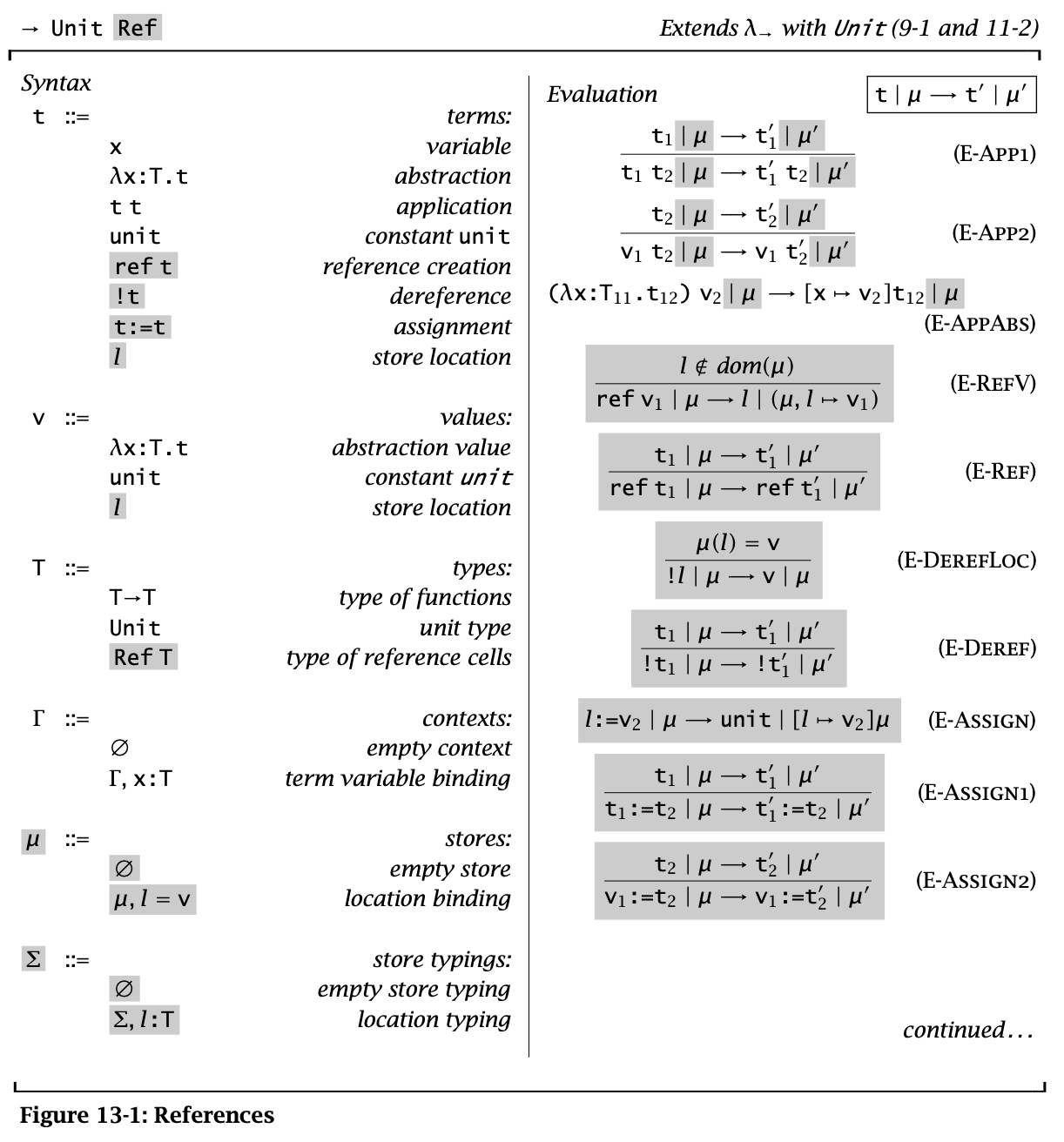
Figure 1: References
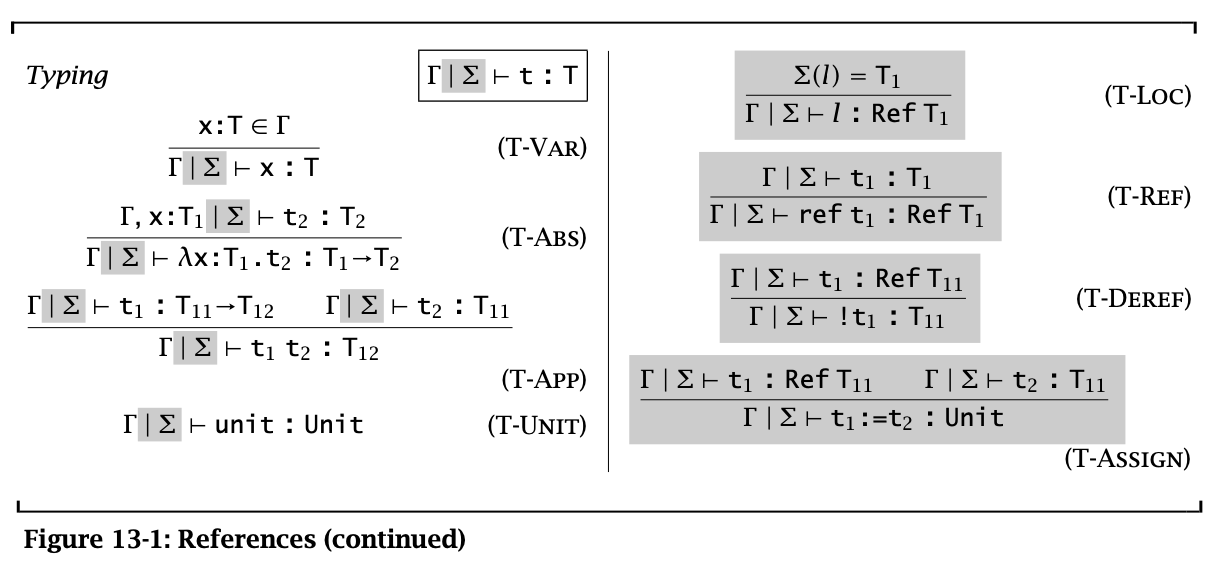
Figure 2: References continue
注意第一幅图左边 store 的规则里的 \(=\) 应该是 \(\mapsto\):
\begin{aligned} \mu \Coloneqq & & & (\text{stores}) \\ & \emptyset & & (\text{empty store}) \\ & \mu, l \mapsto v & & \text{location binding}) \\ \end{aligned}
Safety
Preservation
在表述 preservation theorem 之前,需要明确一些限制。
对于一个 \(\mu\) 和一个 \(\Sigma\),要求二者必须匹配。
(Well typed for references)
A store \(\mu\) is said to be well typed with respect to a typing context \(\Gamma\) and a store typing \(\Sigma\), written
\[\Gamma \vert \Sigma \vdash \mu\]
if \(dom(\mu) = dom(\Sigma)\) and \(\forall l \in dom(\mu). \Gamma \vert \Sigma \vdash \mu(l) : \Sigma(l)\).
除此之外,对于 assignment,要考虑其导致的 \(\Sigma\) 更新的情况。
对于给定的 \(\Gamma\) 和 \(\mu\),能不能找到两个 \(\Sigma_1\) 和 \(\Sigma_2\) 都满足 \(\Gamma \vert \Sigma \vdash \mu\)
\begin{aligned} \Gamma &= \emptyset \\ \mu &= (l \mapsto \lambda x : \operatorname{\mathtt{Unit}}. (!l)(x)) \\ \Sigma_1 &= l : \operatorname{\mathtt{Unit}} \rightarrow \operatorname{\mathtt{Unit}} \\ \Sigma_2 &= l : \operatorname{\mathtt{Unit}} \rightarrow (\operatorname{\mathtt{Unit}} \rightarrow \operatorname{\mathtt{Unit}})\\ \end{aligned}
(Preservation)
If
\begin{aligned} &\Gamma \vert \Sigma \vdash t : T \\ &\Gamma \vert \Sigma \vdash \mu \\ &t \vert \mu \rightarrow t’ \vert \mu' \end{aligned}
then, for some \(\Sigma’ \supseteq \Sigma\) (that is, \(\Sigma’ = \Sigma\) or \(\Sigma’ = (\Sigma, l \mapsto T_1)\))
\begin{aligned} & \Gamma \vert \Sigma’ \vdash t’ : T \\ & \Gamma \vert \Sigma’ \vdash \mu' \end{aligned}
此处的在正式证明 preservation 之前需要几个 lemmas。
(Substitution)
If \(\Gamma, x : S \vert \Sigma \vdash t : T\) and \(\Gamma \vert \Sigma \vdash s : S\), then \(\Gamma \vert \Sigma \vdash [x \mapsto s] t : T\).
If
\begin{aligned} & \Gamma \vert \Sigma \vdash \mu \\ & \Sigma(l) = T \\ & \Gamma \vert \Sigma \vdash v : T \end{aligned}
then \(\Gamma \vert \Sigma \vdash [l \mapsto v] \mu\).
Immediately from definition.
If \(\Gamma \vert \Sigma \vdash t : T\) and \(\Sigma’ \supseteq \Sigma\), then \(\Gamma \vert \Sigma’ \vdash t : T\).
通过以上几个 lemmas 就可以得到 preservation 的证明(模仿 STLC 的证明)。
Store typings 可以当做是为了更方便地证明 preservation theorem 才引入的。
Progress
(Progress)
Suppose \(t\) is a closed, well-typed term (that is, \(\emptyset \vert \Sigma \vdash t : T\) for some \(T\) and \(\Sigma\)). Then either \(t\) is a value or else, for any store \(\mu\) such that \(\emptyset \vert \Sigma \vdash \mu\), there is some term \(t’\) and store \(\mu’\) with \(t \vert \mu \rightarrow t’ \vert \mu’\).
Progress theorem 可以直接模仿 STLC 进行证明。
Recursion via references
References 相关的 evaluation relation 都能 normalize 成 well-typed terms 吗?(即是否都能终止)
不会,尤其是出现 \(r := \lambda x. (!r)\ x\) 的时候,调用 \((!r)\ x\) 会 diverge。
例如:
\begin{aligned} &t_1 = \lambda r : \operatorname{\mathtt{Ref}}(\operatorname{\mathtt{Unit}} \rightarrow \operatorname{\mathtt{Unit}}). \\ & \qquad \qquad (r := (\lambda x : \operatorname{\mathtt{Unit}}. (!r)\ x); \\ & \qquad \qquad \qquad \quad (!r)\ \operatorname{\mathtt{unit}}); \\ & t_2 = \operatorname{\mathtt{ref}} (λx:\operatorname{\mathtt{Unit}}. x); \end{aligned}
则 \(t_1\ t_2\) 会 diverge。
利用 reference 可以定义出 well-typed 的递归函数,一般在函数式语言会这么做。这个过程类似于创建一个指向 abstraction 的 reference \(r\),然后给这个 reference 赋予一个 body,在 body 中调用 \(!r\),就能让函数调用自己了。
以阶乘为例:
Allocate:申请一个
ref并定义一个假的函数体:\begin{aligned} &\operatorname{\mathtt{fact}}_{\operatorname{\mathtt{ref}}} = \operatorname{\mathtt{ref}}\ (\lambda n : \operatorname{\mathtt{Nat}}. 0) \\ &\operatorname{\mathtt{fact}}_{\operatorname{\mathtt{ref}}} : \operatorname{\mathtt{Ref}}\ (\operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}}) \end{aligned}
Define:定义真正的函数体
\begin{aligned} &\operatorname{\mathtt{fact}}_{\operatorname{\mathtt{body}}} = \lambda n : \operatorname{\mathtt{Nat}}. \\ & \quad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ n\ \operatorname{\mathtt{then}}\ 1\ \operatorname{\mathtt{else}}\ \operatorname{\mathtt{times}}\ n\ ((!\operatorname{\mathtt{factor}}_{\operatorname{\mathtt{ref}}})(\operatorname{\mathtt{pred}}\ n)); \\ & \mathtt{fact}_{body} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \end{aligned}
Backpatch:\(\operatorname{\mathtt{fact}}_{\operatorname{\mathtt{ref}}} := \operatorname{\mathtt{fact}}_{\operatorname{\mathtt{body}}}\)
Extract:\(\operatorname{\mathtt{fact}} = !\operatorname{\mathtt{fact}}_{\operatorname{\mathtt{ref}}}\)