类型系统 程序语言理论 程序语义 STLC

[TaPL] 11 Simple Extensions

Posted by roife on Sun, Sep 5, 2021

本章为 STLC 的扩展。

Base Types

Base types 指语言中的一些基础类型，也叫 atomic types，例如 Integer/String/Boolean/Float 等。在理论中，通常用 A 来指代这些 base types，同时用 \(\mathcal{A}\) 表示 base types 组成的集合。

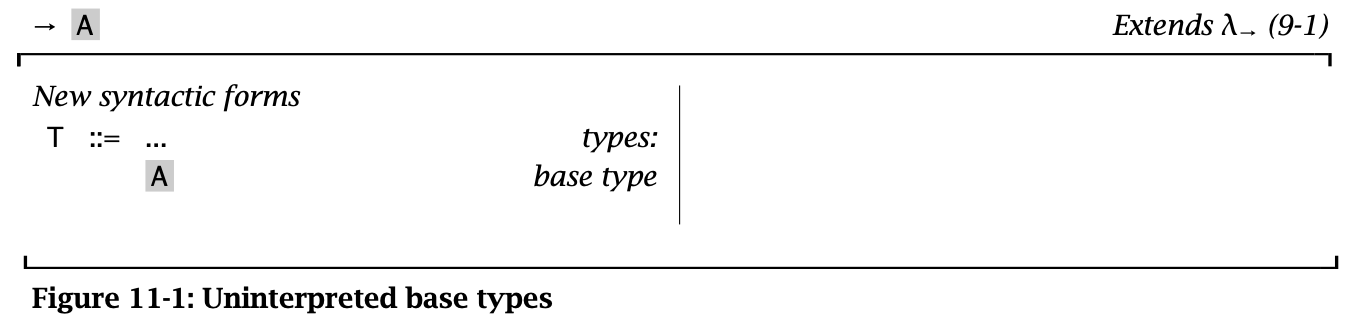
Figure 1: Uninterpreted Base Types

Figure 1: Uninterpreted Base Types

\[ (\lambda f : A \rightarrow A. \lambda x : A. f(f(x))) : (A \rightarrow A) \rightarrow A \rightarrow A \]

The Unit Type

Unit Type 也是一种 Base Type，通常可以在 ML 语言家族中看到。

其特殊之处在于 Unit Type 只有唯一一个 value，即 Unit。

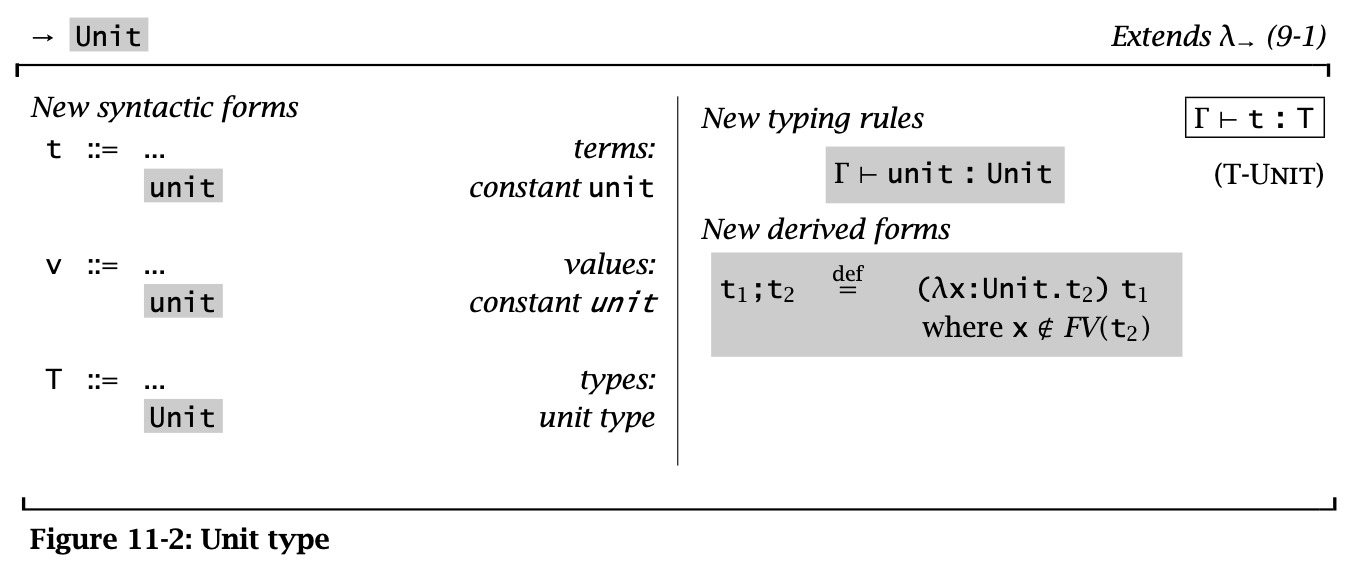
Figure 2: Unit Type

Figure 2: Unit Type

Unit type 在带副作用的语言中有很重要的作用。对于带副作用的操作的语句（例如赋值语句），可以用 Unit type 作为返回值。这点有点像 C/Java 里面的 void。

Derived Forms: Sequencing and Wildcards

Sequencing

在带副作用的语言中，语句必须要按照特定的顺序来执行。

(Sequencing notation)

\(t_1; t_2\) 可以用来表示先执行 \(t_1\)，完成后再执行 \(t_2\)。

Sequencing 有两种形式化的定义：

  • 定义一条 syntax 规则，两条 evaluation 规则

    • Evaluation rules

      \[ \frac{t_1 \rightarrow t_1’}{t_1 ; t_2 \rightarrow t_1’ ; t_2} \tag{E-Seq} \]

      \[ \operatorname{\mathtt{unit}} ; t_2 \rightarrow t_2 \tag{E-SeqNext} \]

    • Typing rule

      \[ \frac{\Gamma \vdash t_1 : \operatorname{\mathtt{Unit}} \quad \Gamma \vdash t_2 : T_2}{\Gamma \vdash t_1 ; t_2 : T_2} \tag{T-Seq} \]

  • Derived form

    \[ t_1 ; t_2 \overset{\text{def}}{=} (\lambda x : \operatorname{\mathtt{Unit}}. t_2)\ t_1 \]

    其中 \(x\) 是一个 fresh variable（即 \(x\) 不在 \(t_2\) 中出现）。由于 call-by-value 的特性，\(t_1\) 先执行

下面证明前者的规则可以从后者推出。

(Sequencing is a derived form)

记 \(\lambda^E\) 为带 Unit type、E-Seq、E-SeqNext 与 T-Seq 的语言；记 \(\lambda^I\) 为只带 Unit type 的 STLC。

令 \(e : \lambda^E -> \lambda^I\) 是一个将表达式中的 \(t_1 ; t_2\) 转换为 \((\lambda x : \operatorname{\mathtt{Unit}}. t_2)\ t_1\) 的函数，其中 \(x\) 是一个自由变量。

对于 \(t \in \lambda^E\)，有

  • \(t \rightarrow_E t’\) iff \(e(t) \rightarrow_I e(t’)\)
  • \(\Gamma \vdash^E t : T\) iff \(\Gamma \vdash^I e(t) : T\)

由于 sequencing 的规则可以被导出，所以我们只需要增加 external language 的复杂度，而不增加 internal language 的复杂度，这样使得其相关的定理证明和类型安全证明可以更加简单。这样的 derived forms 被称为语法糖（syntax sugar）。

Wildcard

另一种有用的 derived form 是 wildcard。即如果某个 abstraction 的参数没有用的话，就没必要为其取一个名字，直接用占位符（wildcard binder）_ 代替。

  • Rules for wildcard

    • Evaluation rule

      \[ (\lambda \_ : T_{11}. t_{12})\ v_2 \rightarrow t_{12} \tag{E-WildCard} \]

    • Typing rule

      \[ \frac{\Gamma \vdash t_2 : T_2}{\Gamma \vdash \lambda \_: T_1. t_2 : T_2} \]

  • Derived form

    \[ \lambda \_ : S . t \overset{\text{def}}{=} \lambda x : S. t \]

    其中 \(x\) 是一个 fresh variable。

Ascription

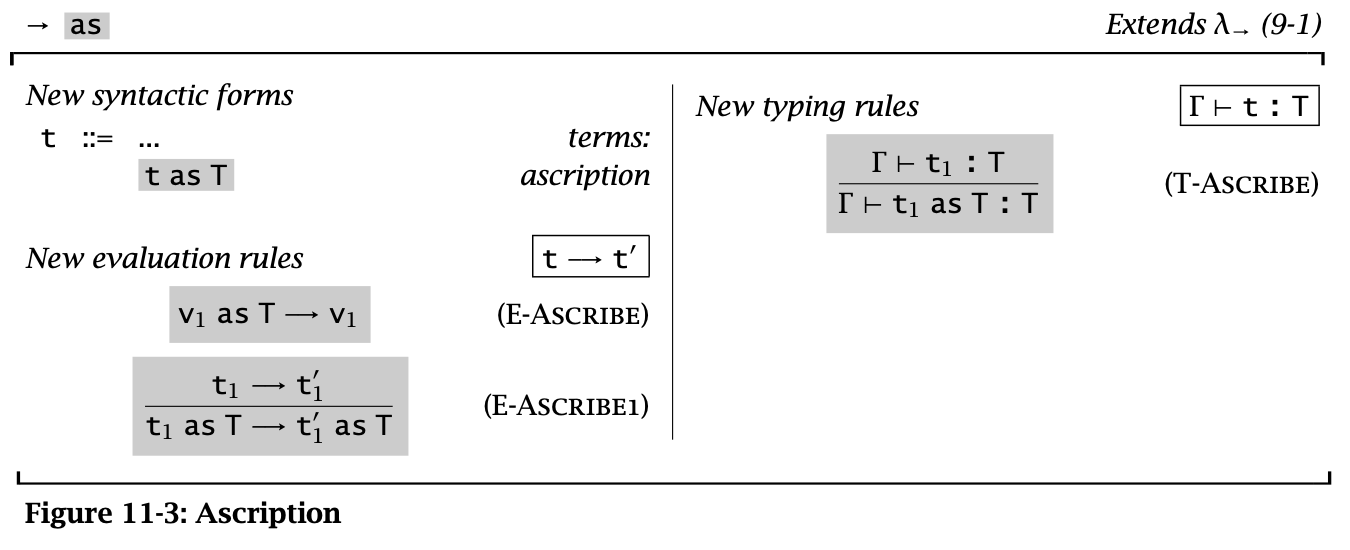
Figure 3: Ascription

Figure 3: Ascription

Ascription 不会进行任何额外的运算，而会在化简后直接返回原来的值，因此只用来标记类型。

Ascription 可以用来当作 typing assertions 或者 verifications，如果不成立会被 typechecker 报警。

除此之外，它也可以用作：

  • documentation
  • 控制类型打印：如果定义了缩写，那么 typechecker 打印类型的时候会尽量使用缩写，但是有时候 typechecker 不能识别出缩写（或者因为其他原因不用缩写），可以用 ascription 声明类型，如 \((\lambda f : \operatorname{\mathtt{Unit}} \rightarrow \operatorname{\mathtt{Unit}}. f)\ \operatorname{\mathtt{as}}\ \operatorname{\mathtt{UU}} \rightarrow \operatorname{\mathtt{UU}};\)
  • 在 subtyping 声明类型

Ascription 也是一种 derived form：

\[ t \operatorname{\mathtt{as}} T \overset{\text{def}}{=} (\lambda x : T. x)\ t \]

这里使用 call-by-value 的特性来实现 evaluation 的效果。

AscribeEager

注意，如果在 E-Ascribe 中不要求只有 value 能丢掉 ascription，也就是使用下面的 E-AscribeEager 作为 evaluation rule，那么就不能直接将 term 当作参数传入 abstraction 了：

\[ t_1 \operatorname{\mathtt{as}} T \rightarrow t_1 \tag{E-AscribeEager} \]

因为根据 call-by-value 的原则，\(t_1\) 在被替换时一定是一个 value，而这条规则并没有要求这一点。

此时 derived form 需要改成：

\[ t \operatorname{\mathtt{as}} T \overset{\text{def}}{=} (\lambda x : \operatorname{(\mathtt{Unit}} \rightarrow T). x\ \operatorname{\mathtt{unit}})\ (\lambda y : \operatorname{\mathtt{Unit}}. t) \quad \text{where $y$ is fresh in $t$} \]

这里使用了 abstraction 阻止自动求值。

这个 derived form 和原来的唯一的区别是 E-AscribeEager 求值只经过了一步，而这里需要两步进行 evaluation。这个也在意料之中，因为 sugering 本来就是为了简化语法的，那么 desugaring 也就有可能增加求值步骤。

要满足前面 derived forms 的条件的话，只要将原条件改成以下形式：

\[t \rightarrow_E t’ \quad \text{iff} \quad e(t) \rightarrow^*_I e(t’)\]

并且有

\[ \operatorname{if} e(t) \rightarrow_I s, \operatorname{then} s \rightarrow^* e(t’) \operatorname{with} t \rightarrow_E t' \]

Let Bindings

let 可以把一个表达式绑定到一个名字上。例如 \(\operatorname{\mathtt{let}} x = t_1 \operatorname{\mathtt{in}} t_2\) 表示将 \(x\) 绑定到 \(t_1\) 并且用来求值 \(t_2\)。其中 \(t_1\) 是 let-bound term，\(t_2\) 是 let-body。

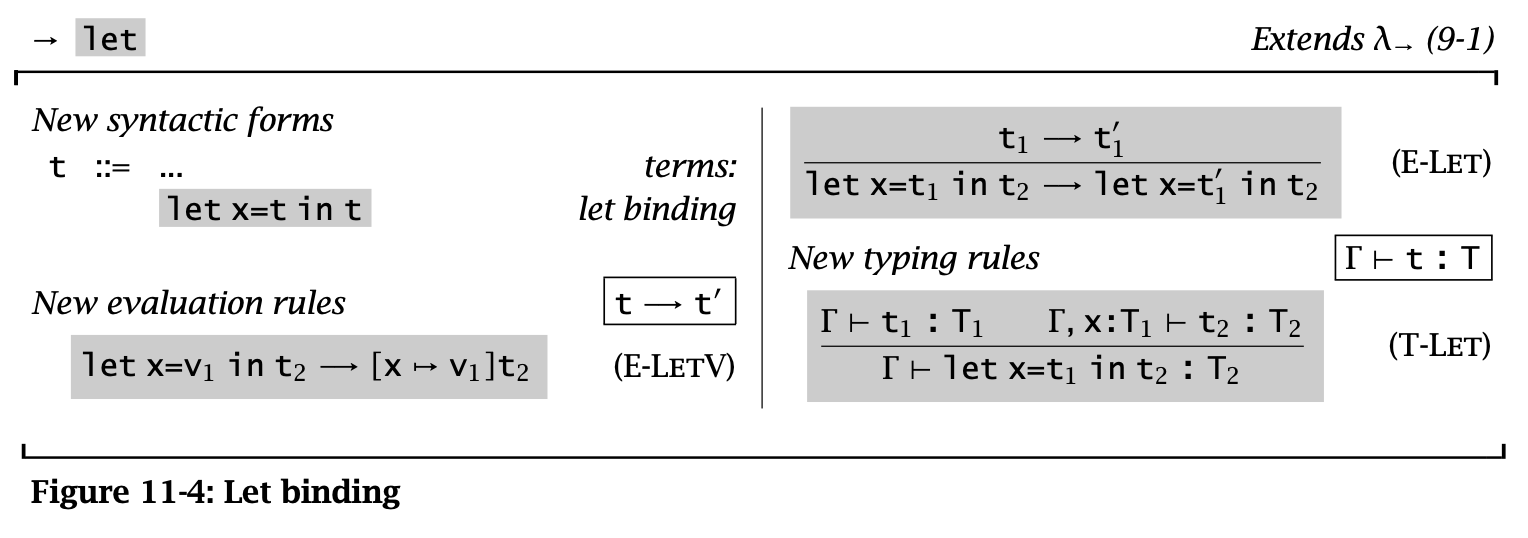
Figure 4: Let Binding

Figure 4: Let Binding

let 使用 call-by-value 的策略，即 let-bound term 必须先求值，然后才能对 let-body 进行求值。

let 也可以定义成一个 derived form：

\[ \operatorname{\mathtt{let}} x = t_1 \operatorname{\mathtt{in}} t_2 \overset{\text{def}}{=} (\lambda x : T_1 . t_2)\ t_1 \]

注意到定义左边的 let 中并没有 \(t_1\) 的类型信息，而右边 desurgared 的形式却包含了 \(x : T_1\)，说明如果要将 let 转换成 internal language，那么必须推导出它的类型信息。即展开 let 的过程不能看成对于 term 的 desurgaring 变换，而应该看作是在 typing derivation 上的变换。

\[ \frac{ \frac{\vdots}{\Gamma \vdash t_1 : T_1} \quad \frac{\vdots}{\Gamma, x : T_1 \vdash t_2 : T_2} } { \Gamma \vdash \operatorname{\mathtt{let}} x = t_1 \operatorname{\mathtt{in}} t_2 : T_2 } \text{(T-Let)} \rightarrow \frac{ \frac{ \frac{\vdots}{\Gamma, x : T_1 \vdash t_2 : T_2} }{ \Gamma \vdash \lambda x : T_1. t_2 : T_1 \rightarrow T_2 } \text{(T-Abs)} \quad \frac{\vdots}{\Gamma \vdash t_1 : T_1} } { \Gamma \vdash (\lambda x : T_1. t_2)\ t_1 : T_2 } \text{(T-App)} \]

由此可见 let-bindings 是一种比较特殊的 derived form。

能否将 let-bindings 的 derived form 定义为

\[ \operatorname{\mathtt{let}} x = t_1 \operatorname{\mathtt{in}} t_2 \overset{\text{def}}{=} [x \mapsto t_1] t_2 \]

不可以。主要的问题在于这个定义无法排除掉一些 ill-typeness：

\[ \operatorname{\mathtt{let}} x = \operatorname{\mathtt{unit}}(\operatorname{\mathtt{unit}}) \operatorname{\mathtt{in}} \operatorname{\mathtt{unit}} \rightarrow [x \mapsto \operatorname{\mathtt{unit}}(\operatorname{\mathtt{unit}})] \operatorname{\mathtt{unit}} \]

左边的 let-binding 显然是 ill-typed，但是右边由于 \(\operatorname{\mathtt{unit}}\) 中不存在 \(x\)，导致类型系统会接受这个 term，导致错误。

Product types

Pairs

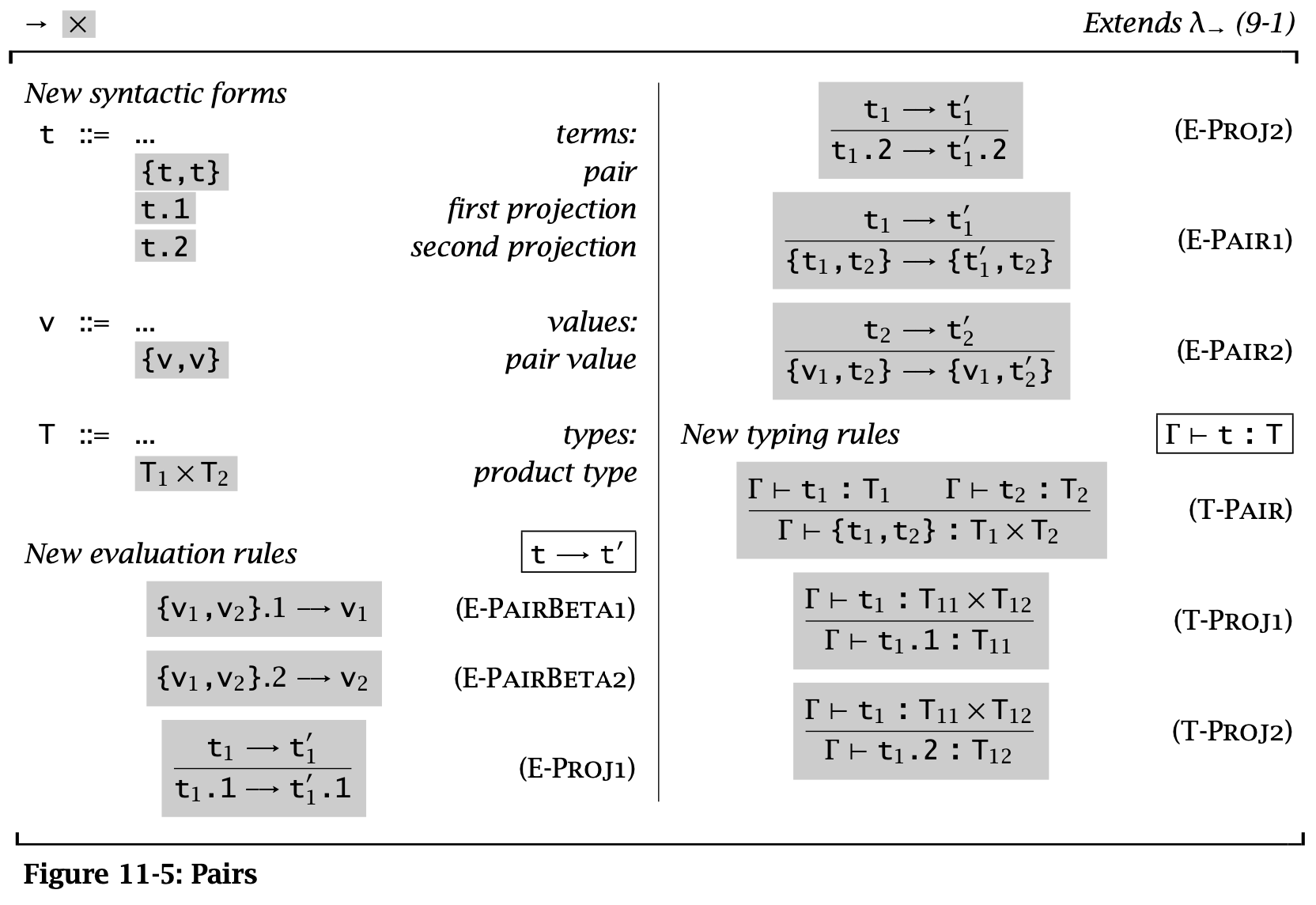
Figure 5: Pairs

Figure 5: Pairs

Pairs 是一种新的类型，记作 \(T_1 \times T_2\)，称为 product type 或者 cartesian product。 这里将 pairs 用花括号包裹，实际上一般圆括号用得比较多一些。

使用 Pairs 时，t.1 这样的操作称之为 projections。

E-PairBeta 说明了一个 full-evaluated pair 如何进行 projection 操作，E-Proj 定义了在 projections 运算中的 pair 求值的规则。

Pairs 的规则使得其强制从左到右进行求值（E-Pair2），同时只有求值后才能提取其中的元素（E-PairBeta）。同时，由于一个 pair value 中的两个元素必须都是 value，这使得在必须传递 value 的时候（比如 call by value）保证 pair 的两个元素都一定已经被求值了。

Tuples

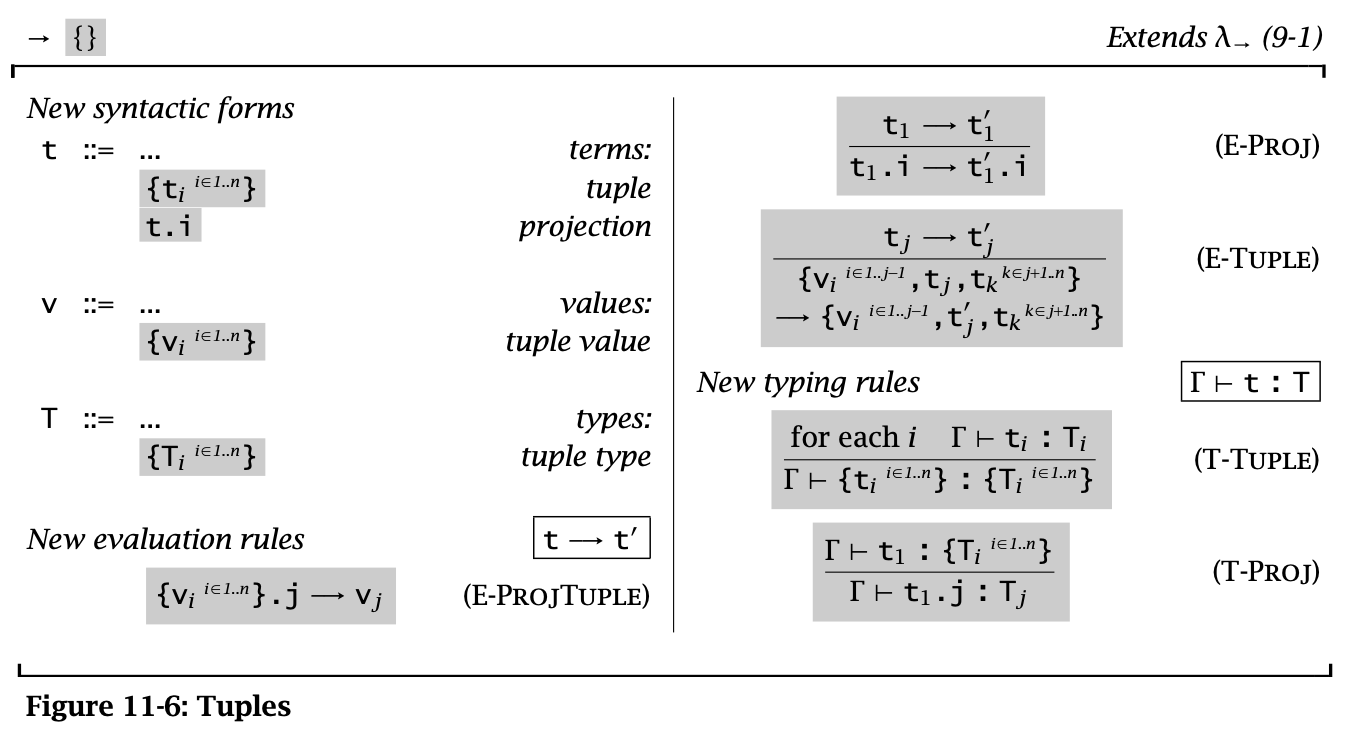
Figure 6: Tuples

Figure 6: Tuples

Tuples 是 \(n\) 元的 Pairs，其中 \(n\) 可以是 \(0\)，此时 tuple 为 \(\{\}\)。（这里还用了 \(\{v_i^{i \in 1 \dots n}\}.j \rightarrow v_j\)）

Tuple 比较特殊的一条规则是 E-Tuple，可以看成是 E-Pair 的拓展形式。

注意 tuples 也是强制从左到右求值的。

Records

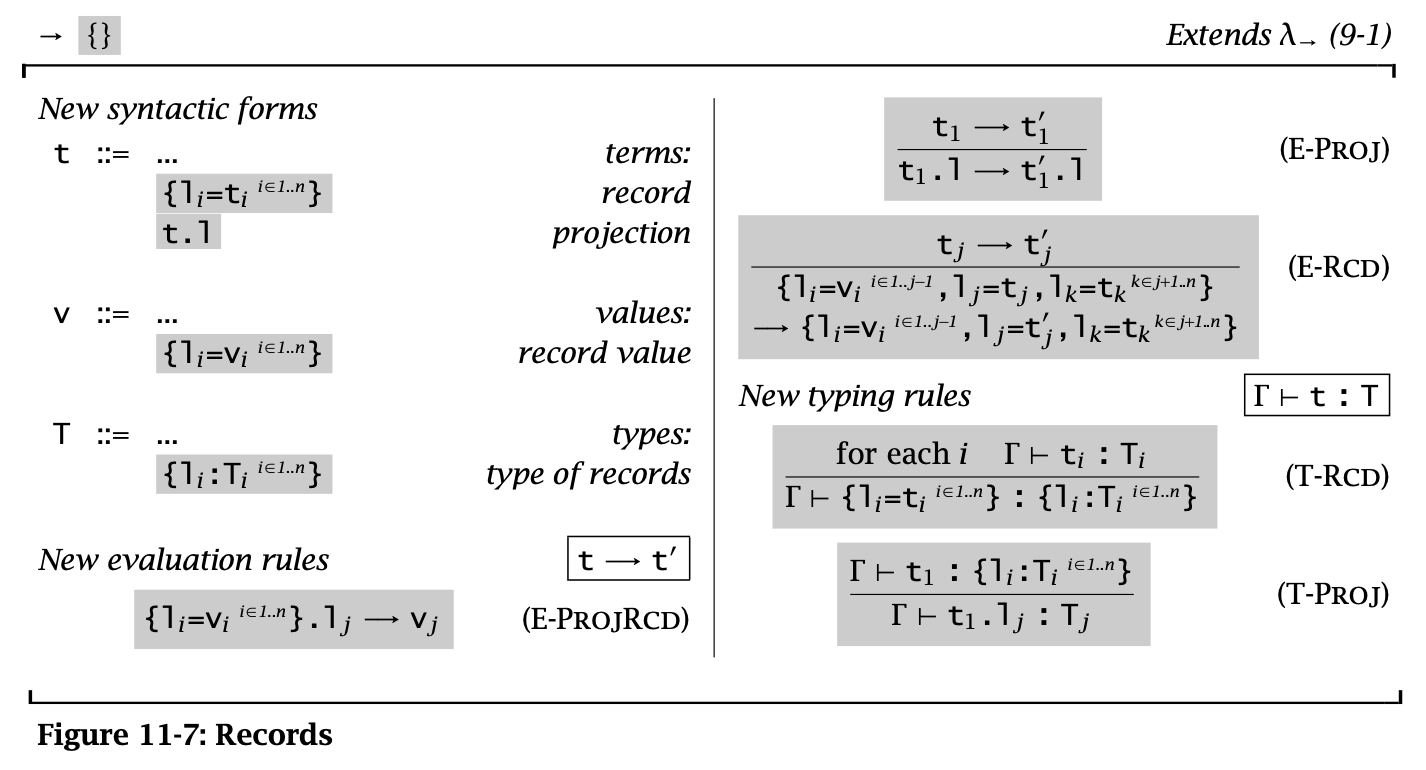
Figure 7: Records

Figure 7: Records

Records 就是加上了 label 的 tuples，其中要求所有的 label 都不相同。这个有点像 struct。

可以将 tuples 看作 label 是被省略的正整数的 records，将 pairs 看作特殊的 tuples。但是很多语言将 records 和 tuples 区分开来，因为二者在编译器中的实现不一样。

在很多语言中，records 中元素的顺序并不影响类型相等的判断，例如 \(\{a : \operatorname{\mathtt{Nat}}, b : \operatorname{\mathtt{Float}}\} = \{b : \operatorname{\mathtt{Float}}, a : \operatorname{\mathtt{Nat}}\}\)。但是这里认为二者不同，并且会认为它们拥有不同的类型。但是第十五章中，通过 subtype relation 可以认为二者相同。（是否忽视 ordering 会对编译器的性能造成很大影响，所以这里先讲 ordering records）

Pattern matching

前面介绍的 records 用了 projection 操作来提取内部的值，但是很多语言都支持使用 pattern matching 来完成这个操作。

这里通过引入 pattern syntax 来将 pattern matching 引入无类型 λ 演算。其中 pattern 可以是嵌套的，从而从嵌套的结构中提取数据。

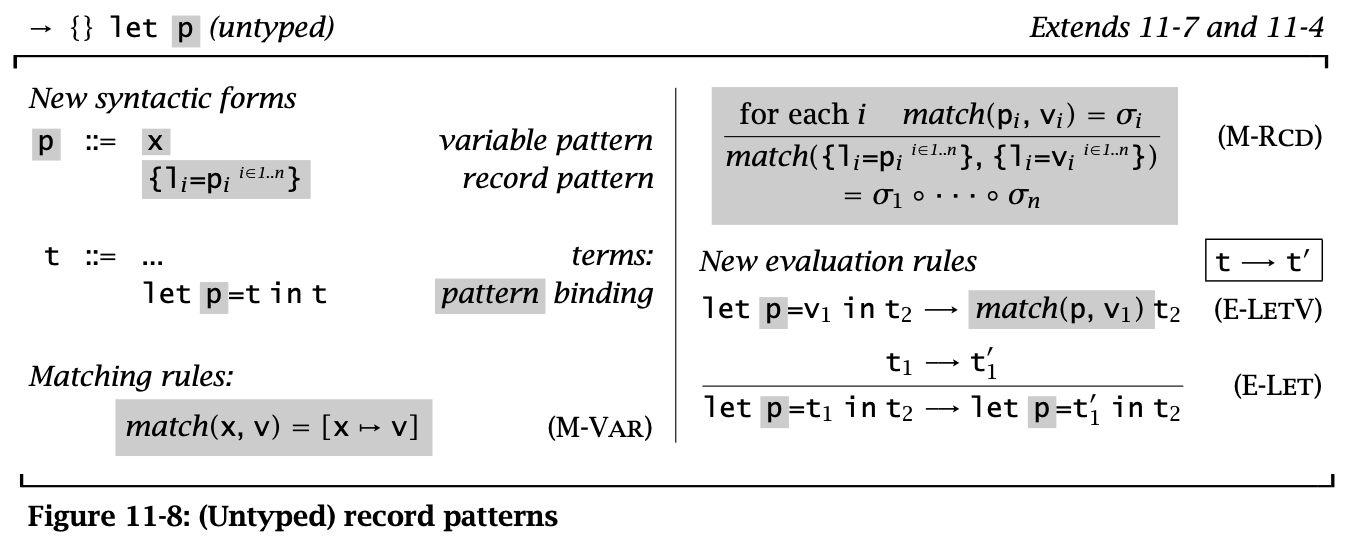
Figure 8: (Untyped) record patterns

Figure 8: (Untyped) record patterns

Pattern Matching 可以看作是一个泛化的 let-binding 规则。其依赖于一个 match(p, v) 函数，表示 value 是否与模式匹配，如果匹配就产生一个 substitution。

下面是一些 pattern matching 相关的例子：

  • \(\operatorname{\mathtt{match}}(\{x,y\}, \{5,\operatorname{\mathtt{true}}\}) \Rightarrow [x \mapsto 5, y \mapsto \operatorname{\mathtt{true}}]\)
  • \(\operatorname{\mathtt{match}}(x, \{5,\operatorname{\mathtt{true}}\}) \Rightarrow [x \mapsto \{5,\operatorname{\mathtt{true}}\}]\)
  • \(\operatorname{\mathtt{match}}(\{x\}, \{5, \operatorname{\mathtt{true}}\}) \Rightarrow \operatorname{\mathtt{fails}}\)

match 由 M-Var 和 M-Rcd 两条规则定义。前者表示一个 variable 可以和任何 value 匹配并返回一个匹配，后者定义了 record 形式下的模式匹配（这里要求 pattern 中所有的变量 \(p_i\) 都是不同的）。

下面为其加上类型：

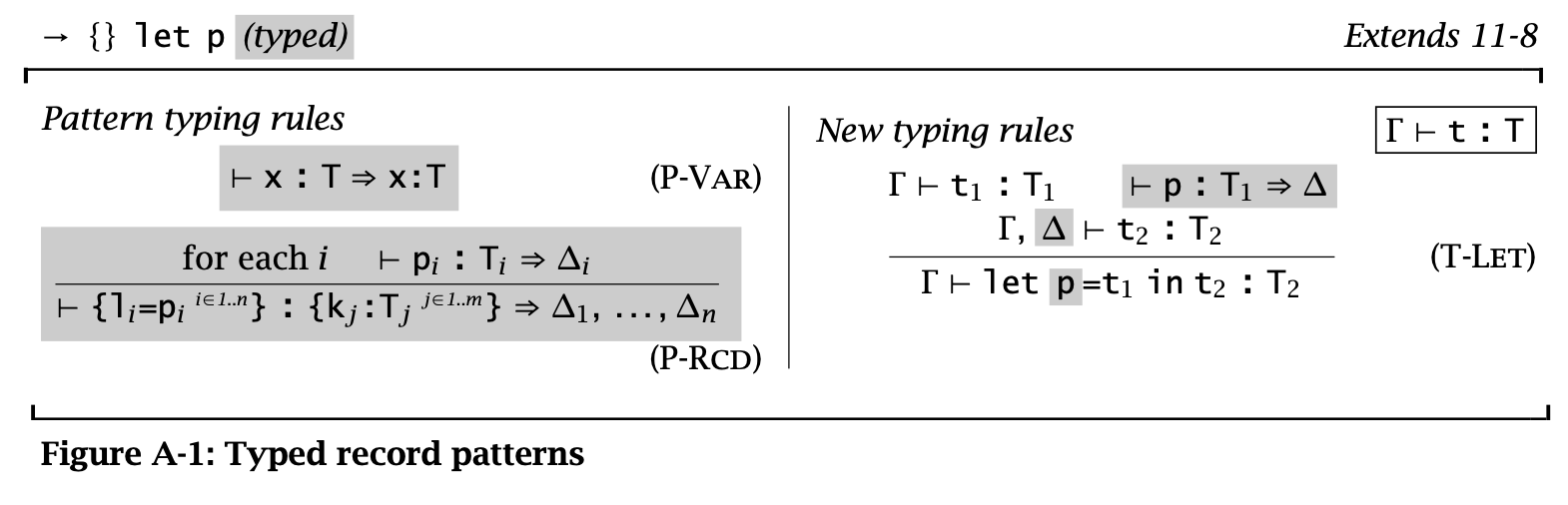
Figure 9: typed-record-patterns

Figure 9: typed-record-patterns

Pattern typing rules 中的 P-Var 首先定义了变量和其 pattern 具有相同的类型；P-Rcd 定义了 record 类型可以产生一串的 context，这些 context 包含了为 pattern 中变量提供的 bindings；后面的 T-Let 定义了如果一个 pattern 可以成功匹配时会返回一个 context \(\Delta\)，那么在类型推导时可以将这个 context 加入 \(\Gamma\) 来推导类型。

可以继续改进 record pattern typing rule，使得当 record pattern 中 fields 的数量小于 record value 中 fields 的数量时（此时只匹配 pattern 中存在的情况）仍然能继续匹配：

\[ \frac { \{ l_i^{i \in 1 \dots n} \} \in \{ k_j^{j \in 1 \dots m} \} \qquad \forall{i \in 1 \dots n}. \exist{j \in 1 \dots m}. l_i = k_j \operatorname{\mathtt{and}} \vdash p_i : T_j \Rightarrow \Delta_i } { \vdash \{ l_i = p_i^{i \in 1 \dots n} \} : \{ k_j : T_j^{j \in 1 \dots m} \} \Rightarrow \Delta_1, \dots, \Delta_n } \tag{P-Rcd’} \]

如果加入了这条规则，那么就可以将 Record 类型的 projection 规则从初始规则中删去，并将其看作一个语法糖：

\[ t.l \overset{\text{def}}{=} \operatorname{\mathtt{let}} \{ l = x \} = t \operatorname{\mathtt{in}} x \]

这个系统的 Preservation 需要用到下面两个 lemmas：

设 \(\sigma\) 是一个 substitution，\(\Delta\) 是一个 context，且 \(\Delta\) 与 \(\sigma\) 定义域相同，那么 \(\Gamma \vdash \sigma \vDash \Delta\) 表示 \(\forall x \in dom(\Delta), \Gamma \vdash \sigma(x) : \Delta(x)\)

If \(\Gamma \vdash t:T\) and \(\vdash p : T \Rightarrow \Delta\), then \(\operatorname{\mathtt{match}}(p, t) = \sigma\), with \(\Gamma \vdash \sigma \vDash \Delta\).

(Generalized substitution lemma)

\(\Gamma, \Delta \vdash t : T\) and \(\Gamma \vdash \sigma \vDash \Delta\), then \(\Gamma \vdash \sigma t : T\).

Sum types

Sums

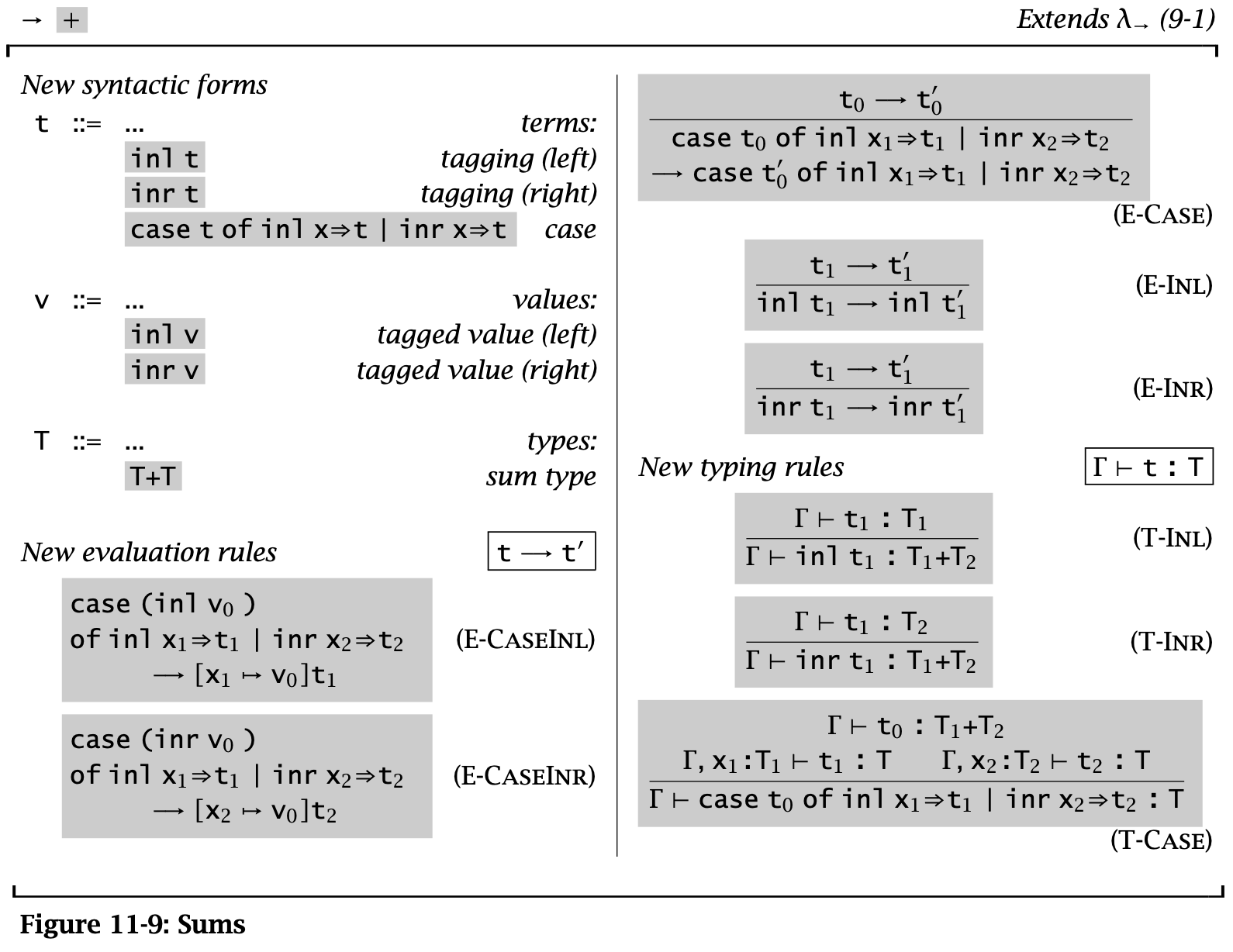
Figure 10: Sums without unique typing

Figure 10: Sums without unique typing

Sums 是一种二元的 Variants 类型。一个 Sums 类型可以包含两种类型，用 inl 与 inr 这两种 tag 来进行区分。例如若 \(a : A\)，则 \(\operatorname{\mathtt{inl}} a : A + B\)。

不难发现 inl 和 inr 可以看作是两个函数（实际上并不是函数）：

\[ \operatorname{\mathtt{inl}} : A \rightarrow A + B \]

\[ \operatorname{\mathtt{inr}} : B \rightarrow A + B \]

使用 sums 类型时可以用 case 来提取值，Sums 中不同的类型会匹配到不同的分支：

\begin{alignat*}{3} \operatorname{\mathtt{getName}} ={}& \lambda a : A + B.&&&& \\ {}& \qquad \ \ \operatorname{\mathtt{case}}&& a \operatorname{\mathtt{of}}&& \\ {}& \qquad \qquad && \operatorname{\mathtt{inl}}\ x &{} \Rightarrow {}& x \\ {}& \qquad \qquad | && \operatorname{\mathtt{inr}}\ y &{} \Rightarrow {}& y; \end{alignat*}

值得注意的是在 T-Case 规则中要求 case 的结果的类型是唯一的。另外这里虽然没指出 \(x_i\) 的 scope 是 \(t_i\)，但是这一点可以从条件中得到。

if 可以看作是特殊的 case：

\begin{alignat*}{2} & \operatorname{\mathtt{Bool}} &&\overset{\text{def}}{=} \operatorname{\mathtt{Unit}} + \operatorname{\mathtt{Unit}} \\ & \operatorname{\mathtt{true}} &&\overset{\text{def}}{=} \operatorname{\mathtt{inl}}\ \operatorname{\mathtt{unit}} \\ & \operatorname{\mathtt{false}} &&\overset{\text{def}}{=} \operatorname{\mathtt{inr}}\ \operatorname{\mathtt{unit}} \\ & \operatorname{\mathtt{if}}\ t_0\ \operatorname{\mathtt{then}}\ t_1\ \operatorname{\mathtt{else}}\ t_2 &&\overset{\text{def}}{=} \operatorname{\mathtt{case}}\ t_0\ \operatorname{\mathtt{of}}\ \operatorname{\mathtt{inl}}\ x_1 \Rightarrow t_1 \mid \operatorname{\mathtt{inr}}\ x_2 \Rightarrow t_2 \\ &&& \qquad \text{where $x_1$ and $x_2$ are fresh} \end{alignat*}

Sums and Uniqueness of Types

大多数在 pure \(\lambda_\rightarrow\) 中的定理在 Sums 中都成立，除了 Uniqueness of Types theorem。因为假设 \(a : A\)，则 \(\forall B. \operatorname{\mathtt{inl}} a : A + B\) 可能表示无数的类型。Uniqueness theorem 不成立导致类型检查变得更麻烦了，因为没办法和之前一样“自底向上地使用规则检查”。此时有两种解决方案：

  • 从后面的程序里面推测 \(T\) 的类型（type reconstruction）
  • 允许 \(T\) 表示所有可能的类型（subtyping）
  • 要求手动提供类型（此处暂时采用的方案）

这里使用第三种方案，添加了一些扩展要求指明类型（有点像 ascription，但是这些是语法要求不能删去的）：

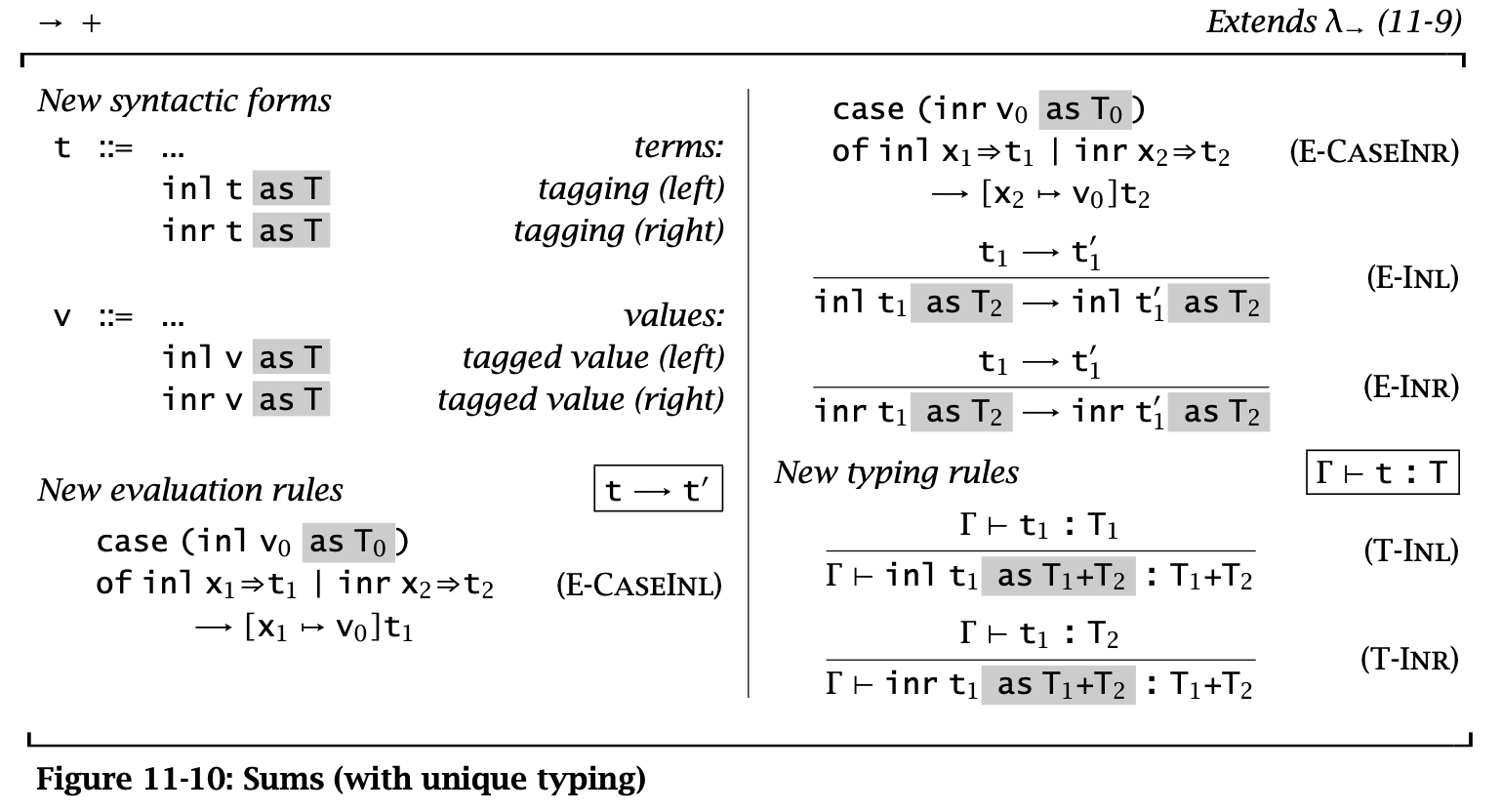
Figure 11: Sums with unique typing

Figure 11: Sums with unique typing

Variants

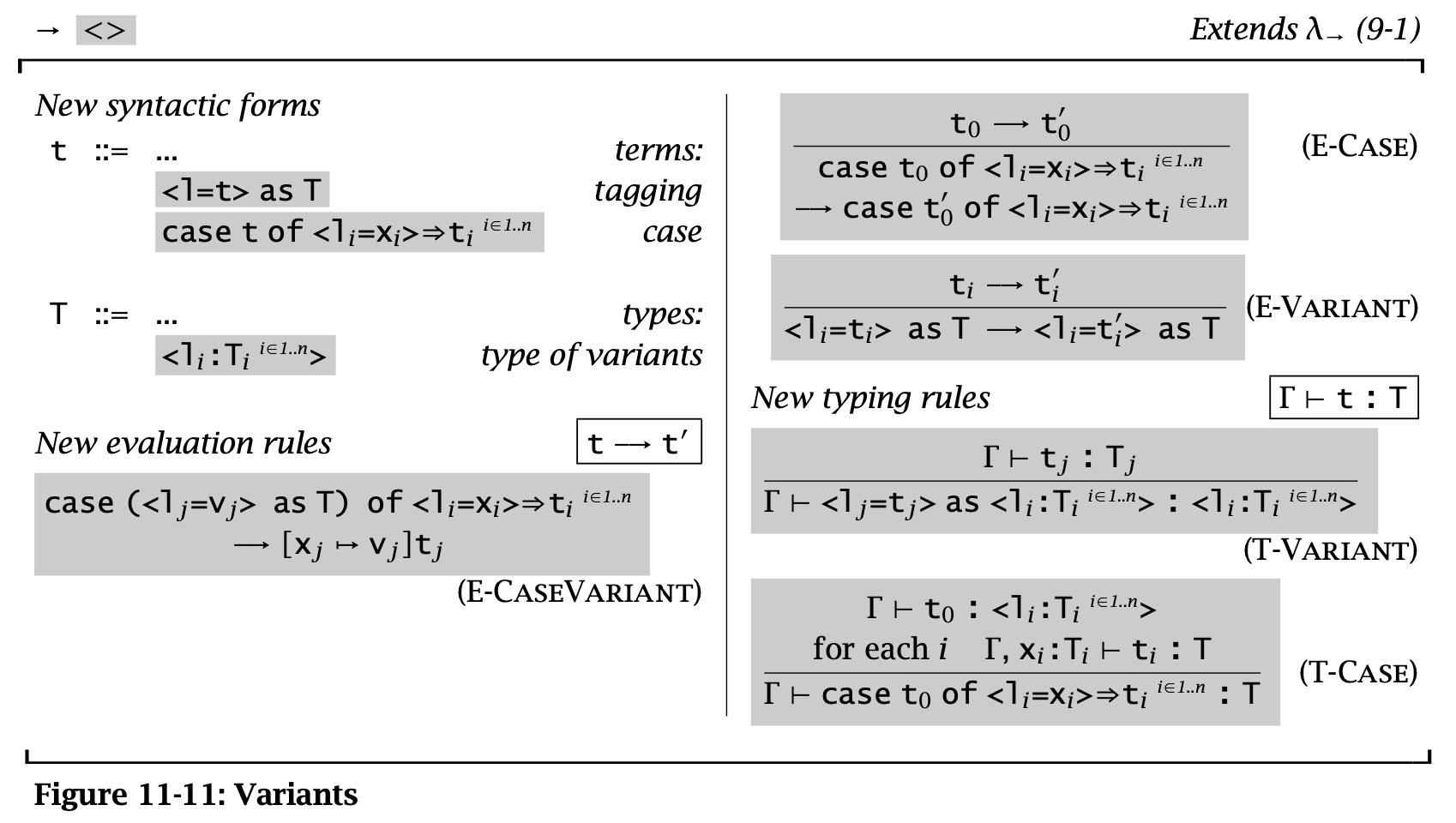
Figure 12: 11-11 Variants

Figure 12: 11-11 Variants

上面漏了一条 value syntax：

\begin{aligned} v \Coloneqq & \dots \\ & \langle l = v \rangle \operatorname{\mathtt{as}} T \\ \end{aligned}

Variants 是二元 Sums 类型的泛化，和 Records 一样有 labels。Sums 中的 \(\operatorname{\mathtt{inl}} t \operatorname{\mathtt{as}} T_1 + T_2\) 写成 \(\langle l_1=t\rangle \operatorname{\mathtt{as}} \langle l_1 : T_1, l_2 : T_2\rangle\)。

需要注意的是 Variants 和 Records 一样，标签的顺序不同则类型也不同。

Options

Options 是很常见的一种 Variants：

\[ \operatorname{\mathtt{OptionalNat}} = \langle\operatorname{\mathtt{none}} : \operatorname{\mathtt{Unit}}, \operatorname{\mathtt{some}} : \operatorname{\mathtt{Nat}}\rangle; \]

例如使用 Options 构建一个 table：

\begin{alignat*}{2} & \operatorname{\mathtt{Table}} &&= \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{OptionalNat}}; \\ & \operatorname{\mathtt{emptyTable}} &&= \lambda n : \operatorname{\mathtt{Nat}}. \langle\operatorname{\mathtt{none}} = \operatorname{\mathtt{unit}}\rangle \operatorname{\mathtt{as}} \operatorname{\mathtt{OptionalNat}}; \\ & \operatorname{\mathtt{extendTable}} &&= \lambda t : \operatorname{\mathtt{Table}}. \lambda m : \operatorname{\mathtt{Nat}}. \lambda v : \operatorname{\mathtt{Nat}}. \\ &&& \qquad \lambda n : \operatorname{\mathtt{Nat}}. \\ &&& \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{equal}}\ n\ m\ \operatorname{\mathtt{then}}\ \langle\operatorname{\mathtt{some}} = v\rangle\ \operatorname{\mathtt{as}} \operatorname{\mathtt{OptionalNat}}; \\ &&& \qquad \qquad \operatorname{\mathtt{else}}\ t\ n; \end{alignat*}

注意，\(\operatorname{\mathtt{extendTable}}\) 的类型为 \(\operatorname{\mathtt{Table}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Table}}\)。

此时就可以使用 \(x = t(5)\) 的方式来在 table 中查询值。

C/C++/Java 中允许指针（其实是一种 Reference Type）的值为 null，这实际上也是一种 Options 类型，其实际类型为 \(\operatorname{\mathtt{Ref}}(\operatorname{\mathtt{Option}}(T))\)。

Enumerations

Enumerations（Enumerated Type）是一种退化了的 Variants 类型，其 fields 值均为 Unit。例如：

\[ \operatorname{\mathtt{Bool}} = \langle\operatorname{\mathtt{true}} : \operatorname{\mathtt{Unit}}, \operatorname{\mathtt{false}} : \operatorname{\mathtt{Unit}}\rangle; \]

由于 enumerations 中的值均为 Unit，因此在 enumeration 中可以用 case 实现运算：

\begin{alignat*}{3} \operatorname{\mathtt{negative}} ={}& \lambda b : \operatorname{\mathtt{Bool}}.&&&& \\ {}& \qquad \operatorname{\mathtt{case}}&& b \operatorname{\mathtt{of}}&& \\ {}& \qquad \qquad &&\langle\operatorname{\mathtt{true}} = x\rangle & \Rightarrow & \langle\operatorname{\mathtt{false}} = x\rangle \operatorname{\mathtt{as}} \operatorname{\mathtt{Bool}} \\ {}& \qquad \qquad | &&\langle\operatorname{\mathtt{false}} = x\rangle & \Rightarrow & \langle\operatorname{\mathtt{true}} = x\rangle \operatorname{\mathtt{as}} \operatorname{\mathtt{Bool}}; \end{alignat*}

Single-Field Variants

Variants 的另一种退化形式是 Single-Field Variants（例如 newtype），即只有一个 label 的情况：

\[ V = \langle l : T\rangle; \]

这个看起来好像用处不大，因为它只有一个 label，而且在 \(\langle l = t \rangle\) 中所有对 \(t\) 的操作都要先 unpackaging 后才能进行，但是这个特性却能够防止出现一些类型错误。

例如写了一个将美元转换成欧元的函数 \(\operatorname{\mathtt{dollars2euros}}\)，则可能会出现这样的错误转换：

\[ \operatorname{\mathtt{dollars2euros}}\ (\operatorname{\mathtt{dollars2euros}}\ \operatorname{\mathtt{mybankbalance}}) \]

但是如果用 Single-Field Variants 来定义，当写出类似的错误程序时就能通过类型检查出来：

\begin{alignat*}{2} & \operatorname{\mathtt{DollarAmount}} &&={} \langle\operatorname{\mathtt{dollars}} : \operatorname{\mathtt{Float}}\rangle; \\ & \operatorname{\mathtt{EuroAmount}} &&={} \langle\operatorname{\mathtt{euros}} : \operatorname{\mathtt{Float}}\rangle; \\ & \operatorname{\mathtt{dollars2euros}} &&={} \lambda d : \operatorname{\mathtt{DollarAmount}}. \\ & && \qquad \operatorname{\mathtt{case}} d \operatorname{\mathtt{of}} \\ & && \qquad \qquad \langle\operatorname{\mathtt{dollars}} = \operatorname{\mathtt{x}}\rangle \Rightarrow \langle\operatorname{\mathtt{euros}} = \operatorname{\mathtt{timesfloat}}\ x\ 1.1325\rangle \operatorname{\mathtt{as}} \operatorname{\mathtt{EuroAmount}}; \end{alignat*}

Variants vs Datatypes

Variants \(\langle l_i : T_i^{i \in 1 \dots n} \rangle\) 和 ML 里面的 Datatypes 有点像：

\begin{alignat*}{2} \operatorname{\mathtt{type}} T = {}&l_1 \operatorname{\mathtt{of}} T_1 \\ |\ &l_2 \operatorname{\mathtt{of}} T_2 \\ |\ &\dots \\ |\ &l_n \operatorname{\mathtt{of}} T_n; \end{alignat*}

但是二者之间有很多区别：

  1. 一个 trivial 的区别就是在 OCaml 中，类型必须以小写字母开头，datatypes 的 constructors 必须以大写字母开头。当然这本书里面不会这么区别，不过按照 OCaml 的写法上面的 Datatype 应该要写成 \[\operatorname{\mathtt{type}}\ t = L_i \operatorname{\mathtt{of}} T_i^{i \in 1 \dots n}\]
  2. OCaml 中的 datatypes 不需要额外的类型标注，因为 datatypes 必须先声明再使用，并且在作用域内其 labels 的名称是唯一的，因此只需要 label 就可以推断出类型（Variants 则必须要标注）；
  3. OCaml 中如果 datatype 的 associated type 是 unit type，那么就可以省略不写，如 \[\operatorname{\mathtt{type}}\ \operatorname{\mathtt{Bool}} = \operatorname{\mathtt{true}} \| \operatorname{\mathtt{false}};\]
  4. OCaml 中的 datatypes 不仅包含了 variants 的特性，还有 recursive types 的特性（如 List 就是递归定义的）。并且 datatypes 还可以接受 parameters，当作 type operator 用。

Variants as Disjoint Unions

Sums 和 Variants 有时被称为 Disjoint Unions。一方面这两种类型是其他类型的“union”；另一方面这两种类型都有 tag，用不同的 tag 标注的数据互不相同，所以类型之间是不相交的（disjoint）。

现在 Union Type 一般指 untagged union（或者 non-disjoint union）。

Type Dynamic

很多静态分析都要处理动态数据（例如从数据库中读取或者跨网络传输），因此会提供用于运行时判定类型的工具。

实现这种操作的一种方式就是添加 Dynamic Type，这种 Variants 类型的 tag 为 T，value 为 v，其中 v 的类型就是 T（即将类型作为 tag 使用）。Dynamic Type 可以用 typecase 获取其中的值。

Dynamic Type 可以看作是一种 infinite disjoint union，其 tags 就是类型。

General Recursion

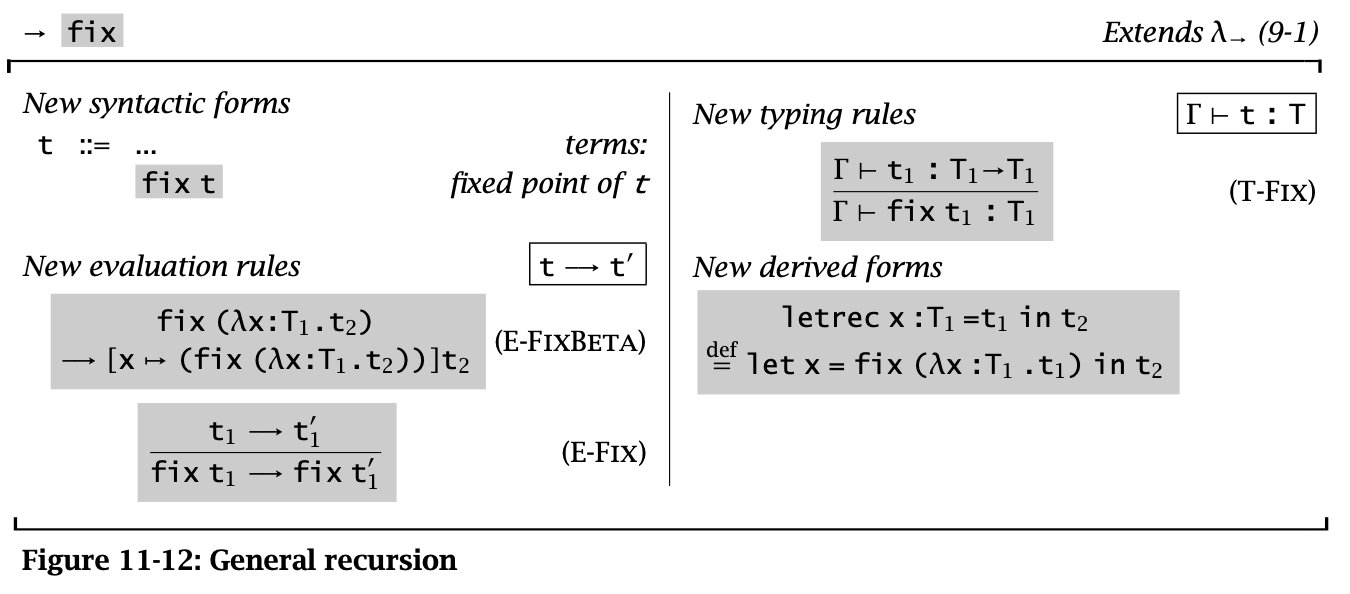
Figure 13: General Recursive

Figure 13: General Recursive

即 \(\operatorname{\mathtt{fix}}\ f = f\ (\operatorname{\mathtt{fix}}\ f)\)

在无类型 λ 演算中可以用 fix combinator 实现递归函数，但是在 STLC 中却不行，因为 fix 的类型无法在 STLC 中表达。并且无法终止的运算都无法在 simple types 描述类型。所以这里添加 typing ruls 并用 letrec 来模仿无类型 λ 演算中 fix combinator 的行为。

这种只含有数字和 fix 的 STLC 具有很多微妙的语义现象（例如 full abstraction），这样的系统被称为 PCF。

fix 一般用来构建函数，但是并没有限定函数，例如可以传入下面的 records，这样就能构造出互相调用的函数：

\begin{alignat*}{3} & \operatorname{\mathtt{ff}} = \lambda \operatorname{\mathtt{ieio}} : \{ \operatorname{\mathtt{iseven}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}}, \operatorname{\mathtt{isodd}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}}\}. \\ & \qquad \qquad \{ \operatorname{\mathtt{iseven}} = \lambda x : \operatorname{\mathtt{Nat}}. \\ & \qquad \qquad \qquad \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ x\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{true}} \\ & \qquad \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{ieio}}.\operatorname{\mathtt{isodd}}\ (\operatorname{\mathtt{pred}}\ x), \\ & \qquad \qquad \ \ \operatorname{\mathtt{isodd}} = \lambda x : \operatorname{\mathtt{Nat}}. \\ & \qquad \qquad \qquad \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ x\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}} \\ & \qquad \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{ieio}}.\operatorname{\mathtt{iseven}}\ (\operatorname{\mathtt{pred}}\ x) \}; \\ & \operatorname{\mathtt{ff}} : \{ \operatorname{\mathtt{iseven}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}}, \operatorname{\mathtt{isodd}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}} \} \rightarrow \\ & \qquad \qquad \{ \operatorname{\mathtt{iseven}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}}, \operatorname{\mathtt{isodd}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}} \} \\ & \operatorname{\mathtt{r}} = \operatorname{\mathtt{fix}}\ \operatorname{\mathtt{ff}}; \\ & \operatorname{\mathtt{r}} : \{ \operatorname{\mathtt{iseven}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}}, \operatorname{\mathtt{isodd}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}} \} \\ & \operatorname{\mathtt{r}}.\operatorname{\mathtt{iseven}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}} \end{alignat*}

除此之外，对于任何 \(T\)，fix 都可以构造出一个 \(T \rightarrow T\)，这会产生一些有趣的效果。这说明任何类型 \(T\) 都可以构造出一个类型可以被推导出来的 term。例如下面的 \(\operatorname{\mathtt{diverge}}_T\) 函数：

\begin{alignat*}{3} & \operatorname{\mathtt{diverge}}_T =&& \lambda_\_ : \operatorname{\mathtt{Unit}}. \operatorname{\mathtt{fix}}\ (\lambda x: T.x); \\ & \operatorname{\mathtt{diverge}}_T :&& \operatorname{\mathtt{Unit}} \rightarrow T \end{alignat*}

这里 \(\operatorname{\mathtt{diverge}}_T\) 的计算永远不会终止，因为每次计算都会返回相同的 term，但是其类型仍然是 \(T\)。此时称 \(\operatorname{\mathtt{diverge}}_T\ \operatorname{\mathtt{unit}}\) 是 \(T\) 的一个 undefined element。

下面是用 fix 实现 equal, plus, times, and factorial 的一些例子：

\begin{alignat*}{2} & \operatorname{\mathtt{equal}} = \\ & \qquad \operatorname{\mathtt{fix}} \\ & \qquad \qquad (\lambda \operatorname{\mathtt{eq}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}} . \\ & \qquad \qquad \qquad \lambda m : \operatorname{\mathtt{Nat}}. \lambda n : \operatorname{\mathtt{Nat}}. \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ m\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{iszero}}\ n \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ n\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}} \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{eq}}\ (\operatorname{\mathtt{pred}}\ m)\ (\operatorname{\mathtt{pred}}\ n)); \end{alignat*}

\begin{alignat*}{2} & \operatorname{\mathtt{plus}} = \\ & \qquad \operatorname{\mathtt{fix}} \\ & \qquad \qquad (\lambda \operatorname{\mathtt{p}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} . \\ & \qquad \qquad \qquad \lambda m : \operatorname{\mathtt{Nat}}. \lambda n : \operatorname{\mathtt{Nat}}. \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ m\ \operatorname{\mathtt{then}}\ n \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{succ}}\ (p\ (\operatorname{\mathtt{pred}}\ m)\ n)); \end{alignat*}

\begin{alignat*}{2} & \operatorname{\mathtt{times}} = \\ & \qquad \operatorname{\mathtt{fix}} \\ & \qquad \qquad (\lambda \operatorname{\mathtt{t}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} . \\ & \qquad \qquad \qquad \lambda m : \operatorname{\mathtt{Nat}}. \lambda n : \operatorname{\mathtt{Nat}}. \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ m\ \operatorname{\mathtt{then}}\ 0 \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{plus}}\ (t\ (\operatorname{\mathtt{pred}}\ m)\ n)); \end{alignat*}

\begin{alignat*}{2} & \operatorname{\mathtt{factorial}} = \\ & \qquad \operatorname{\mathtt{fix}} \\ & \qquad \qquad (\lambda \operatorname{\mathtt{f}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Nat}} . \\ & \qquad \qquad \qquad \lambda n : \operatorname{\mathtt{Nat}}. \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ n\ \operatorname{\mathtt{then}}\ 1 \\ & \qquad \qquad \qquad \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{times}}\ (f\ (\operatorname{\mathtt{pred}}\ n)\ n)); \end{alignat*}

letrec

在写程序时，一般会用 letrec：

\begin{alignat*}{3} & \operatorname{\mathtt{letrec}}\ \operatorname{\mathtt{iseven}} : \operatorname{\mathtt{Nat}} \rightarrow \operatorname{\mathtt{Bool}} = \\ & \quad \lambda x : \operatorname{\mathtt{Nat}}. \\ & \qquad \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ x\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{true}} \\ & \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{if}}\ \operatorname{\mathtt{iszero}}\ (\operatorname{\mathtt{pred}}\ x)\ \operatorname{\mathtt{then}}\ \operatorname{\mathtt{false}} \\ & \qquad \operatorname{\mathtt{else}}\ \operatorname{\mathtt{iseven}}\ (\operatorname{\mathtt{pred}}\ (\operatorname{\mathtt{pred}}\ x)) \\ & \operatorname{\mathtt{in}} \\ & \quad \operatorname{\mathtt{iseven}}\ 7; \end{alignat*}

letrec 也是一个 derived form：

\[ \operatorname{\mathtt{letrec}}\ x : T_1 = t_1 \operatorname{\mathtt{in}} t_2 \overset{\operatorname{\mathtt{def}}}{=} \operatorname{\mathtt{let}} x = \operatorname{\mathtt{fix}} (\lambda x : T_1 . t_1) \operatorname{\mathtt{in}} t_2 \]

List

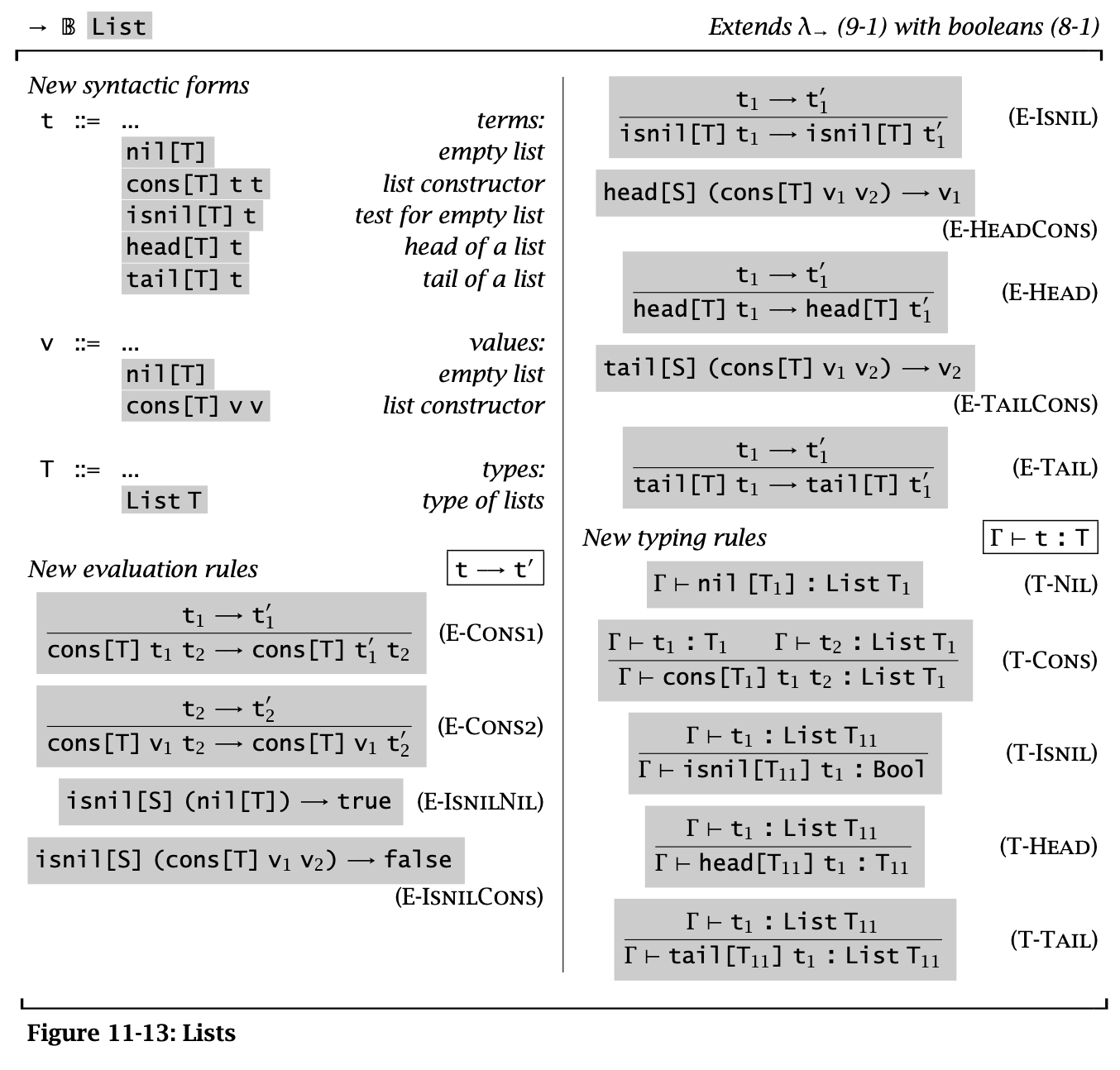
Figure 14: Lists

Figure 14: Lists

List 是一个 type constructor，空 List 记作 \(\operatorname{\mathtt{nil}}[T]\)，并且可以用 \(\operatorname{\mathtt{cons}}[T]\ t_1\ t_2\) 来构建。除此之外还有 \(\operatorname{\mathtt{head}}[T]\ t\)、\(\operatorname{\mathtt{tail}}[T]\ t\)、\(\operatorname{\mathtt{isnil}}[T]\ t\) 等函数。

大部分 lists 函数标注的类型都可以从参数里推断出来，但是 \(\operatorname{\mathtt{nil}}[T]\) 这样的就不行。

这里用 head / tail / isnil 来构建 lists，并将它们定义为 primitives，但是一般会用 datatype 和 case 去构建和使用，这样可以更容易地发现类型错误。

CATALOG