本章讨论包含 Bool 和 λ 演算的类型系统,在保证类型安全的同时,使其可以描述我们写的大多数程序。
由于纯 λ 演算是图灵完备的,所以无法准确地确定一个程序的准确类型。例如下面的程序只有在运行时才能知道具体的返回类型:
\[ \operatorname{\mathtt{if}} \langle \text{long and tricky computation} \rangle \operatorname{\mathtt{then}} \operatorname{\mathtt{true}} \operatorname{\mathtt{else}} (\lambda x. x) \]
本章实现的 STLC 记作 \(\lambda_\rightarrow\)。
Function Types
函数类型:
\[ \lambda x.t : \rightarrow \]
为了让类型描述得更准确,需要加入参数类型和返回值类型:
\[ T_1 \rightarrow T_2 \]
Type constructor \(\rightarrow\) 是右结合的,所以 \(T_1 \rightarrow T_2 \rightarrow T_3 = T_1 \rightarrow (T_2 \rightarrow T_3)\)。
注意 \((\operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Bool}}) \rightarrow \operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Bool}}\) 表示传入一个函数;而 \(\operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Bool}}\) 只是传入一个 Bool。
The set of simple types over the type Bool is generated by the following grammar:
\begin{aligned} T \Coloneqq & & \text{types} \\ & \mathtt{Bool} & \text{type of booleans} \\ & T \rightarrow T & \text{type of functions} \end{aligned}
The Typing Relation
Abstraction
Arguments
有两种方式可以给出一个 abstraction 的参数的类型(这本书主要使用 explicitly typed):
- 显式写出类型 \(\lambda x : T_1 . t_2\),这可以帮助类型检查器进行检查,称为 explicitly typed
- 让类型检查器自动推导(这个过程称为 infer 或 reconstruct),称为 implicitly typed(在 λ 演算中,也会称之为 type-assignment systems)
Body
知道了参数类型后,其函数返回值类型即为 body 的类型。
\[ \dfrac { x : T_1 \vdash t_2 : T_2 } { \vdash \lambda x : T_1 . t_2 : T_1 \rightarrow T_2 } \tag{T-Abs} \]
Typing context
当对象嵌套在一个 abstraction 里面的时候,需要考虑其所在的上下文,表示为 \(\Gamma \vdash t : T\)。其中 \(\Gamma\) 称为 typing context 或者 type environment。如果没有上下文环境,则可以记作 \(\emptyset\),或者不在类型推导中写出,即 \(\vdash t : T\)。
用逗号可以向环境中添加规则,例如 \(\Gamma, x : T_1 \vdash t_2 : T_2\)。添加规则时可能会遇到变量重名的问题,此时可以做 alpha-conversion。
\(\Gamma\) 可以看作一个将变量映射到类型的有穷函数,其定义域为被绑定的变量集合,记作 \(dom(\Gamma)\)。
\[ \dfrac { \Gamma, x : T_1 \vdash t_2 : T_2 } { \Gamma \vdash \lambda x : T_1 . t_2 : T_1 \rightarrow T_2 } \tag{T-Abs} \]
通过 \(\Gamma\) 也可以得到变量的类型:
\[ \dfrac { x : T \in \Gamma } { \Gamma \vdash x : T } \tag{T-Var} \]
Application
\[ \dfrac { \Gamma \vdash t_1 : T_{11} \rightarrow T_{12} \qquad \Gamma \vdash t_2 : T_{11} } { \Gamma \vdash t_1\ t_2 : T_{12} } \tag{T-App} \]
If
\[ \dfrac { \Gamma \vdash t_1 : \operatorname{\mathtt{Bool}} \qquad \Gamma \vdash t_2 : T \qquad \Gamma \vdash t_3 : T } { \Gamma \vdash \operatorname{\mathtt{if}} t_1 \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 : T } \tag{T-If} \]
\(\lambda_\rightarrow\)
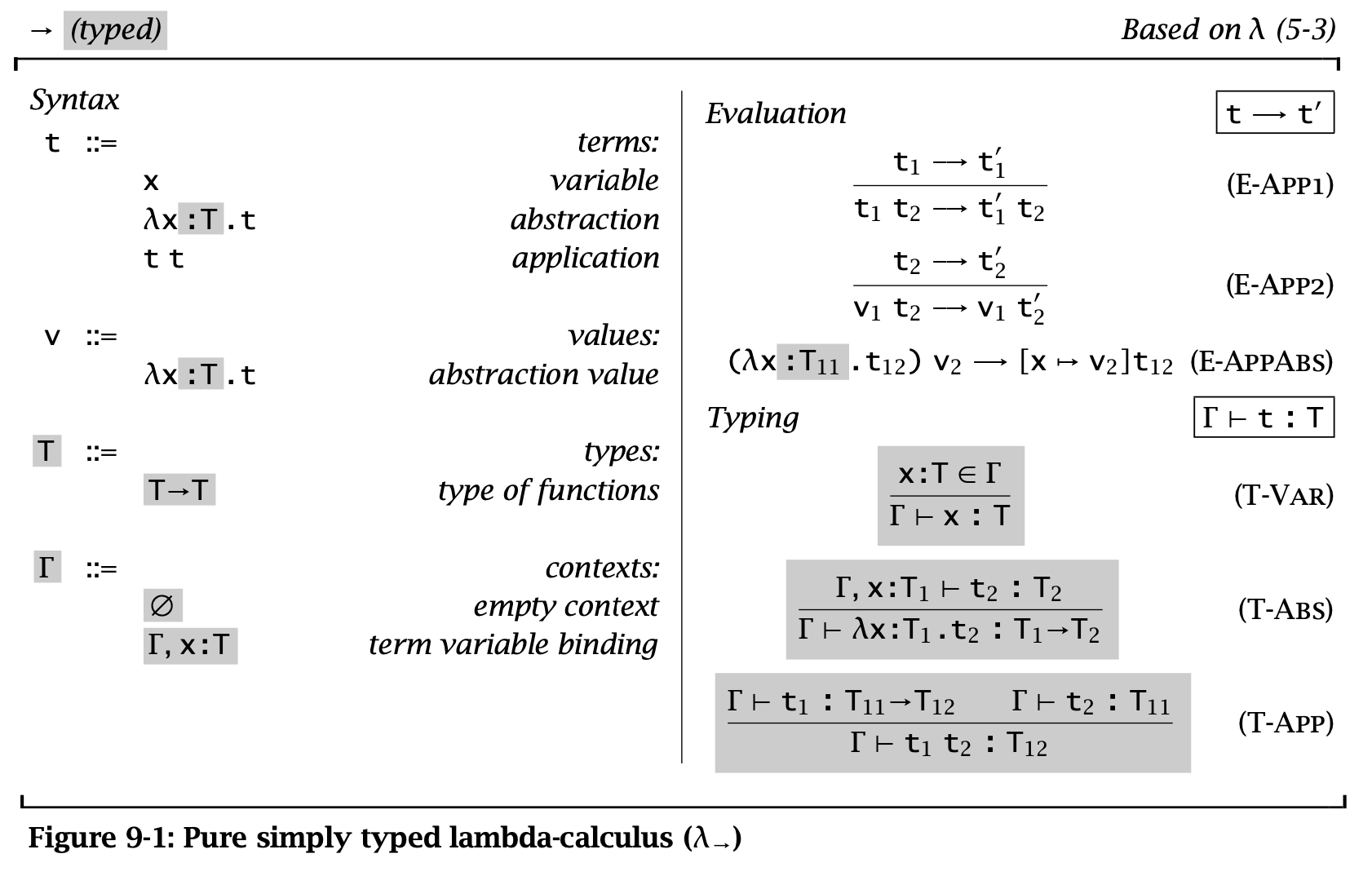
Figure 1: Pure Simply Typed λ Calculus
完整的 calculus 分成两部分,一部分是 pure STLC(图 9-1),另一部分则是 base type(图 8-1)。
通常用 \(\lambda_\rightarrow\) 来表示 STLC 和 STLC 加上 base type 的系统。
如果 STLC 中没有 base types(如 Bool),那么它是 degenerate,即其中没有 well-typed terms。因为没有 base types 那么就相当于归纳法中缺少了基础情况,不能构建其他类型。
Type Derivation Tree
\(\lambda_\rightarrow\) 的类型推导也能写成 derivation tree 的形式:
\[ \frac{ \frac{\frac{x : \operatorname{\mathtt{Bool}} \in x : \operatorname{\mathtt{Bool}}}{x : \operatorname{\mathtt{Bool}} \vdash \operatorname{\mathtt{Bool}}} \text{T-Var}}{\vdash \lambda x : \operatorname{\mathtt{Bool}} . x : \operatorname{\mathtt{Bool}} \rightarrow \operatorname{\mathtt{Bool}}} \text{T-Abs} \quad \frac{\qquad}{\vdash \operatorname{\mathtt{true}} : \operatorname{\mathtt{Bool}}} \text{T-True} } { \vdash (\lambda x : \operatorname{\mathtt{Bool}})\ \operatorname{\mathtt{true}} : \operatorname{\mathtt{Bool}} } \text{T-App} \]
Properties of Typing
Inversion
(Inversion of the typing relation)
- If \(\Gamma \vdash x : R\), then \(x : R \in \Gamma\)
- If \(\Gamma \vdash \lambda x : T . t_2 : R\), then \(R = T_1 \rightarrow R_2\) for some \(R_2\) with \(\Gamma, x : T_1 \vdash t_2 : R_2\)
- If \(\Gamma \vdash t_1\ t_2 : R\), then there is some type \(T_{11}\) such that \(\Gamma \vdash t_1 : T_{11} \rightarrow R\) and \(\Gamma \vdash t_2 : T_{11}\)
- If \(\Gamma \vdash \operatorname{\mathtt{true}} : R\), then \(R = \operatorname{\mathtt{Bool}}\).
- If \(\Gamma \vdash \operatorname{\mathtt{false}} : R\), then \(R = \operatorname{\mathtt{Bool}}\).
- If \(\Gamma \vdash \operatorname{\mathtt{if}} t_1 \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 : R\), then \(\Gamma \vdash t_1 : \operatorname{\mathtt{Bool}}, \Gamma \vdash t_2 : R, \Gamma \vdash t_3 : R\).
此处 typing rules 都是双射,易证。
是否存在 \(\Gamma \vdash x\ x : T\)?
不存在。假设存在,设 \(x : T_1 \rightarrow T_2\) 且 \(x : T_1\)。则 \(T_1 \rightarrow T_2 = T_1\),这样导致了无限长的类型,矛盾。但是如果允许无穷类型(recursive type),那么这个是可以成立的。
Uniqueness
前面在加类型的时候,只在 abstraction 的参数上加了,其他地方没有加。这是因为根据 Uniqueness of Types,类型和 term 是对应的。这表明类型可以从 term 中恢复(type reconstruction)。
(Uniqueness of Types)
In a given typing context \(\Gamma\), a term \(t\) (with free variables all in \(dom(\Gamma)\)) has at most one type. That is, if a term is typable, then its type is unique. Moreover, there is just one derivation of this typing built from the inference rules that generate the typing relation.
注解:这条性质对后面的类型系统不一定成立
Progress
(Canonical Forms)
- If \(v\) is a value of type \(\operatorname{\mathtt{Bool}}\), then \(v\) is either
trueorfalse. - If \(v\) is a value of type \(T_1 \rightarrow T_2\), then \(v = \lambda x : T_1. t_2\).
在 STLC 的 progress theorem 中,我们只关心 closed term,不考虑自由变量。(因为性质对 open terms 不成立)
(Progress)
Suppose \(t\) is a closed, well-typed term (\(\vdash t : T\)). Then either \(t\) is a value or else there is some \(t’\) with \(t \rightarrow t’\).
分情况讨论:
Boolean constants & if-conditions:上一章已经证明
Value/Abstraction:已经是 value
Application: \[ t = t_1\ t_2 \quad \text{where} \vdash t_1 : T_{11} \rightarrow T_{12}, \vdash t_2 : T_{11} \]
- 假设 \(t_1\) 能继续 evaluation,则可以用
E-App1 - 否则,假设 \(t_2\) 能继续 evaluation,则可以用
E-App2 - 否则,由 Canonical Forms Lemma 知 \(t_1 = \lambda x : T_{11}. t_{12}\),而可以用
E-AppAbs
- 假设 \(t_1\) 能继续 evaluation,则可以用
Preservation
下面有两个 lemmas 用来证明 STLC 的 preservation theorem,都可以通过对 typing derivations 进行 induction 证明。
(Permutation)
If \(\Gamma \vdash t : T\) and \(\Delta\) is a permutation of \(\Gamma\), then \(\Delta \vdash t : T\). Moreover, the latter derivation has the same depth as the former.
(Weakening)
If \(\Gamma \vdash t : T\) and \(x \notin dom(\Gamma)\), then \(Γ, x : S \vdash t : T\). Moreover, the latter derivation has the same depth as the former.
下面这个 lemma 证明了 well-typedness 在替换中可以被保持。
(The substitution lemma) (Preservation of types under substitution)
If \(\Gamma, x:S \vdash t:T\) and \(\Gamma \vdash s:S\), then \(\Gamma \vdash [x \mapsto s] t:T\).
(By induction on a derivation of the statement \(\Gamma, x : S \vdash t : T\))
T-Var即单变量的情况\[ t = z \quad \text{where}\ z : T \in (\Gamma, x : S) \]
- \(z = x\),而 \(t = z = x : S\),即 \(T = S\),则 \([x \mapsto s] t = [x \mapsto s] x = s : S\),成立
- \(z \neq x\),则 \([x \mapsto s]t = [x \mapsto s]z = z = t : T\),显然成立
T-Abs不妨设 \(x \neq y\) 且 \(y \notin FV(S)\)。
\begin{aligned} & t = \lambda y : T_2. t_1 \\ & T = T_2 \rightarrow T_1 \\ & \Gamma, x : S, y : T_2 \vdash t_1 : T_1 \end{aligned}
对 \(\Gamma, x : S, y : T_2 \vdash t_1 : T_1\) 用 permutation lemma 有 \(\Gamma, y : T_2, x : S \vdash t_1 : T_1\);
对 \(\Gamma \vdash s : S\) 用 weakening lemma 有 \(\Gamma, y : T_2 \vdash s : S\);
结合上面两条,以 \(\Gamma, y : T_2\) 为 context,由归纳假设知 \(\Gamma, y : T_2 \vdash [x \mapsto s] t_1 : T_1\);
再由
T-Abs有 \(\Gamma \vdash \lambda y : T_2. [x \mapsto s] t_1 : T_2 \rightarrow T_1\),即 \([x \mapsto s] t = \lambda y : T_1. [x \mapsto s] t_1 : T\)T-App\begin{aligned} & t = t_1\ t_2 : T \\ & \Gamma, x : S \vdash t_1 : T_2 \rightarrow T_1 \\ & \Gamma, x : S \vdash t_2 : T_2 \\ & T = T_1 \\ \end{aligned}
由归纳假设知
\begin{aligned} & \Gamma \vdash [x \mapsto s] t_1 : T_2 \rightarrow T_1 \\ & \Gamma \vdash [x \mapsto s] t_2 : T_2 \end{aligned}
由
T-App,成立T-True/T-False:Bool替换后值不变,类型不变T-If\begin{aligned} & t = \operatorname{\mathtt{if}} t_1 \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 \\ & \Gamma, x : S \vdash t_1 : \operatorname{\mathtt{Bool}} \\ & \Gamma, x : S \vdash t_2 : \operatorname{\mathtt{T}} \\ & \Gamma, x : S \vdash t_3 : \operatorname{\mathtt{T}} \\ \end{aligned}
由归纳假设可知
\begin{aligned} & \Gamma, x : S \vdash [x \mapsto s] t_1 : \operatorname{\mathtt{Bool}} \\ & \Gamma, x : S \vdash [x \mapsto s] t_2 : \operatorname{\mathtt{T}} \\ & \Gamma, x : S \vdash [x \mapsto s] t_3 : \operatorname{\mathtt{T}} \\ \end{aligned}
由
T-If,则 \([x \mapsto s] t : T\) 成立
Preservation
If \(\Gamma \vdash t:T\) and \(t \rightarrow t’\), then \(\Gamma \vdash t’:T\).
By induction on a derivation of the statement \(\Gamma, x : S \vdash t : T\)
T-True/T-False/T-Abs/T-Var:已经是 valueT-If:上一章已经证明T-App\[ t = t_1\ t_2 \quad \text{where}\ \Gamma \vdash t_1 : T_{11} \rightarrow T_{12}, \Gamma \vdash t_2 : T_{11}, T = T_{12} \]
如果能使用
E-App1,即 \(t_1 \rightarrow t_1’\),根据归纳假设,有 \(t_1’ : T_{11} \rightarrow T_{12}\),则 \(t_1’\ t_2 : T_{12} = T\)如果能使用
E-App2,同理否则需要
E-AppAbs,\(t_2 \rightarrow v_2 \text{ and } t_1\ t_2 = (\lambda x. t_{12})\ t_2 = [x \mapsto v_2] t_{12}\)由 inversion lemma 知 \(\Gamma, x : T_{11} \vdash t_1 : T\),又根据 substitution lemma,\([x \mapsto t_2] t_{12} : T\),即 \(t_1\ t_2 : T\)。
Subject expansion 对 STLC 的 functional part 成立吗(若 \(t\) 不包含条件表达式,\(t \rightarrow t’\) 且 \(\Gamma \vdash t’ : T\),则 \(t : T\))成立吗?
错误。
\((\lambda x : \operatorname{\mathtt{Bool}}. \lambda y : \operatorname{\mathtt{Bool}}. y)\ (\operatorname{\mathtt{true}}\ \operatorname{\mathtt{true}}) \rightarrow (\lambda y : \operatorname{\mathtt{Bool}}. y)\),而前者是 ill-typed。
The Curry-Howard Correspondence
Type constructor \(\rightarrow\) 有两个 typing rules:
- Introduction rule (T-Abs): how elements of the type can be created
- Elimination rule (T-App): how elements of the type can be used
当 introduction form(λ abstraction)是 elimination form(application)的 subterm 时,就构成了一个 redex,即可以进行计算(computation)。
Induction/Elimination 这两个词来自类型论和逻辑之间的联系,即 Curry-Howard Correspondence。其思想为:在构造主义逻辑中,命题 \(P\) 的证明由关于 \(P\) 的证据(evidence)组成,而证据有很强的计算属性。
| Logic | Programming Languages |
|---|---|
| propositions | types |
| proposition \(P \supset Q\) | type \(P \rightarrow Q\) |
| proposition \(P \wedge Q\) | type \(P \times Q\) |
| proof of proposition \(P\) | term \(t\) of type \(P\) |
| proposition \(P\) is provable | type \(P\) is inhabited (by some term) |
STLC 中的一个 term 是其类型对应的逻辑命题的一个证明。计算(computation)对应了逻辑运算中用来化简证明的 cut elimination。
由于 CH 同构的存在,逻辑和类型系统两个领域的进展往往可以相互转换。
如果在这个系统能再引入 fix,就会得到
\[\dfrac{\Gamma \vdash M : \tau \rightarrow \tau}{\Gamma \vdash \operatorname{\mathtt{fix}}\ : \tau}\]
也就是说不终止的证明可以证明任意命题成立,所以引入 fix 的系统是 inconsistent logic。
Erasure and Typability
很多编译器会在类型检查的阶段利用类型信息进行分析,但是在运行时会将类型信息抹掉,还原成无类型程序。这个过程可以用 erasure 函数完成。
(erasure)
The erasure of a simply typed term \( t \) is defined as follows:
\begin{aligned} & \operatorname{erase}(x) &&= x \\ & \operatorname{erase}(\lambda x : T_1 . t_2) &&= \lambda x. \operatorname{erase} (t_2) \\ & \operatorname{erase}(t_1\ t_2) &&= \operatorname{erase}(t_1)\ \operatorname{erase}(t_2) \\ \end{aligned}
下面证明直接对 typed term 进行求值和先抹掉类型信息再对 untyped term 进行求值,其结果不变。
Properties for erasure:
- If \(t \rightarrow t’\) under the typed evaluation relation, then \(\operatorname{erase}(t) \rightarrow \operatorname{erase}(t’)\).
- If \(\operatorname{erase}(t) \rightarrow m’\) under the untyped evaluation relation, then there is a simply typed term \(t’\) such that \(t \rightarrow t’\) and \(\operatorname{erase}(t’) = m’\).
(Straightforward induction on evaluation derivations)
下面这个性质和 type reconstruction 有关。
A term \(m\) in the untyped lambda-calculus is said to be typable in \(\lambda_\rightarrow\) if there are some simply typed term \(t\), type \(T\), and context \(\Gamma\) such that \(\operatorname{erase}(t) = m\) and \(\Gamma \vdash t : T\).
Curry-Style vs. Church-Style
目前有两种方式可以定义 STLC 的 semantics:
- 直接在 STLC 上定义的 evaluation relation
- 在 untyped λ calculus 上定义的 compilation 形式,再加上 untyped 的 evaluation rules
这两种形式共同点在于无论 term 是否 well-typed,都可以讨论其行为。
先定义 term,然后定义 semantics,再定义类型系统来去掉不合法的 term,这种方式称为 Curry Style。即 Semantics 优先于 Term。
另一种形式是定义了 term 后,先定义 well-typed terms,然后给出合法 term 的 semantics。这称为 Church Style。即 Term 优先于 Semantics。
在 Church style 中不会遇到 ill-typed term 的求值问题。实际上在 Church style 中,真正的求值过程发生在类型的推导上,而不是在 term 上。
在历史上,λ 演算的 implicitly typed presentation 通常用 Curry style,Church style 用于描述 explicitly typed systems。