Types
在 Chapter 3 中定义的 Untyped Arithmetic Expression 存在 stuck 的情况,例如 pred false。为了检查出这些错误,我们引入“类型”的概念。对于 Chapter 3 的表达式,需要用到 Nat 和 Bool 两种类型。
这里说 “term t has type T” 是不经过 evaluation 的情况下得到的信息。
例如 \(\operatorname{\mathtt{if}} \operatorname{\mathtt{true}} \operatorname{\mathtt{then}} \operatorname{\mathtt{false}} \operatorname{\mathtt{else}} \operatorname{\mathtt{true}}\) 的类型一定是 Bool,可以由规则推导得到;但是 \(\operatorname{\mathtt{if}} (\operatorname{\mathtt{iszero}} 0) \operatorname{\mathtt{then}} 0 \operatorname{\mathtt{else}} \operatorname{\mathtt{false}}\) 的具体类型则需要在 evaluation 后才能得到。
The Typing Relation
一个 typing relation \(t \in T\) 通常写作 \(t : T\),由一些从 type 到 term 的推导规则来指定。
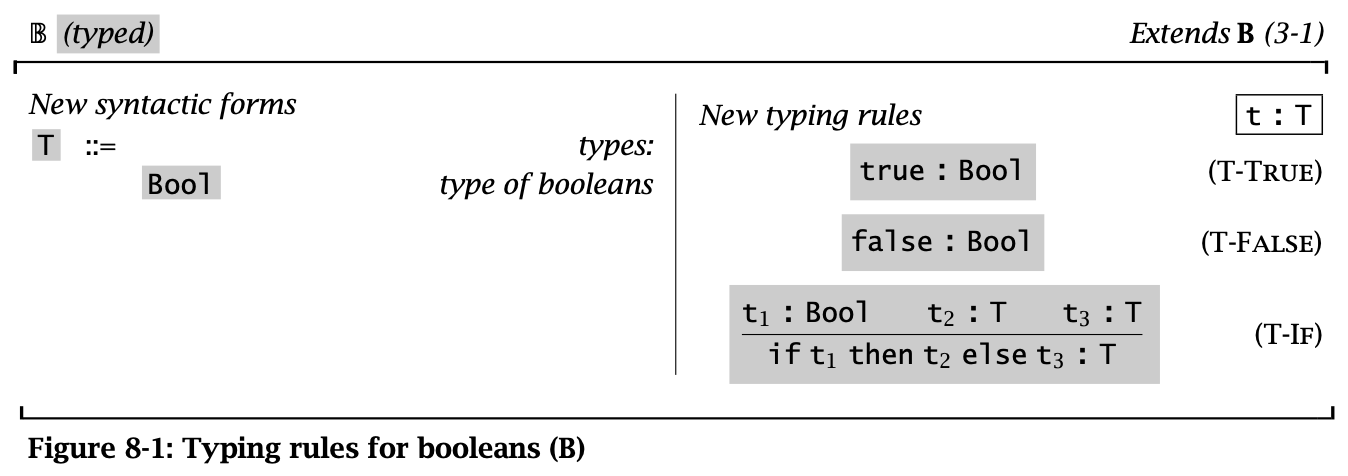
Figure 1: Typing rules for booleans
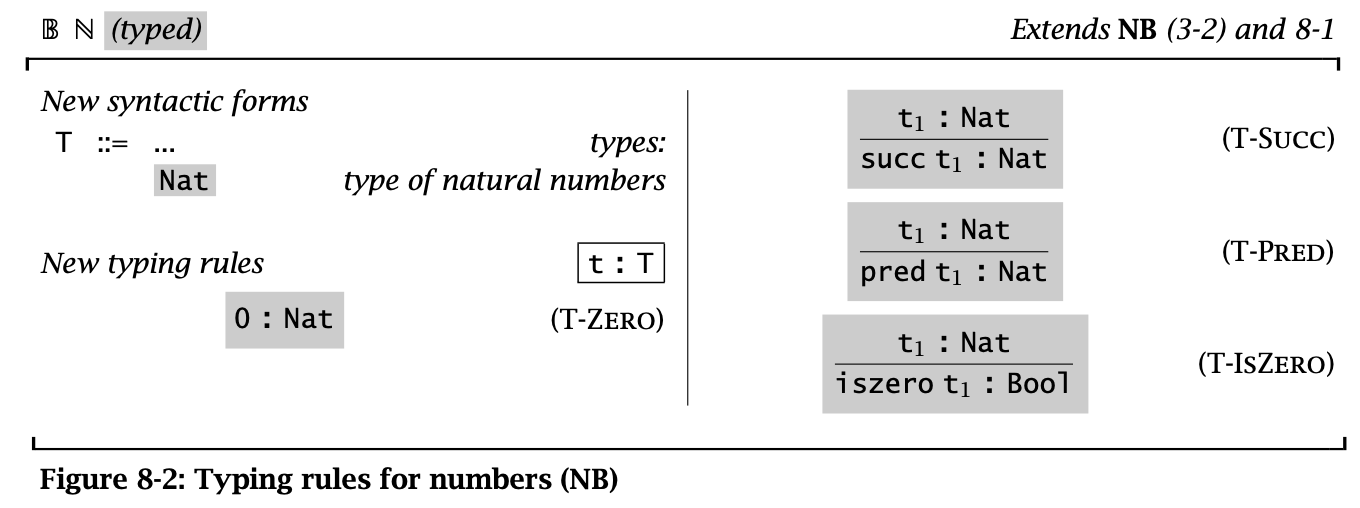
Figure 2: Typing rules for numbers
如图的 T-If 规则,要求 \(t_1 : \operatorname{\mathtt{Bool}}\),同时 \(t_2\) 和 \(t_3\) 为同一种类型 \(T\)。
(Well typed)
A term \(t\) is typable (or well typed) if there is some \(T\) such that \(t : T\).
Inversion
(Inversion of the typing relation) (Generation Lemma)
- If \(\operatorname{\mathtt{true}} : R\), then \(R = \operatorname{\mathtt{Bool}}\).
- If \(\operatorname{\mathtt{false}} : R\), then \(R = \operatorname{\mathtt{Bool}}\).
- If \(\operatorname{\mathtt{if}} t_1 \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 : R\), then \(t_1 : \operatorname{\mathtt{Bool}}, t_2 : R, t_3 : R\).
- If \(0 : R\), then \(R = Nat\).
- If \(\operatorname{\mathtt{succ}} t_1 : R\), then \(R = \operatorname{\mathtt{Nat}}\) and \(t_1 : \operatorname{\mathtt{Nat}}\).
- If \(\operatorname{\mathtt{pred}} t_1 : R\), then \(R = \operatorname{\mathtt{Nat}}\) and \(t_1 : \operatorname{\mathtt{Nat}}\).
- If \(\operatorname{\mathtt{iszero}} t_1 : R\), then \(R = \operatorname{\mathtt{Bool}}\) and \(t_1 : \operatorname{\mathtt{Nat}}\).
此处 typing rules 都是双射,易证。
通过 generation lemma,可以根据 term 的 syntactic form 来计算出其 type。类型的推导(typing derivation)可以也用一棵树来表示。
- Statements are formal assertions about the typing of programs.
- Typing rules are implications between statements
- Derivations are deductions based on typing rules.
Uniqueness
(Uniqueness of Types)
Each term \(t\) has at most one type. That is, if \(t\) is typable, then its type is unique. Moreover, there is just one derivation of this typing built from the inference rules.
注解 这条规则对于 subtyping 不适用
Safety = Progress + Preservation
类型系统最基本的特征在于 safety(soundness),即 well-typed 的 term 不会出错(陷入 stuck state)。这个性质包括两点:
- Progress: A well-typed term is not stuck
- either it is a value
- or it can take a step according to the evaluation rules
- Preservation: If a well-typed term takes a step of evaluation, then the resulting term is also well-typed.
- 而且大部分时候 evaluation 不会改变 type(但是 subtyping 中一个类型可能会变得 smaller)
Progress Theorem
(Canonical Forms)
- If \(v\) is a value of type
Bool, then \(v\) is eithertrueorfalse - If \(v\) is a value of type
Nat, then \(v\) is a numeric value.
Values 有四种可能:true、false、0、succ nv。根据 inversion lemma 4 和 5 可知后两种情况的类型是 Nat,排除。故命题 1 成立。
同理可证明命题 2。
(Progress)
Suppose \(t\) is a well-typed term (\(t : T\)). Then either \(t\) is a value or else there is some \(t’\) with \(t \rightarrow t’\).
By induction on a derivation of \(t : T\)
对于 T-True、T-False、T-Zero 显然成立,因为此时已经是 value。
T-If\[ \operatorname{\mathtt{if}} t_1 \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 \quad (t_1 : \operatorname{\mathtt{Bool}}) \]
- 如果 \(t_1\) 是 value,则根据 canonical forms lemma,它一定是
true或者false,则可以应用E-IfTrue或者E-IfFalse - 否则可以对 \(t_1\) 使用
E-If
- 如果 \(t_1\) 是 value,则根据 canonical forms lemma,它一定是
T-Pred\[ t = \operatorname{\mathtt{pred}} t_1 \quad (t_1 : \operatorname{\mathtt{Nat}}) \]
- 如果 \(t_1\) 是 value,则根据 canonical forms lemma,它一定是
0或者succ nv,则可以应用E-PredZero或者E-PredSucc - 否则可以使用
E-Pred
- 如果 \(t_1\) 是 value,则根据 canonical forms lemma,它一定是
T-Succ/T-IsZero同上
Preservation Theorem
(Preservation)
If \(t : T\) and \(t \rightarrow t’\), then \(t’ : T\).
By induction on a derivation of \(t : T\)
T-True/T-False/T-Zero排除,此时无法进行 evaluationT-If\[ \operatorname{\mathtt{if}} t_1 \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 \quad (t_1 : \operatorname{\mathtt{Bool}}; t_2, t_3 : T) \]
E-True/E-False\(t_1\) 为
true/false,结果为 \(t_2\) / \(t_3\)。此时表达式的类型均为TE-If\(t_1 \rightarrow t_1’\),由归纳假设知 \(t_1’ : \operatorname{\mathtt{Bool}}\),再由 canonical forms lemma 和
T-If知 \(\operatorname{\mathtt{if}} t_1’ \operatorname{\mathtt{then}} t_2 \operatorname{\mathtt{else}} t_3 : T\),则命题成立
T-Succ\[ t = \operatorname{\mathtt{succ}} t_1 \]
此时只能用
E-Succ这条规则使得 \(t \rightarrow t’\),即只要证明succ t' : Nat。由归纳假设知t' : Nat,则成立。
Preservation theorem 也被称为 subject reduction / subject evaluation。这个名称来自于 \(t : T\) 表示 “\(t\) has type \(T\)",其中 \(t\) 是句子的 subject。
Type Safe
在所有的类型系统(包括 subtyping)中,这两个定理都成立,否则就不是 type-safe 的。
但是存在一些特殊情况。例如使用 small-step 形式化 Java 的 operational semantics 时,preservation 就不再成立了。但是使用 big-step 就不会有这个问题,所以还是认为它是 type-safe 的。
几个有趣的问题:
E-PredZero 这条规则看起来比较违反直觉,能不能直接去掉?
不能,因为这样会破坏 progress property。要去掉的话需要使用 exception。或者使用 intersection type/dependent type 定义严格的“正数”。
Subject reduction 的逆操作 subject expansion(若 \(t \rightarrow t’\) 且 \(t’ : T\),则 \(t : T\))成立吗?
错误,\(\operatorname{\mathtt{if}} \operatorname{\mathtt{false}} \operatorname{\mathtt{then}} \operatorname{\mathtt{true}} \operatorname{\mathtt{else}} 0 \rightarrow 0\),而前者是 ill-typed。
对于 big-step 语义如何保证类型安全?
- Preservation (similar) If a well-typed term evaluates to some final value, then this value has the same type as the original term.
- Progress (stronger) Every well-typed term can be evaluated to some final value. (Evaluation always terminates on well-typed terms.)
注解 在 big-step 中 Progress property 并不总是成立的(例如在支持 general recursion 的语言中),因为没有办法区分 error state 和 termination。一个解决方案是为此提供一个前面提到过的 explicit wrong translation。