Introduction
用类似于 BNF 的 grammar 定义一个简单的语言:
[Terms, Grammarly]
\begin{aligned} t \Coloneqq & & (\text{terms}) \\ & \mathtt{true} & (\text{constant}\ \mathtt{true}) \\ & \mathtt{false} & (\text{constant}\ \mathtt{false}) \\ & \mathtt{if}\ t\ \mathtt{then}\ t\ \mathtt{else}\ t & (\text{conditions}) \\ & \mathtt{0} & (\text{constant}\ 0) \\ & \mathtt{succ}\ t & (\text{successor}) \\ & \mathtt{pred}\ t & (\text{predecessor}) \\ & \mathtt{iszero}\ t & (\text{zero}\ test) \end{aligned}
\(t\) 是一个 meta-variable(相当于一个 placeholder)。
这里定义的语法可能会生成一些 nonsensical 的程序,例如:succ 0,后面需要通过类型系统排除。
这里没有提到括号的用法,但是为了看起来清楚一点,写的时候会加上括号,如 iszero (pred (succ 0)) → true。
Syntax
[Terms, Inductively]
The set of terms is the smallest set \(\mathcal{T}\)
- \(\{ \mathtt{true}, \mathtt{false}, \mathtt{0} \} \subseteq \mathcal{T}\);
- if \(t_1 \in \mathcal{T}\), then \(\{\mathtt{succ}\ t_1, \mathtt{pred}\ t_1, \mathtt{iszero}\ t_1\} \subseteq \mathcal{T}\);
- if \(t_1 \in \mathcal{T}, t_2 \in \mathcal{T}, t_3 \in \mathcal{T}\), then \(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3 \in \mathcal{T}\).
[Terms, by Inference Rules]
The set of terms is defined by the following rules:
\[\mathtt{true} \in \mathcal{T}\]
\[\mathtt{false} \in \mathcal{T}\]
\[\mathtt{0} \in \mathcal{T}\]
\[\frac{t_1 \in \mathcal{T}}{\mathtt{succ}\ t_1 \in \mathcal{T}}\]
\[\frac{t_1 \in \mathcal{T}}{\mathtt{pred}\ t_1 \in \mathcal{T}}\]
\[\frac{t_1 \in \mathcal{T}}{\mathtt{iszero}\ t_1 \in \mathcal{T}}\]
\[\frac{t_1 \in \mathcal{T}, t_2 \in \mathcal{T}, t_3 \in \mathcal{T}}{\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3 \in \mathcal{T}}\]
关于 influence rules,需要注意的是
- 如果一个 rule 没有 premises,那么被称为 axioms
- 由于这里的 premises 和 conclusion 里面有 metavariables,所以严谨地说它们是 rule schemas
[Terms, Concretely] For each natural number \(i\), define a set \(S_i\) as follows:
\begin{alignat*}{2} S_0 = {}& \emptyset \\ S_{i+1} = {}&&& \{\mathtt{true}, \mathtt{false}, \mathtt{0}\} \\ & \cup {}&& \{\mathtt{succ}\ t_1, \mathtt{pred}\ t_1, \mathtt{iszero}\ t_1 \mid t_1 \in S_i\} \\ & \cup {}&& \{\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3 \mid t_1, t_2, t_3 \in S_i\} \end{alignat*}
Finally, let
\[S = \bigcup_i S_i\]
注:可以证明 \(S_i \subseteq S_{i+1}\)。
\(\mathcal{T} = S\)
由于 \(\mathcal{T}\) 是满足 inductively 定义条件的最小集合,所以只要证明 \(S\) 也是满足 inductively 定义的最小集合即可。即证明:
- \(S\) 满足 inductively 定义的条件
- 对于 \(\{\mathtt{true}, \mathtt{false}, 0\}\) 显然成立
- 对于 \(\mathtt{f}\ t\),有 \(t \in S \Rightarrow \exist i,t \in S_i \Rightarrow \mathtt{f}\ t \in S_{i+1} \subseteq S\)
- 任何满足 inductively 定义的集合 \(S’\) 都包含 \(S\) (即 \(S\) 是满足条件的最小集合)
- 考虑证明 \(\forall i, S_i \subseteq S’\)
- 归纳证明 \(\forall j < i, S_j \subseteq S’ \Rightarrow S_i \subseteq S’ \Rightarrow S = \bigcup_i S_i \subseteq S’\)
- 考虑证明 \(\forall i, S_i \subseteq S’\)
Induction on terms
根据 \(\mathcal{T} = S\),可以递归定义出一些关于集合 \(S\) 的函数,也可以对于 terms 的命题进行递归证明。
(Consts(t)):\(\mathtt{t}\) 中出现的常量的集合。
\begin{aligned} & \operatorname{Consts}(\mathtt{true}) &&= \{\mathtt{true}\} \\ & \operatorname{Consts}(\mathtt{false}) &&= \{\mathtt{false}\} \\ & \operatorname{Consts}(\mathtt{0}) &&= \{\mathtt{0}\} \\ & \operatorname{Consts}(\mathtt{succ}\ t_1) &&= \operatorname{Consts}(t_1) \\ & \operatorname{Consts}(\mathtt{pred}\ t_1) &&= \operatorname{Consts}(t_1) \\ & \operatorname{Consts}(\mathtt{iszero}\ t_1) &&= \operatorname{Consts}(t_1) \\ & \operatorname{Consts}(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3) &&= \operatorname{Consts}(t_1) \cup \operatorname{Consts}(t_2) \cup \operatorname{Consts}(t_3) \end{aligned}
Size(t):\(\mathtt{t}\) 的大小, 可以看作是语法树中的节点个数
\begin{aligned} & \operatorname{Size}(\mathtt{true}) &&= 1 \\ & \operatorname{Size}(\mathtt{false}) &&= 1 \\ & \operatorname{Size}(\mathtt{0}) &&= 1 \\ & \operatorname{Size}(\mathtt{succ}\ t_1) &&= \operatorname{Size}(\mathtt{true}) + 1 \\ & \operatorname{Size}(\mathtt{pred}\ t_1) &&= \operatorname{Size}(\mathtt{true}) + 1 \\ & \operatorname{Size}(\mathtt{iszero}\ t_1) &&= \operatorname{Size}(\mathtt{true}) + 1 \\ & \operatorname{Size}(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3) &&= \operatorname{Size}(t_1) + \operatorname{Size}(t_2) + \operatorname{Size}(t_3) + 1 \\ \end{aligned}
depth(t):语法树的深度
\begin{aligned} & \operatorname{depth}(\mathtt{true}) &&= 1 \\ & \operatorname{depth}(\mathtt{false}) &&= 1 \\ & \operatorname{depth}(\mathtt{0}) &&= 1 \\ & \operatorname{depth}(\mathtt{succ}\ t_1) &&= \operatorname{depth}(\mathtt{true}) + 1 \\ & \operatorname{depth}(\mathtt{pred}\ t_1) &&= \operatorname{depth}(\mathtt{true}) + 1 \\ & \operatorname{depth}(\mathtt{iszero}\ t_1) &&= \operatorname{depth}(\mathtt{true}) + 1 \\ & \operatorname{depth}(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3) &&= \max \left( \operatorname{depth}(t_1) + \operatorname{depth}(t_2) + \operatorname{depth}(t_3) \right) + 1 \\ \end{aligned}
\(\mid \operatorname{Consts}(t) \mid \leq \operatorname{size}(t)\)
分为 3 个 cases
\(t\) 是 constants:
\[ \mid \operatorname{Consts}(t) \mid = \mid \{ t \} \mid = 1 = \operatorname{size}(t) \]
\(t\) 是 \(\mathtt{succ}\ t_1\) 或 \(\mathtt{pred}\ t_1\) 或 \(\mathtt{iszero}\ t_1\)
\[ \mid \operatorname{Consts}(t) \mid = \mid \operatorname{Consts}(t_1) \mid \le \operatorname{size}(t_1) < \operatorname{size}(t) \]
\(t\) 是 \(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3\):
\begin{aligned} \mid \operatorname{Consts}(t) \mid = &\ \mid \operatorname{Consts}(t_1) \cup \operatorname{Consts}(t_2) \cup \operatorname{Consts}(t_3) \mid \\ \leq &\ \mid \operatorname{Consts}(t_1) \mid + \mid \operatorname{Consts}(t_2) \mid + \mid \operatorname{Consts}(t_3) \mid \\ \leq &\ \operatorname{size}(t_1) + \operatorname{size}(t_2) + \operatorname{size}(t_3) \\ < &\ \operatorname{size}(t) \end{aligned}
Theorem: Principles of induction on terms
(Principles of induction on terms)
Suppose \(P\) is a predicate on terms. Structural induction:
- If, for each term s,
- given \(P( r)\) for all immediate subterms \(r\) of \(s\)
- we can show \(P(s)\)
- then \(P(s)\) holds for all \(s\)
Semantic Styles
- Syntax(语法):程序的结构
- Semantic(语义):程序的值
Operational semantics
Operational semantics 分为 small-step 和 big-step。
Operational Semantics 用一个 abstract machine 来定义程序的语义,machine 的每一个状态都是一个 term,状态之间用 transition function(对 \(t\) 进行 simplification,或者终止程序)进行转移。machine 一开始的状态是 \(t\),终止状态为 \(t\) 的值。
通常一种语言会有多种 operational semantics,一种是贴近人的,另一种是贴近解释器或编译器的。证明这两种语义相同相当于证明语言实现的正确性。
Denotational semantics
Denotational semantics 将 term 看作是数学上的实体(通常是函数)。
Denotational Semantics 首先确定了一个 semantics domains,然后定义一个 interpretation function 将 term 映射到 semantics domains(domain theory)。
Denotational Semantics 好处在于可以突出语言的核心概念,并且 semantics domain 可以导出许多 laws,比如用来确定两个程序是否相同。
Axiomatic semantics
以上两种 semantics 都是先定义语言的行为,然后导出一些 laws。而 Axiomatic Semantics 将 laws 本身作为程序的定义(Hoare Logic)。
Evaluation
Booleans
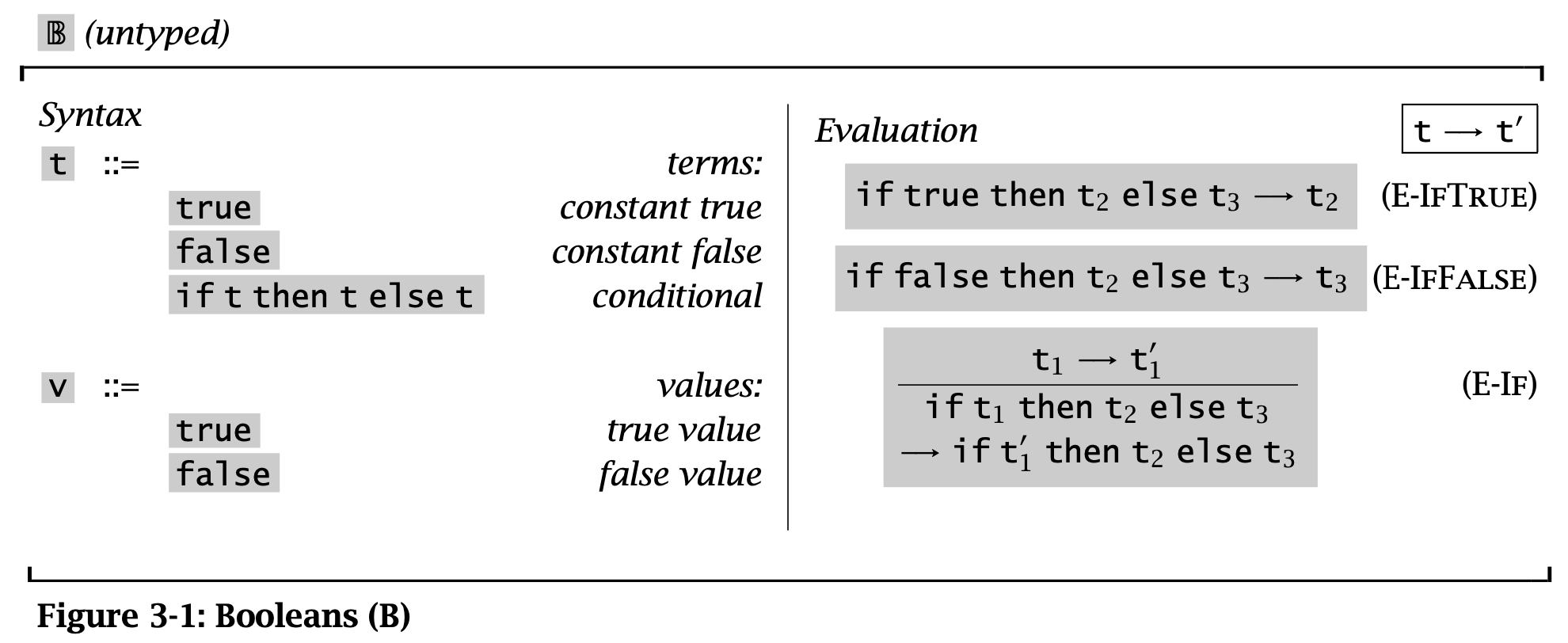
Figure 1: 3-1 Booleans
如图定义了 Booleans 的 syntax 和 semantics(即右边定义的 evaluation reduction,在 big-step 中称为 evaluation relation)。
前两条规则比较简单,重要的是第三条规则 E-If,它表明 if 语句的 guard t_1 可以被化简。而对于 then 分支和 else 分支不存在类似的规则,即必须从外到内化简。例如,不允许:
\[ \dfrac { \mathtt{if}\ \operatorname{\mathtt{true}}\ \mathtt{then}\ (\mathtt{if}\ \operatorname{\mathtt{false}}\ \mathtt{then}\ \operatorname{\mathtt{false}}\ \mathtt{else}\ \operatorname{\mathtt{false}} ) \mathtt{else}\ \operatorname{\mathtt{true}} } { \mathtt{if}\ \operatorname{\mathtt{true}}\ \mathtt{then}\ \operatorname{\mathtt{false}}\ \mathtt{else}\ \operatorname{\mathtt{true}} } \]
E-If 的作用是决定哪里需要化简,而 E-IfThen 和 E-IfElse 真正进行了化简工作,所以前者称为 congruence rule,后者称为 computation rules。
(Rules)
- An instance of an inference rule is obtained by consistently replacing each metavariable by the same term in the rule’s conclusion and all its premises (if any).
- A rule is satisfied by a relation if, for each instance of the rule, either the conclusion is in the relation or one of the premises is not.
One-step evaluation relation
(One-step evaluation relation \(\rightarrow\))
- The one-step evaluation relation \(\rightarrow\) is the smallest binary relation on terms.
- When the pair \((t,t’)\) is in the evaluation relation, we say that “the evaluation statement (or judgment) \(t \rightarrow t’\) is derivable.”
(Derivability)
An evaluation statement \(t \rightarrow t’\) is derivable iff. there is a derivation tree with \(t \rightarrow t’\) as the label at its root.
在一颗 derivation tree 上,E-If 是 internal nodes,E-True 和 E-False 是 leaf nodes。
(Determinacy of one-step evaluation)
If \(t \rightarrow t’\) and \(t \rightarrow t’’\), then \(t’ = t’’\).
Induction on evaluation derivations.
- 假设最后一条规则是
E-IfTrue,则 \(t\) 为 \(\mathtt{if}\ \mathtt{true}\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3\),此时显然不能用E-IfFalse或E-If(因为 guard 不能化简了),则 \(t’’ = t_2 = t’\)。(E-IfFalse同理) - 假设最后一条规则是
E-If,则 \(t\) 为 \(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3\),且 \(t_1 \rightarrow t_1’\)。由于 \(t_1\) 可以被化简,非 \(\mathtt{true} \mid \mathtt{false}\),此时只能用E-If:\(t_1 \rightarrow t_1’’\)。由归纳假设知 \(t_1’ = t_1’’\),则 \(t’ = t’’\)
Normal Forms
(Normal Form)
A term \(t\) is in normal form if no evaluation rule applies to it.
显然,true 和 false 是 normal forms,因为没有针对它们的求解规则。
Every value is in normal form.
If \(t\) is in normal form, then \(t\) is a value.
考虑证明逆否命题:不是 value 的都不是 normal forms。
由规则知,如果 \(t\) 不是 value,那么它一定是 \(\mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3\) 的形式。
- 当 \(t_1 = \mathtt{true} \mid \mathtt{false}\),可以应用
E-IfTrue/E-IfFalse,所以不是 normal form - 否则可以用
E-If
注解:只对当前的系统成立,对于后面的系统不一定成立
所有的 values 都是 normal form,但是 normal form 不一定都是 values。
Multi-step evaluation relation
(Multi-step evaluation relation \(\rightarrow^\star\))
The multi-step evaluation relation \(\rightarrow^∗\) is the reflexive, transitive closure of one-step evaluation. That is, it is the smallest relation such that - if \(t \rightarrow t’\) then \(t \rightarrow^* t’\) - \(t \rightarrow^* t\) for all \(t\) (reflexivity) - if \(t \rightarrow^* t’\), \(t’ \rightarrow^* t’’\), then \(t \rightarrow t’’\) (transitivity)
注解:是 \(\rightarrow^\ast\),而不是 \(^\ast t\)
Confluence
(Uniqueness of normal forms)
If \(t \rightarrow^* u\) and \(t \rightarrow^* u’\), where \(u\) and \(u’\) are both normal forms, then \(u = u’\).
由 Determinacy of one-step evaluation 显然。
(Diamond Property)
If \(r \rightarrow s\) and \(r \rightarrow t\), with \(s \neq t\), then there is some term \(u\) such that \(s \rightarrow u\) and \(t \rightarrow u\).
添加一条规则:
\[ \dfrac{ t_2 \rightarrow t_2' } { \mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3 \rightarrow \mathtt{if}\ t_1\ \mathtt{then}\ t_2’\ \mathtt{else}\ t_3 } \text{[E-Funny2]} \]
这条规则满足 Diamond Property.
Induction on the pair of derivations.
显然这种情况只有可能在 \(r:\mathtt{if}\ r_1\ \mathtt{then}\ r_2\ \mathtt{else}\ r_3\) 时发生:
- \(r \rightarrow s\) by
E-IfTrue, \(r \rightarrow t\) byE-Funny2- \(s: r_2\),即 \(r_1 = \mathtt{true}\)
- \(t: \mathtt{if}\ \mathtt{true}\ \mathtt{then}\ r_2’\ \mathtt{else}\ r_3\),即 \(r_2 \rightarrow r_2’\)
- 令 \(u = r_2’\)。对 \(s\) 用 \(r_2 \rightarrow r_2’\),对 \(t\) 使用
E-IfTrue - 则 \(s \rightarrow u\), \(t \rightarrow u\)
- 其他使用规则不同的情况类似
- \(r \rightarrow s\) by
E-If, \(r \rightarrow t\) byE-If- \(s: \mathtt{if}\ r_1’\ \mathtt{then}\ r_2\ \mathtt{else}\ r_3\)
- \(t: \mathtt{if}\ r_1’’\ \mathtt{then}\ r_2\ \mathtt{else}\ r_3\)
- 根据归纳假设,\(r_1 \rightarrow r_1’ \rightarrow r_1’’’\), \(r_1 \rightarrow r_1’’ \rightarrow r_1’’’\)
- 令 \(u = \mathtt{if}\ r_1’’’\ \mathtt{then}\ r_2\ \mathtt{else}\ r_3\),则 \(s \rightarrow u\), \(t \rightarrow u\) by
E-If - 其他使用规则相同的情况类似
通过 Diamond Property 可以直接推出 Uniqueness。
Termination
Termination proofs 的证明形式:
- 首先找到一个良基集(well-founded set,满足良序关系的集合)\(S\) ,以及一个将 machine state 映射到 \(S\) 的函数 \(f\)(称为 termination measure)
- 证明对于 \(t \rightarrow t’\),\(f(t’) < f(t)\)
- 由良基集的定义知:求解会终止
(Termination of Evaluation)
For every term \(t\) there is some normal form \(t’\) such that \(t \rightarrow t’\)
可以发现每一步求解都会使得 \(\operatorname{size}\) 减小,所以令 \(f = \operatorname{size}\) 为 termination measure,以 \(S = \mathbb{N}\) 为良基集
注解:这条规则也并非恒成立,后面会用类型系统对一些语言进行 termination proof
Arithmetic expressions
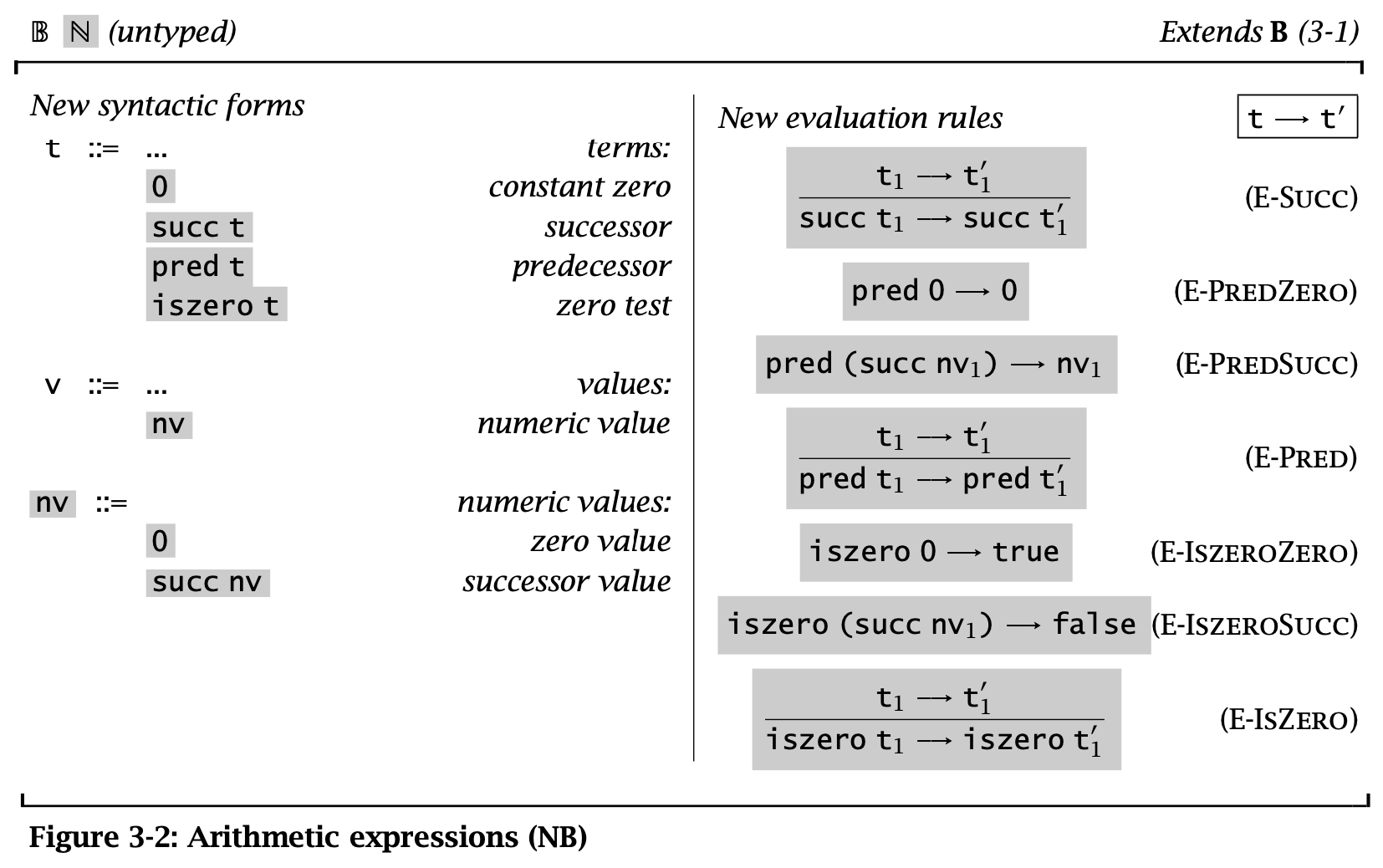
Figure 2: 3-2 Arithmetic Expressions
succ(true) 是非法的。
在计算 pred (succ (pred 0)) 时,不能直接应用 E-PredSucc,因为其参数为 nv,而 pred 0 并非 nv。所以必须用 derivation tree。
\[ \frac{ \frac{ \frac{\quad}{\mathtt{pred} 0 \rightarrow 0} \text { E-PredSucc } } { \mathtt{succ} (\mathtt{pred} 0) \rightarrow \mathtt{succ} 0}{\text { E-Succ } } }{ \mathtt{pred}(\mathtt {succ}(\mathtt { pred } 0)) \rightarrow \mathtt { pred }(\mathtt{succ} 0)} \text { E-Pred } \]
显然,One-step evaluation relation 对于 Arithmetic Expressions 也成立。
Stuckness
(Stuckness)
A closed term is stuck if it is in normal form but not a value.
注解:Stuckness 意味着 operational semantics 遇到了 runtime errors。在这里表现为化简不下去。例如 succ true
wrong
处理 stuckness 的一种方法:增加一种新的 term wrong。下面是一个例子:
\begin{aligned} \mathtt{badnat} \Coloneqq & & (\text{non-numeric normal forms}) \\ & \mathtt{wrong} & (\text{run-time error}) \\ & \mathtt{true} & (\text{constant}\ \mathtt{true}) \\ & \mathtt{false} & (\text{constant}\ \mathtt{false}) \\ \end{aligned}
\begin{aligned} \mathtt{badbool} \Coloneqq & & (\text{non-boolean normal forms}) \\ & \mathtt{wrong} & (\text{run-time error}) \\ & \mathtt{nv} & (\text{numeric}) \\ \end{aligned}
\[ \mathtt{if}\ \mathtt{badbool}\ \mathtt{then}\ t_1\ \mathtt{else}\ t_2 \rightarrow \mathtt{wrong} \tag{E-If-Wrong} \]
\[ \mathtt{succ}\ \mathtt{badbool} \rightarrow \mathtt{wrong} \tag{E-Succ-Wrong} \]
\[ \mathtt{pred}\ \mathtt{badbool} \rightarrow \mathtt{wrong} \tag{E-Pred-Wrong} \]
\[ \mathtt{iszero}\ \mathtt{badbool} \rightarrow \mathtt{wrong} \tag{E-IsZero-Wrong} \]
Big-step Evaluation
前面用的都是 Small-step Evaluation,另外一种是 Big-step Evaluation(也叫 natural evaluation):
- 证明起来更简单
- 不能描述无法求值的过程(会 stuck)
二者的区别在于:
- Small-step Evaluation:如何一步步对程序进行规约
- 设表达式是 \(E\),则规约规则 \(\rightarrow: E \times E\)
- 在实现上 small-step 会不断对整个表达式应用 rules
- Big-step Evaluation:定义如何从一个表达式或者语句直接得到它的结果(假设各部分都已经规约完毕了)
- 设表达式是 \(E\),value 是 \(V\),则规约规则 \(\Downarrow: E \times V\)
- 在实现上,big-step 着重于寻找表达式的 value,会直接对每个部分进行递归求值
\[ v \Downarrow v \qquad \tag{B-Value} \]
\[ \dfrac { t_1 \Downarrow \mathtt{true} \qquad t_2 \Downarrow v_2 } { \mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3 \Downarrow v_2 } \tag{B-IfTrue} \]
\[ \dfrac { t_1 \Downarrow \mathtt{false} \qquad t_3 \Downarrow v_3 } { \mathtt{if}\ t_1\ \mathtt{then}\ t_2\ \mathtt{else}\ t_3 \Downarrow v_3 } \tag{B-IfFalse} \]
\[ \dfrac{t_1 \Downarrow \mathtt{nv}_1}{\mathtt{succ}\ t_1 \Downarrow \mathtt{succ}\ \mathtt{nv}_1} \tag{B-Succ} \]
\[ \dfrac{t_1 \Downarrow 0}{\mathtt{pred\ t_1 \Downarrow 0}} \tag{E-PredZero} \]
\[ \dfrac{t_1 \Downarrow \mathtt{succ}\ \mathtt{nv}_1}{\mathtt{pred}\ t_1 \Downarrow \mathtt{nv}_1} \tag{E-PredSucc} \]
\[ \dfrac{t_1 \Downarrow 0}{\mathtt{iszero}\ t_1 \Downarrow 0} \tag{B-IszeroZero} \]
\[ \dfrac{t_1 \Downarrow \mathtt{succ}\ \mathtt{nv}_1}{\mathtt{iszero}\ t_1 \Downarrow \mathtt{false}} \tag{B-IszeroSucc} \]