泵引理
(Pumping Lemma for CFL)
对于任何 CFL \(L\),存在仅依赖 \(L\) 的正整数 \(N\),使得对于任意 \(z \in L\),当 \(|z| \ge N\) 时,存在 \(u, v, w, x, y\),满足 \(z = u v w x y\) 且:
- \(|v w x| \le N\)
- \(|vx| \ge 1\)
- \(u v^i w x^i y \in L\ (i = 0, 1, \dots)\)(或者等价表述为 \(\exists A \in V. S \xRightarrow{*} uAy; A \xRightarrow{*} vAx | w\))
假设 CFL \(L\),不妨先假设 \( \varepsilon \notin L \),那么存在 CNF \( G = (V, T, P, S) \) 使得 \( L = L(G) \)。此时 \( G \) 所产生的派生树一定是一颗二叉树。对于任意 \( z \in L \),设 \( k \) 是树上最长路径,则有 \( |z| \le 2^{k-1} \),且仅当语法树是满二叉树时等号成立。
取 \( N = 2^{|V|} = 2^{|V| + 1 - 1} \),并取 \(z \in L\ (|z| \ge N)\),则此时 \( z \) 的语法树中至少有一条长度大于等于 \( |V| + 1 \) 的路径 \( p \),路径上的非叶节点(语法变量)数量大于等于 \( |V| + 1 \)。根据鸽巢原理,路径上必定有两个相同的语法变量。
取路径上的两个最接近叶子且表示同一语法变量的结点 \(v_1, v_2\)(不妨设 \(v_1\) 是 \(v_2\) 的祖先,且它们都表示 \(A\))。根据抽屉原理,\(v_1\) 到叶节点的路径小于等于 \(|V| + 1\)(否则就不是“最接近叶子”的)。设(如下图):
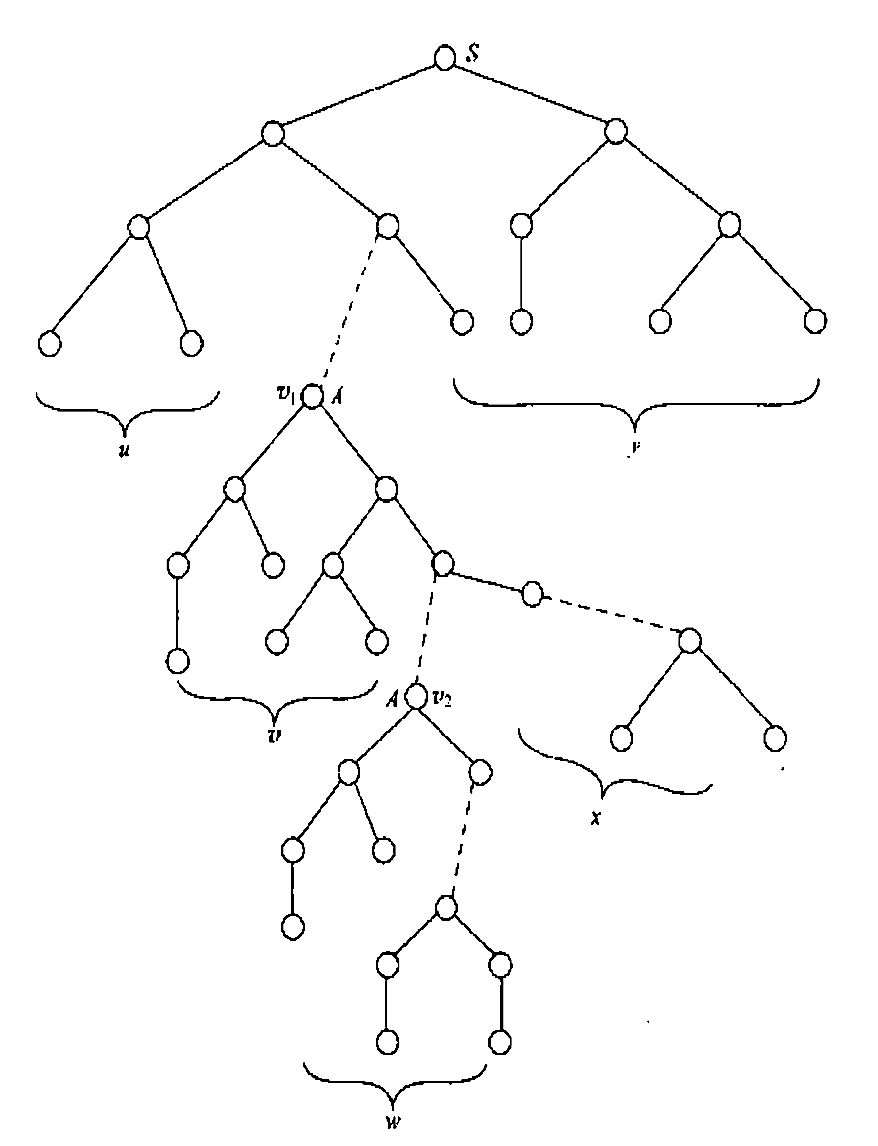
Figure 1: derivation tree for z
- 结点 \(v_1\) 左侧的所有叶结点构成的字符串为 \(u\)
- 结点 \(v_1\) 为根的子树中,\(v_2\) 左侧的叶节点构成 \(v\)
- 结点 \(v_2\) 为根的子树构成 \(w\)
- 结点 \(v_1\) 为根的子树中,\(v_2\) 右侧的叶节点构成 \(x\)
- 结点 \(v_1\) 右侧的所有叶节点构成 \(y\)
此时有 \(z = uvwxy\)。
由于以 \(v_1\) 为根的 \(A\) 子树的最长路长小于等于 \(|V| + 1\),因此有
\[|vwx| \le 2^{(|V| + 1) - 1} = 2^{|V|} = N\]
由于 \(G\) 是 CNF,因此不存在 \(v_1 \rightarrow v_2\),即
\[|vx| \ge 1\]
此时有
\[S \xRightarrow{*} uAy \xRightarrow{+} uvAxy \xRightarrow{+} uvwxy\]
显然,此处有 \(A \xRightarrow{*} v^iAx^i \xRightarrow{+} v^i w x^i\),因此有
\[S \xRightarrow{*} uAy \xRightarrow{+} uv^iAx^iy \xRightarrow{+} uv^iwx^iy\]
即 \(\forall i = 0, 1, \dots. uv^iwx^iy \in L\),成立。
CFL 上的泵引理的用法与 RL 的泵引理一致,通常使用反证法来证明一个语言不是 CFL。
Ogden 引理
Ogden 定理的证明
(Ogden Lemma)
对于任意 CFL \(L\),存在仅依赖于 \(L\) 的一个正整数 \(N\),使得对于任意 \(z \in L\),如果在 \(z\) 中标记至少 \(N\) 个特异点(distinguished positions),则存在 \(u, v, w, x, y\) 使得 \(z = uvwxy\) 且:
- \(vwx\) 中的特异点个数小于等于 \(N\)
- \(vx\) 中的特异点个数大于等于 \(1\)
- \(uv^iwx^iy \in L\ (i = 0, 1, \dots)\)
设 CFL \(L\),不妨设 \(\varepsilon \notin L\),因此存在 CNF \(G = (V, T, P, S)\) 使得 \(L = L(G)\)。与泵引理的证明类似,取 \(N = 2^{|V| + 1}\)。
设 \(z \in L\),且 \(z\) 中的特异点数量不少于 \(N\)。现在构造一条从根结点到叶结点的路径 \(p\):
- 首先将根结点放入路径中
- 如果路径上的最后一个点只有一个儿子的后代中有特异点,则将这个儿子放入路径
- 如果路径上的最后一个点的两个儿子的后代中都有特异点,则将特异点多的那个儿子放入路径(相等则任取一个)
- 直到将叶子放入路径为止
定义分支点(branch point)为两个儿子的后代均有特异点的节点,则显然只有分支点会影响路径上特异点数量的变化。根据 \(p\) 的构造规则,可以发现路径上的每个分支点都有上个分支点至少一半的特异点。
由于在 \(z\) 中至少有 \(N\) 个特异点,因此在 \(p\) 的起点处(即根节点处)有至少 \(N\) 个特异点。又由于 \(p\) 每次经过分支点后都会保留超过一半的特异点数量,并且在叶子节点处的特异点数量为 \(0\),因此路径上至少有 \(|V| + 1\) 个分支点。
根据鸽巢原理,在这些分支点中至少有两个不同结点所对应的语法变量相同。类似泵引理的证明取 \(v_1, v_2\) 为最接近叶子的两个对应 \(A\) 的变量(不妨设 \(v_1\) 是 \(v_2\) 的祖先),可以令 \(z = uvwxy\) 对应 \(v_1, v_2\) 分隔出的叶子结点。
注意到路径 \(p\) 在 \(v_1\) 子树所包含的分支点数量小于等于 \(|V| + 1\),所以 \(v_1\) 的特异点数量之多为 \(N\)(即 \(vwx\) 中的特异点个数小于等于 \(N\))。由于 \(v_1, v_2\) 都是分支点,因此 \(vx\) 中至少包含一个特异点。
并且类似泵引理的证明,有 \(A \xRightarrow{*} v^iAx^i \xRightarrow{+} v^i w x^i\),因此有
\[S \xRightarrow{*} uAy \xRightarrow{+} uv^iAx^iy \xRightarrow{+} uv^iwx^iy\]
显然,只要标记每个点都是特异点,那么就可以从 Ogden 引理得到泵引理。也就是说 Ogden 引理是泵引理的推广。
应用
在下面的证明中,会使用下划线来标记特异点。
判定 CFL
在部分情况下泵引理可能无法证明一个语言不是 CFL,此时可以尝试使用 Ogden 引理来证明。
证明 \(L = \{a^n b^m c^k | n \ne m \wedge m \ne k \wedge k \ne n\}\) 不是 CFL。
首先不妨尝试使用泵引理来证明:设 \(N\) 为仅依赖于 \(L\) 的正整数,取
\[z = a^N b^{N + n} c^{N + m}\]
其中 \(n \ne m \wedge n \ne 0 \wedge m \ne 0\)。显然只要考虑 \(v, x\) 均为单字母组成的字符串的情况(其他情况 trivial)。
这里首先考虑 \(v = a^k, x = b^h\),只要令 \(k = h\) 那么 \(a, b\) 的数量永远不会相同。因此只要考虑 \(a, c\) 数量相同的情况,即 \(N + (i-1)k = N + m\) 的情况。由于 \(1 \le k \le N\) 是任取的,因此为了使得 \(i = m/k + 1\) 必定为整数,不妨令 \(m = N!\) 。因此取
\[z = a^N b^{N + N!} c^{N + 2N!}\]
取 \(v = a^k, x = b^h\),当 \(i = 2N!/k + 1\) 时,有
\[uv^iwx^iy = a^{N + 2N!} b^{N + N! + (2N!/k) h} c^{N + 2N!} \notin L\]
但是当 \(v = b^k, x = c^h\) 时用这种思路就无法找到矛盾了。这里需要用 Ogden 引理。
取 \(z = \underline{a^N} b^{N + N!} c^{N + 2N!}\),设 \(z = uvwxy\) 满足 Ogden 引理,那么 \(vx\) 中一定存在至少一个 \(a\),因此可能有三种情况:
- \(v\) 在 \(a\) 中,\(x\) 也在 \(a\) 中,\(N\) 与 \(2N!\) 奇偶性相同,因此取 \(i = 2N!/(k + h) + 1\ (k + h \le N)\) 即可
- \(v\) 在 \(a\) 中,\(x\) 在 \(b\) 中,已证明
- \(v\) 在 \(a\) 中,\(x\) 在 \(c\) 中,类似第二种情况,只不过让 \(a, b\) 的数量相同
判定固有二义性
下面这个例子来自于 Ogden 的论文。
证明 \(L = L_0 \cup L_1 = \{a^n b^m c^m | n, m \ge 1\} \cup \{a^m b^m c^n | n, m \ge 1\}\) 是固有二义的。
下用反证法证明 \(L\) 是固有二义的。
设 \(N\) 为 Ogden 引理中所描述的仅依赖于 \(L\) 的自然数。取 \(z = a^{N! + N} \underline{b^N c^N} \in L\)。根据 Ogden 引理,存在一个派生:
\[S \xRightarrow{*} uAy \xRightarrow{*} uvAxy \xRightarrow{*} uvwxy\]
其中 \(u = a^{N! + N} b^{N - s - k}, v = b^k, w = b^sc^{s’}, x = c^k, y = c^{N - s’ - k}\),满足 \(s + s’ \ge 1, k \ge 1, s + s’ + 2k \le N\)。
令 \(i = p!/k\),得到 \(uv^iwx^iy = a^{N + N!} b^{N + N!} c^{N + N!}\)。这个句子的派生方式为
\[S \xRightarrow{*} uAy \xRightarrow{*} uvAxy \xRightarrow{*} uv^2Ax^2y \xRightarrow{*} \dots \xRightarrow{*}uv^iwx^iy\]
此时在这棵派生树中 \(v^i w x^i = b^{p!+s}c^{p! + s’}\) 是树上某个代表 \(A\) 的结点的子树。
对于这个句子,如果标记 \(a^{N + N!} b^{N + N!}\) 则会得到 \(a^{p! + t} b^{p! + t’}\) 是树上某个结点的子树。由于 \((p! + s) + (p! + t’) \ge 2p! + 1 > p! + 1\),因此中间有一部分 \(b\) 在两种派生中的派生路径不同。
因此这个语言必定存在两棵不同的派生树,即 \(L\) 是固有二义的。
推广
Bader 和 Moura 推广了 Ogden 引理,加入了“排除点”:
定义 \(d\) 为句子中特异点的数量,定义 \(e\) 为句子中排除点的数量。
对于任意 CFL \(L\),存在仅依赖于 \(L\) 的一个正整数 \(N\),使得对于任意 \(z \in L\),如果在 \(z\) 中特异点和排除点数量满足 \(d \ge N(e + 1)\),则存在 \(u, v, w, x, y\) 使得 \(z = uvwxy\) 且:
- \(vwx\) 中的特异点个数小于等于 \(N^{e + 1}\)
- \(vx\) 中的特异点个数大于等于 \(1\),且没有排除点
- \(uv^iwx^iy \in L\ (i = 0, 1, \dots)\)
Parihk 定理
Parihk 定理的证明
Parihk 定理表明对于一个 CFL,如果我们只关心其中每个字母出现的次数而不关心顺序,那么这个 CFL 可以对应到一个 RL。
(Parikh Vector)
设字母表 \(\Sigma = \{a_1, a_2, \dots, a_k\}\),定义一个句子 \(w\) 的 parihk vector 为
\[p : \Sigma^* \rightarrow \mathbb{N}^k \overset{\text{def}}{=} p(w) = (|w|_{a_1}, |w|_{a_2}, \dots, |w|_{a_k})\]
其中 \(|w|_{a_i}\) 表示 \(a_i\) 在 \(w\) 中出现的次数。
(Linear and Semilinear)
定义线性(linear)集合 \(u\) 满足 \(\exists u_0, u_1, \dots, u_k. u = \{u_0 + t_1 u_1 + \dots + t_k u_k | t_1, t_2, \dots, t_k \in \mathbb{N} \}\),或者写作 \(u = u_0 + \{u_1, u_2, \dots, u_k\}^{*}\)。
定义半线性(semilinear)集合 \(u\) 满足 \(\exists u_0, u_1, \dots, u_k. u = u_1 \cup u_2 \cup \dots u_k \),其中 \(u_i\ (1 \le i \le k)\) 是线性集合。根据定义,有限个半线性集合的并仍然是半线性集合。
显然任何的 parihk vector 都可以表示成基向量(单字母对应的 parihk vector)的线性组合。
在描述 parihk’s theorem 前,需要证明一个泵引理的增强形式:
设 CFL \(L\),考虑对应的 CNF \(G\) 且 \(L(G) = L\)。存在 \(N \ge 1\),对于任意 \(k \ge 1\),对于任意 \(z \in L\) 且 \(|z| \ge N^k\),存在 \(u, x_1, \dots, x_k, w, y_k, \dots, y_1, v\) 使得 \(z = u x_1 x_2 \dots x_k w y_k y_{k-1} \dots y_1 v\) 满足
- \(|x_1 x_2 \dots x_k w y_k y_{k-1} \dots y_1| \le N^k\)
- \(|x_i y_i| \ge 1\)
- \(\exists A \in V. S \xRightarrow{*} uAv; A \xRightarrow{*} w | x_1 A y_1 | x_2 A y_2 | \dots | x_k A y_k\)
由于 \(|z| \ge N^k\) 因此派生树上存在一条长度大于 \(k|V| + 1\) 的路径。
类似泵引理的证明,根据鸽巢原理,路径上有 \(k + 1\) 个相同的语法变量,即语法变量 \(A\)。
(Parihk’s Theorem)
设 CFL \(L\),令 \(P(L)\) 为 \(L\) 中句子对应的 parihk vectors 组成的集合(即 \(P(L) = \{p(w) | w \in L\}\)),则 \(P(L)\) 是半线性集合。
如果 \(S\) 是一个半线性集合,那么存在一个 RL \(L’\),其 parihk vector \(P(L’) = S\)。
Parihk 定理的证明分为两个部分。
首先证明第一部分。设 CFL \(L\),对应 CNF \(G\) 且 \(L(G) = L\)。
设 \(U \subseteq V\),定义 \(L_U \subseteq L\),其中 \(\forall w \in L_U\),存在一个推导 \(S \xRightarrow{*} w\) 使用且仅使用了 \(U\) 中的所有语法变量。
显然有 \(L = \cup_U L_U\)。因此只要证明 \(p(L_U)\) 是一个半线性集合。定义 \(\xRightarrow[\subseteq U]{*}\) 表示推导中只使用了 \(U\) 中的语法变量(可以有没使用的)。对于某个 \(U \in V\),可以构建两个有限集合 \(F, G\) 使得 \(p(L_U) = p(F G^*)\):
\[F = \{w \in L_U \vert |w| < N^k\}\]
\[G = \{xy | 1 \le |xy| \le N^k \wedge \exists A \in U. A \xRightarrow[\subseteq U]{*} xAy\}\]
首先证明 \(p(L_U) \subseteq p(F G^{*})\),取 \(w \in L_U\),对 \(|w|\) 进行归纳
如果 \(|w| < N^k\),那么 \(w \in F\),即 \(p(w) \in p(F G^*)\) 成立
否则,由增强的泵引理知 \(\exists A \in V.\)
\begin{aligned} S & \xRightarrow[d_0]{*} uAv \xRightarrow[d_1]{*} u x_1 A y_1 v \xRightarrow[d_2]{*} u x_1 x_2 A y_2 y_1 v \xRightarrow[d_3]{*} \dots \\ & \xRightarrow[d_k]{*} u x_1 \dots x_k A y_k \dots y_1 v \xRightarrow[d_{k+1}]{*} u x_1 \dots x_k w y_k \dots y_1 v \end{aligned}
根据定义有 \(A \in U\),因此 \(U ∖ \{A\} \) 中共有 \(k - 1\) 个元素。而在上面的推导 \(d_1, d_2, \dots, d_k\) 一共有 \(k\) 次,因此有一个变量在这里至少被推出了两次,不妨设是 \(d_i, d_j\)。因此可以将 \(A \xRightarrow[d_i]{*} x_i A y_i\) 从中删掉,得到 \(w’\),且仍然可以保证满足 \(L_U\) 的定义。
\[p(w) = p(uzv) + \sum_{i=1}^k p(x_i y_i) = p(w’) + p(x_i y_i)\]
根据归纳假设知 \(p(w’) \in p(F G^*)\),且根据定义有 \(x_i y_i \in G\),所以 \(p(w) \in p(F G^*)\)。
下面证明 \(p(FG^*) \subset p(L_U)\),对取 \(w \in FG^*\),对 \(|w|\) 进行归纳:
- 当 \(|w| < N^k\) 时,\(w \in F \subset L_U\),即 \(p(w) \subset p(L_U)\)
- 否则令 \(w = FG^*G = w’ x y \ (w’ \in FG^* \wedge xy \in G)\)。根据归纳假设,\(p(w’) \subset p(L_U)\),且 \(\exists A \in U. A \xRightarrow[\subseteq U]{*} xAy\)。因此 \(p(w’) + p(xy) \subset p(L_U)\) 仍然成立。
综上,第一部分证明完成
第二部分的证明较为简单:首先空集和单字母都是 RL;如果 \(u_i\ (0 \le i \le k)\) 都能表示成 RL,那么对于线性集合 \(u = \{u_0 + t_1 u_1 + \dots + t_k u_k | t_1, t_2, \dots, t_k \in \mathbb{N} \}\),其对应的 RL 为 \(\{u_0\} (u_1 | u_2 | \dots | u_k)^*\)。归纳知所有的线性集合都可以表示成 RL。由于 RL 对于并操作封闭,且半线性集合是线性集合的并,因此半线性集合也存在对应的 RL。
推论
单字母表(\(|\Sigma| = 1\))上的 CFL 一定是 RL。
根据 Parihk theorem,对于 CFL \(L\) 一定存在 RL \(L’\) 与之对应。由于 \(L\) 中所有字母相同,因此 \(L = L’\)。所以 \(L\) 也是 RL。
如果一个语言与另个语言的 parihk vector 相同,而后者不是 RL,那么前者也不可能是 CFL。
例如证明 \(L = \{a^n | \text{$n$ is a prime}\}\) 不是 CFL,根据推论有 \(L\) 一定是 RL。而这一点在前面证明了是不成立的,因此 \(L\) 一定也不是 CFL。
判定性质
Emptiness problem
判定一个 CFL 是否为空。
首先去除所有无用符号。如果起始符号是无用符号,那么语言为空。
Membership problem (CYK)
一般使用 CYK 算法判定一个句子是否属于一个 CFL,其复杂度为 \(O(n^3 |P|)\) ,思想是区间 DP。
\begin{algorithm} \caption{Membership check} \begin{algorithmic} \procedure{CYK}{CNF $G = (V, T, P, S)$, the string to be checked $x \in T^{*}$} \state set $n$ to be the length of $x$ \state \comment{$V_{i, j}$ represents a set of grammar variables that can derive to $x_{i, j}$} \state set every element in $V_{1 \dots n, 1 \dots n}$ to be $\emptyset$ \for {$c \in x$} \state $V_{i, i} \gets \{A | A \rightarrow x_{i, i} \in P\}$ \endfor
\for {$k \in 2 \dots n$}
\for {$l \in 1 \dots n - k + 1$}
\state $r \gets l + k - 1$ \state \comment{compute $V_{l, r}$} \for {$i \in l \dots r - 1$} \state $V_{l, r} \gets V_{l, r} \cup \{ A | A \rightarrow BC \in P \wedge B \in V_{l, i} \wedge C \in V_{i + 1, r} \}$ \endfor \endfor \endfor \endprocedure \end{algorithmic} \end{algorithm}
Inifinitiness problem
判定一个 CFL 是否为无穷语言。
设 CFL \(L\) 对应的文法为 \(G\),首先去除 \(G\) 的无用符号,然后用一张有向图来表示 \(G\):图的顶点为 \(G\) 中的语法变量,如果 \(A \rightarrow \alpha B \beta\),那么在图中增加一条从 \(A\) 到 \(B\) 的边。图的源点为 \(S\)。
最终,如果图中存在可以从源点到达的环,那么这个 CFL 是一个无穷语言。
封闭性
对并,拼接,闭包,翻转封闭
CFL 对并、拼接、闭包、翻转封闭。
设 CFL \(L_1, L_2\),对应的 CFG 为 \(G_1(V_1, T_1, P_1, S_1), G_2(V_2, T_2, P_2, S_2)\)。
由于可以重命名,因此不妨设 \(V_1 \cap V_2 \ne \emptyset\)。
取
\[G_3 = (V_1 \cup V_2 \cup \{S_3\}, T_1 \cup T_2, P_1 \cup P_2 \cup \{S_3 \rightarrow S_1 | S_2\}, S_3)\]
\[G_4 = (V_1 \cup V_2 \cup \{S_4\}, T_1 \cup T_2, P_1 \cup P_2 \cup \{S_4 \rightarrow S_1 S_2\}, S_4)\]
\[G_5 = (V_1 \cup \{S_5\}, T_1, P_1 \cup \{S_5 \rightarrow S_5 S_0 | \varepsilon\}, S_5)\]
\[G_6 = (V_1’ \cup \{S_0’\}, T_1, \{\alpha_i’ \rightarrow \beta_n’ \beta_{n-1}’ \dots \beta_1’ | \alpha_i \rightarrow \beta_1 \beta_2 \dots \beta_n \in P_1\}, S_0’)\]
则它们分别对应 \(L_1 \cup L_2\),\(L_1 L_2\),\(L_1^*\) 和 \(L_1^R\)。
对交,补,差不封闭
CFL 对交运算不封闭。
设 \(L_1 = \{0^n 1^n 2^m | n, m \ge 1\}, L_2 = \{0^n 1^m 2^m | n, m \ge 1\}\),那么 \(L_1 \cap L_2 = \{0^n 1^n 2^n | n \ge 1\}\),显然这不是一个 CFL。
CFL 对补运算和差运算不封闭。
\(L_1 \cap L_2 = \overline{\overline{L_1} \cup \overline{L_2}}\),由于 CFL 对并运算封闭但是对交运算不封闭,因此可以推出 CFL 对补运算也不封闭。
\(L_1 \cup L_2 = L_1 - (L_1 - L_2)\),同理 CFL 对差运算也不封闭。
CFL 与 RL
尽管 CFL 和 CFL 的交不一定是 CFL,但是 CFL 与 RL 的交依然是 CFL。
CFL 与 RL 的交仍然是 CFL。
考虑 CFL \(L_1\) 和 RL \(L_2\),并且
PDA \(M_1 = (Q_1, \Sigma, \Gamma, \delta_1, q_{01}, Z_0, F_1)\)
DFA \(M_2 = (Q_2, \Sigma, \delta_2, q_{02}, F_2)\)
使得 \(L_1 = L(M_1), L_2 = L(M_2)\)。令 PDA
\(M = (Q_1 \times Q_2, \Sigma, \Gamma, \delta, [q_{01}, q_{02}], Z_0, F_1 \times F_2)\)
其中 \(\forall([q, p], a, Z) \in (Q_1 \times Q_2) \times \Sigma \times \Gamma.\)
\[\delta([q, p], a, Z) = \{([q’, p’], \gamma) | (q’, \gamma) \in \delta_1(q, a, Z) \wedge p’ = \delta(p, a)\}\]
\[\delta([q, p], \varepsilon, Z) = \{([q’, p’], \gamma) | (q’, \gamma) \in \delta_1(q, \varepsilon, Z)\}\]
不难发现 \(\forall x \in \Sigma^*. x \in (L(M_1) \cap L(M_2)) \iff x \in L(M)\)。
CFL 与 RL 的差仍然是 CFL。
\[L - R = L \cap \overline{R}\]
但是 RL - CFL 不是 CFL:
RL 与 CFL 的差不一定是 CFL。
\[B = \{ a^*b^*c^* \}\] \[A_1 = \{ a^i b^j c^* | i > j \}\] \[A_2 = \{ a^i b^j c^* | i < j \}\] \[A_3 = \{ a^*b^i c^j | i > j \}\] \[A_4 = \{ a^*b^i c^j | i < j \}\] \[A = A_1 \cup A_2 \cup A_3 \cup A_4\]
显然 \(A_1 \dots A_4\) 都是 CFL,因此 \(A\) 也是 CFL;且 \(B\) 是 RL。
然而 \(B - A = \{a^i b^i c^i\}\) 不是 CFL。
同态映射
(代换)
设 CFG \(G = (V, T, P, S)\),代换 \(f : T \rightarrow 2^{\Sigma^*}\) 满足 \(\forall a \in T\),\(f(a)\) 是 \(\Sigma\) 上的 CFL。
类似的,代换的定义可以扩展到整个语言上。
CFL 在代换下封闭。
设 CFL \(L\),CFG \(G = (V, T, P, S)\) 满足 L = L(G)。
设 \(\forall a \in T\),\(f(a)\) 是 \(\Sigma\) 上的 CFL。记 CFG \(G_a = (V_a, \Sigma, P_a, S_a)\) 且 \(f(a) = L(G_a)\)。为了方便起见不妨设 \(\forall a, b \in T. a \ne b \iff V_a \cap V_b = \emptyset \wedge V_a \cap V = \emptyset\)。
取 CFG
\[G’ = \{V \cup \bigcup_{a \in T} V_a, \Sigma, P’ \cup \bigcup_{a \in T} P_a, S\}\]
\[P’ = \left \{A \rightarrow A_1 A_2 \dots A_n | A \rightarrow X_1 X_2 \dots X_n \in P \wedge \left (A_i = \begin{cases} X_i, &X_i \in V \\ S_{X_i}, & \operatorname{\mathrm{else}} \end{cases} \right) \right \}\]
首先证明 \(L(G’) \subseteq f(L)\),设 \(x \in L(G’)\),则
\begin{aligned} S & \xRightarrow[G’]{*} S_{a_1} S_{a_2} \dots S_{a_n} \\ & \xRightarrow[G’]{+} x_1 S_{a_2} \dots S_{a_n} \\ & \xRightarrow[G’]{+} x_1 x_2 \dots S_{a_n} \\ & \dots \\ & \xRightarrow[G’]{+} x_1 x_2 \dots x_n = x \end{aligned}
其中 \(S_{a_i} \xRightarrow[G’]{*} x_i\)。又由于 \(S_{a_i} \xRightarrow[G’]{*} x_i \iff S_{a_i} \xRightarrow[G_{a_i}]{*} x_i\),则 \(S_{a_i} \xRightarrow[G_{a_i}]{*} x_i\),即 \(x_i \in L(G_{a_i}) = f(a_i)\)。
由定义知 \(S \xRightarrow[G’]{*} S_{a_1} S_{a_2} \dots S_{a_n} \iff S \xRightarrow[G]{*} a_1 a_2 \dots a_n\),因此 \(a_1 a_2 \dots a_n \in L\)。
所以
\[x = x_1 x_2 \dots x_n \in f(a_1) f(a_2) \dots f(a_n) = f(a_1 a_2 \dots a_n) \subseteq f(L) \]
即 \(x \in f(L)\) 成立。类似的,反向也可以这样证明。
由于同态映射是代换的特例,因此有:
CFL 的同态像是 CFL。
下面证明对于同态原像也有类似的定理:
CFL 的同态原像是 CFL。
设 L 是 \(\Sigma_2\) 上的 CFL,同态映射 \(f : \Sigma_1^* \rightarrow \Sigma_2^*\),下面证明 \(f^{-1}(L)\) 是 CFL。
任取 \(a = a_1 a_2 \dots a_n \in \Sigma_1^*\),设 \(f(a_i) = x_i\),且 \(x = x_1 x_2 \dots x_n\)。根据定义有 \(a \in f^{-1}(L) \iff x = f(a) \in L\)。因此我们需要构造这样两个 PDA,当 \(M_1\) 在处理 \(a_i\) 时,\(M_2\) 同时在处理 \(x_i\)(其中 \(a_i\) 是字符而 \(x_i\) 是字符串)。当 \(M_2\) 处理完 \(x_i\) 后,\(M_1\) 再读入下一个字符,为此需要记录 \(M_2\) 当前读了多少字符。由于 \(a \in \Sigma_1\) 是有穷的,且 \(f(a)\) 是有穷的,因此可以将其记录在状态中。
设 \(M_2 = (Q_2, \Sigma_2, \Gamma, \delta_2, q_0, Z_0, F)\) 且 \(L(M_2) = L\),定义:
\(M_1 = (Q_1, \Sigma_1, \Gamma, \delta_1, [q_0, \varepsilon], Z_0, F \times \{\varepsilon\})\)
其中
\[Q_1 = \{[q, x] | q \in Q_2 \wedge \exists a \in \Sigma_1. x = f(a)[i \dots]\}\]
此处 \(x=f(a)[i \dots]\) 表示 \(x\) 是 \(f(a)\) 的一个后缀。状态 \([q, x]\) 表示目前 \(M_2\) 在状态 \(q\),当前步骤还剩下 \(x\) 没读完。
\(\delta_1\) 的定义如下:
- 对于 \(a \in \Sigma_1\),直接将 \(f(a)\) 放入状态:\(\forall (q, a, A) \in Q_2 \times \Sigma_1 \times \Gamma. \delta_1([q, \varepsilon], a, A) \ni ([q, f(a)], A)\)
- 在 \(M_1\) 下用 \(\varepsilon\) 移动模拟 \(M_2\) 读取 \(f(a)\):\(\delta_2(q, a, A) \ni (p, \gamma) \Rightarrow \delta_1([q, ax], \varepsilon, A) \ni ([p, x], \gamma)\)
- 在 \(M_1\) 下用 \(\varepsilon\) 移动模拟 \(M_2\) 读取 \(\varepsilon\):\(\delta_2(q, \varepsilon, A) \ni (p, \gamma) \Rightarrow \delta_1([q, ax], \varepsilon, A) \ni ([p, x], \gamma)\)
下面证明 \(L(M_1) = f^{-1}(L(M_2))\),为此先证 \(L(M_1) \subseteq f^{-1}(L(M_2))\)。
设 \(x \in L(M_1)\) 且 \(x = x_1 x_2 \dots x_n\)。根据定义,存在 \(q_1, q_2, \dots, q_n \in Q_2\) 满足
\[([q_0, \varepsilon], x_1 x_2 \dots x_n, Z_0) \vdash_{M_1} ([q_0, f(x_1)], x_2 \dots x_n, Z_0)\]
\[([q_0, f(x_1)], x_2 \dots x_n, Z_0) \vdash_{M_1}^* ([q_1, \varepsilon], x_2 \dots x_n, \gamma_1)\]
\[([q_1, \varepsilon], x_2 \dots x_n, \gamma_1) \vdash_{M_1} ([q_1, f(x_2)], x_3 \dots x_n, \gamma_1)\]
\[\dots\]
\[([q_{n-1}, f(x_n)], \varepsilon, \gamma_{n-1}) \vdash_{M_1}^* ([q_n, \varepsilon], \varepsilon, \gamma_n)\]
根据 \(M_1\) 的定义,有
\[(q_0, f(x_1) f(x_2) \dots f(x_n), Z_0) \vdash_{M_2}^* (q_1, f(x_2) \dots f(x_n), \gamma_1)\]
\[(q_1, f(x_2) \dots f(x_n), \gamma_1) \vdash_{M_2}^* (q_1, f(x_3) \dots f(x_n), \gamma_3)\]
\[\dots\]
\[(q_{n-1}, f(x_n), \gamma_{n-1}) \vdash_{M_2}^* (q_n, \varepsilon, \gamma_n)\]
因此 \(f(x_1) f(x_2) \dots f(x_n) \in L(M_2)\)。又由于 \(x_1 x_2 \dots x_n \in f^{-1}(L(M))\),因此 \(L(M_1) \subseteq f^{-1}(L(M_2))\) 成立。
类似可以证明 \(f^{-1}(L(M_2)) \subseteq L(M_1)\)。
综上,定理得证。
DCFL
DCFL 对补封闭
设 DCFL \(L\),以终态接收的 DPDA \(M\) 满足 \(L = L(M)\)。
考虑 \(\Sigma^* - L\) 一个简单的想法是为 DPDA 中状态机的部分取反,这使得 \(L\) 中的句子会被拒绝,并且大部分 \(\Sigma^* - L\) 的句子会被接收。但是这还有两个问题:
- 对于 \(w \notin L\),有可能 \(M\) 在没有读完 \(w\) 时没有下一个动作(例如栈空了)导致无法接收;那么在新自动机中依然无法接收 \(w\)
- \(M\) 中可能存在 \(\varepsilon\) 转移
- 对于 \(w \notin L\),在 \(M\) 可以通过 \(\varepsilon\) 使其在 DPDA 内无限循环从而不接收它;那么在新自动机中 \(w\) 仍然会无限循环,仍然无法接收
- 对于 \(w \in L\),这使得 \(M\) 可以先在非终止状态读完 \(w\) 然后用一个 \(\varepsilon\) 转移到终止状态;那么在新自动机中仍然会接受 \(w\)
下面首先解决第一个问题和第二个问题的第一部分:
- 对于第一个问题
- 在栈底增加一个符号(\(Z_0’\))避免读至空栈无法接收的情况
- 补充状态机的陷阱状态(\(d\))
- 对于第二个问题,用类似 \(\varepsilon\)-NFA 到 NFA 的思路,消除 \(\varepsilon\) 移动
- 对于无限循环直接 stuck
- 否则,增加一个状态 \(f\) 作为最终状态:到达 \(f\) 时如果读完则接收,否则 stuck
对于任意 DPDA \(M\) 存在一个与 \(M\) 等价的 DPDA \(M’\) 使得 \(\forall w \in \Sigma^*. M’\) 都能读完 \(w\)。
设 DPDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, Z_0, F)\)。
令 DPDA \(M’ = (Q \cup \{q_0’, d, f\}, \Sigma, \Gamma \cup \{Z_0’\}, \delta_0’, q_0’, Z_0’, F \cup \{f\})\),其中:
\(\delta’(q_0’, \varepsilon, Z_0’) = \{(q_0, Z_0 Z_0’)\}\)
处理读不完 stuck 的情况:
\[\forall q \in Q, a \in \Sigma, Z \in \Gamma. \delta(q, a, Z) = \emptyset \wedge \delta(q, \varepsilon, Z) = \emptyset \rightarrow \delta’(q, a, Z) = \{(d, Z)\} \]
如果一个状态后续只有 \(\varepsilon\) 转移,即对于 \(q \in Q, Z \in \Gamma. \forall i \in \mathbb{N}. (q, \varepsilon, Z) \xRightarrow[M]{i} (q_i, \varepsilon, \gamma_i)\):
如果这导致无限循环并无法终止,则令其 stuck,即:
\[\forall i \in \mathbb{N}. q_i \notin F \rightarrow \delta’(q, \varepsilon, Z) = \{(d, Z)\}\]
否则,若它可以终止,那么它可能会导致第二个问题的第一种情况。这里使用一个特殊的状态 \(f\)
\[\exists i \in \mathbb{N}. q_i \in F \rightarrow \delta’(q, \varepsilon, Z) = \{(f, Z)\}\]
根据定义,如果此时已经读完 \(w\),由于已进入接受状态 \(f\),因此 \(w\) 会被接受;否则 \(w\) 不会被 \(M\) 接收,\(M’\) 会进入 \((d, Z)\)(见下面的陷阱状态处理)
\(\forall q \in Q, a \in \Sigma \cup \{\varepsilon\}, Z \in \Gamma.\) 如果 \(\delta’(q, a, Z)\) 没有被上面的步骤定义,那么 \(\delta’(q, a, Z) = \delta(q, a, Z)\)
最后是陷阱状态的处理:
- \(\forall a \in \Sigma, Z \in \Gamma \cup \{Z_0’\}. \delta’(d, a, Z) = \{(d, Z)\}\)
- \(\forall Z \in \Gamma \cup \{Z_0’\}. \delta’(f, \varepsilon, Z) = (d, Z)\)
最后考虑处理第二个问题的第二种情况,需要记录当前状态是不是刚从终态通过 \(\varepsilon\) 转移出来。
DCFL 对补运算封闭。
对于给定的 DFCL \(L\),设对应的 DPDA 为 \(M\),那么根据上面的 lemma 存在一个与 \(M\) 等价的 DPDA \(M’ = \{Q, \Sigma, \Gamma, \delta, q_0, Z_0, F\}\) 使得 \(\forall w \in \Sigma^*\),\(M’\) 都能读完 \(w\)。
构造 \(M’’ = (Q’, \Sigma, \Gamma, \delta’, q_0’, Z_0, F’)\),其中:
- \(Q’ = \{[q, k] | q \in Q, k \in \{1, 2, 3\}\}\)
- \(F’ = \{[q, 3] | q \in Q\}\)
- \(q_0’ = \begin{cases} [q_0, 1], &q_0 \in F \\ [q_0, 2], &q_0 \notin F \end{cases}\)
此处 \(k = 1\) 表示 \(M’\) 正处于终态或刚从终态通过 \(\varepsilon\) 移动转出;\(k = 2\) 是普通状态;\(k = 3\) 是 \(M’’\) 的真正终态。
如果 \(\delta(q, \varepsilon, Z) = (p, \gamma)\),对于 \(k = 1 \vee 2\)
\[\delta’([q, k], \varepsilon, Z) = \begin{cases} \{([p, 1], \gamma)\}, & k = 1 \vee p \in F \\ \{([p, 2], \gamma)\}, & \text{else} \end{cases}\]
如果 \(\delta(q, a, Z) = (p, \gamma)\)
对于非终态允许取反接受:
\[\delta’([q, 2], \varepsilon, Z) = \{([q, 3], Z)\}\]
对于特殊状态,考虑要不要返回普通状态
\[\delta’([q, 1], a, Z) = \delta’([q, 3], a, Z) = \begin{cases} \{([p, 1], \gamma)\}, & p \in F \\ \{([p, 2], \gamma)\}, & p \notin F \\ \end{cases}\]
这里的 \(\varepsilon\) 转移隐含了 \(([q, 2], ax, Z) \vdash_{M’’} ([q, 3], ax, Z) \vdash_{M’’} \begin{cases} ([p, 1], x, \gamma), & p \in F \\ ([p, 2], x, \gamma), & p \notin F \\ \end{cases}\)。也就是说 \(M’’\) 在读入一个字符后行为是一致的,只需要考虑 \(M’\) 会不会转移到终态。
显然 \(M’’\) 是 DPDA。
下面证明 \(L(M’’)\) 是 \(L(M’)\)(即 \(L(M’’)\))的补集。
- 设 \(w = a_1 a_2 \dots a_n \in L(M’)\),\(M’\) 读完 \(a_n\) 后经过数步必然会进入到某一终态 \(q\),即 \((p, a_n, Z) \vdash_{M’}^* (q, \varepsilon, \gamma)\)。不妨设 \(q\) 是 \(M’\) 遇到的第一个终态
- 读完 \(a_n\) 后,在遇到终态前,\(M’\) 可能会先经过一串 \(\varepsilon\) 转移;遇到终态后,也会经过一串 \(\varepsilon\) 转移
- 根据定义,\(M’’\) 读完 \(a_n\) 后处于 \([p’, 2]\)(因为后面的 \(q\) 才是第一个遇到的终态,\(M’\) 还处于非终态);然后经过一串 \(\varepsilon\) 转移。这个过程中 \(k\) 保持不变,直到遇到终态 \(q\)
- 遇到终态 \(q\) 后 \(k = 1\)
- 在经过 \(q\) 之后只有 \(\varepsilon\) 转移,因此一直有 \(k = 1\),所以 \(M’’\) 不会接受 \(w\)
- 设 \(w = a_1 a_2 \dots a_n \notin L(M’)\)
- 读完 \(a_n\) 后,\(M’\) 可能会先经过一串 \(\varepsilon\) 转移
- \(M’\) 读完 \(a_n\) 后一定在非终态,根据分析此时 \(M’’\) 处于 \([p, 2]\)
- 其后会经历一串 \(\varepsilon\) 转移,根据定义始终有 \(k = 2\)
- 结束时处于 \([q, 2]\) 此时通过一个 \(\varepsilon\) 转移即得到 \([q, 3]\)。因此 \(M’’\) 可以接收 \(w\)
综上,\(L(M’’)\) 就是 \(L(M)\) 的补集。同时由于 \(M’’\) 是 DPDA,因此 DCFL 的补集也是 DCFL。
对每个 DCFL \(L\) 都存在一个 DPDA \(M\) 接受 \(L\) 并且
\[\forall q \in F, x \in \Gamma. \delta(q, \varepsilon, x) = \emptyset\]
上面构造的 \(M’’\) 满足 \(\forall q \in Q. \delta’([q, 3], \varepsilon, Z) = \emptyset\)。
因此只要构造其补集 \(M’’’\) 则 \(L(M’’’) = L(M)\) 且满足条件。
DCFL 与 NCFL
下面证明 \(L = \{a^ib^jc^k | i \ne j \vee j \ne k\}\) 不是 DCFL。其 CFG 非常好构造,考虑原语言等价于 \(\{a^ib^jc^k | i > j \vee i < j \vee j > k \vee j < k\}\),后者显然可以构造 CFG,因此 \(L\) 是 CFL。
下面用反证法证明 \(L\) 不是 DCFL:
- 假设 \(L\) 是 DCFL,那么它对补集封闭
- 则其补集 \(L’ = \{a^ib^jc^k | i = j = k \ge 0\} \cup \{(a|b|c)^* | a, b, c \text{ are unordered}\}\) 也是 DCFL,同时也是一个 CFL
- 那么 \(L’’ = L’ \cap (a*b*c*) = \{a^ib^jc^k | i = j = k \ge 0\}\) 也是一个 CFL
- 显然这并不成立,因此 \(L\) 不是 DCFL。
即存在是 CFL 但不是 DCFL 的语言。
DCFL 对并,交不封闭
DCFL 对并运算不封闭。
- \(L_1 = \{a^i b^i c^k | i, k \ge 0\}\)
- \(L_2 = \{a^i b^k c^k | i, k \ge 0\}\)
- \(L_3 = L_1 \cup L_2 = \{a^i b^j c^k | i \ne j \vee j \ne k\}\)
前面已经证明 \(L_3\) 不是 DCFL。
DCFL 对交运算不封闭。
取:
- \(L_1 = \{a^i b^i c^k | i, k \ge 0\}\)
- \(L_2 = \{a^i b^k c^k | i, k \ge 0\}\)
- \(L_3 = L_1 \cap L_2 = \{a^n b^n c^n | n \ge 0\}\)
显然 \(L_1, L_2\) 都是 DCFL,但是 \(L_3\) 不是 CFL。
CFL 的层次结构
CFL \(\rightarrow\) 非固有二义 CFL \(\rightarrow\) DCFL \(\rightarrow\) RL