[形式语言] 03 Regular Expression and Regular Language

为了证明这个问题，只需要证明对于任意正则表达式，存在一个 $\varepsilon$-NFA 与之等价；且对于任意 DFA，存在一个正则表达式与之等价。

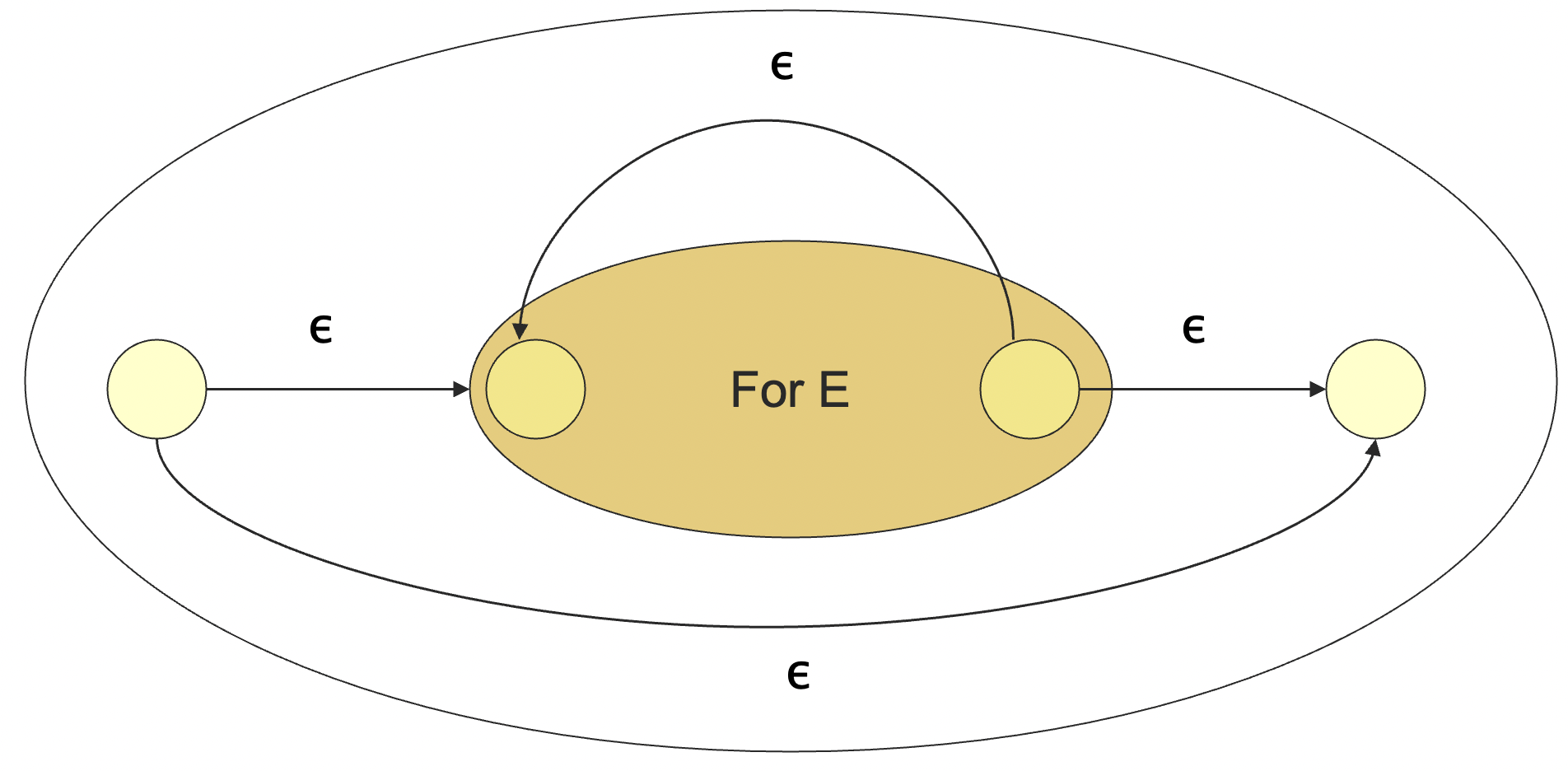
• 对于任意正则表达式，存在一个 $\varepsilon$-NFA 与之等价

  只要根据正则表达式的构建树，按照下面的规则进行转换即可。

• 对于任意 DFA 存在一个正则表达式与之等价

  首先对 DFA $M = (Q, \Sigma, \delta, q_0, F)$ 上的结点进行标号：$1, 2, \dots, n$。

  定义一条 $k$-路径为 DFA 上的一条路径，其中路径上的点（不包括起点和终点）的标号不超过 $k$。因此所有路径都是 $n$-路径。路径上的边构成了一个句子。

  记 $R^k_{ij}$ 为点 $i$ 到点 $j$ 的所有 $k$-路径组成的语言，下面开始构造 $R^k_{ij}$。

  • 当 $k=0$ 时

    • 如果 $i = j$，则 $R^0_{ii} = \varepsilon + a_1 + a_2 + \dots + a_n (\delta(i, a_l) = i)$
    • 如果 $i \ne j$，且不存在从 $i$ 到 $j$ 的路径，则 $R^0_{ij} = \emptyset$
    • 如果 $i \ne j$，且存在从 $i$ 到 $j$ 的路径，则 $R^0_{ij} = a_1 + a_2 + \dots + a_n (\delta(i, a_l) = j)$

  • 当 $k > 0$ 时，假设所有 $k-1$-路径都可以转换成正则表达式

    • 则从 $i$ 到 $j$ 的路径有两种选择：不经过 $k$ 或至少经过 $k$ 一次
    • 因此 $R^k_{ij} = R^{k-1}_{ij} + R^{k-1}_{ik} (R^k_{kk})^{*} R^{k-1}_{kj}$

    根据这个方法可以构造出 $R^n_{q_0 q_f} (q_f \in F)$，此时 $R^n_{q_0q_{f1}} + R^n_{q_0q_{f2}} + \dots + R^n_{q_0q_{fm}} (f_i \in F)$ 即是答案。

设 RL $L$，DFA $M = (Q, \Sigma, \delta, q_0, F)$ 满足 $L(M) = L, |Q| = N$。为方便起见，不妨设 $M$ 中不含不可达状态。

取 $z = a_1 a_2 \dots a_m \in L (m \ge N)$，记 $z$ 在 $M$ 上经过的状态为 $q_h = \delta(q_0, a_1 a_2 \dots a_h) (1 \le h \le m)$。

由于 $m \ge N$，因此存在 $q_i, q_j \in Q (1 < i < j < m = N)$ 使得 $q_i = q_j$。即

$$\delta(q_0, a_1 a_2 \dots a_i) = q_i$$ $$\delta(q_0, a_1 a_2 \dots a_j) = q_j = q_i$$

因此 $\forall k \ge 0, \delta(q_i, (a_{i+1} a_{i+2} \dots a_j)^k = q_j = q_i)$

因此，

$$\forall k \ge 0, \delta(q_0, a_1 a_2 \dots a_i (a_{i+1} a_{i+2} \dots a_j)^k a_{j + 1} \dots a_m) = a_m$$

取 $u = a_1 a_2 \dots a_i, v = a_{i+1} a_{i+2} \dots a_j, w = a_{j+1} a_{j+2} \dots a_m$

则 $\forall i \ge 0$ 有

• $|uv| \le N$
• $|v| \ge 1$

设 $L$ 是 RL，则 $L$ 满足 pumping lemma。

设 $n$ 是仅依赖于 $L$ 的正整数，取 $z = 0^{n + p} \in L$，其中 $n + p$ 是素数。由 pumping lemma 知存在 $z = uvw$ 满足条件。由于 $|v| \ge 1$，不妨设 $v = 0^k$，$u = 0^{n - k}$。且 $\forall i \ge 0, uv^iw = 0^{n - k + ik + p} = 0^{n + p + (i - 1)k}$。

当 $i = n + p + 1$ 时，$uv^iw = 0^{(n + p)(k + 1)}$ 非素数，矛盾，因此原命题不成立。

下面通过证明 $(1) \rightarrow (2) \rightarrow (3) \rightarrow(1)$ 来证明。

• $(1) \rightarrow (2)$

  设 $L \subseteq \Sigma^*$ 是 RL，则存在 DFA $M(Q, \Sigma, \delta, q_0, F)$ 使得 $L(M) = L$。令关系 $R = R_M$。

  • 由前面的定义知 $R_M$ 是 $\Sigma^*$ 上的右不变等价关系
  • 由 $|\Sigma^* / R_M| \le |Q|$，所以 $R_M$ 具有有穷指数
  • 如果 $x \in L$，那么 $\delta(q_0, x) = t \in F$。因此 $\forall x \in L, x \in \mathrm{set}(t) (t \in F)$，所以 $L = \cup_{t \in F}(\mathrm{set}(t))$ 即 $L$ 是 $R$ 的某些等价类的并

• $(2) \rightarrow (3)$，因此需要证明 $R$ 是 $R_L$ 的加细，即需要证明 $\forall x, y \in \Sigma^*. x R y \rightarrow x R_L y$

  由于 $R$ 是右不变的，所以 $\forall z \in \Sigma^*. xz R yz$。

  又由于 $L$ 是 $R$ 的部分等价类的并，因此 $xz \in L \Leftrightarrow yz \in L$。

  所以 $x R_L y$。

• $(3) \rightarrow (1)$ 设 $R_L$ 具有有穷指数，下证存在 DFA $M$ 使得 $L(M) = L$。

  令 $M = (\Sigma^* / R_L, \Sigma, \delta, [\varepsilon], \{[x] | x \in L\})$，其中 $[x]$ 表示 $x$ 所在的等价类。

  其中对于任意的 $([x], a) \in (\Sigma^* / R_L) \times \Sigma$，有

  $$\delta([x], a) = [xa]$$

  下面证明 $\delta$ 的相容性（是一个函数），即 $\forall [x], [y] \in (\Sigma*/R_L). [x] = [y] \rightarrow (\forall a \in \Sigma. \delta([x], a) = \delta([y], a))$。

  由于 $[x] = [y]$，则 $x R_L y$，又由于 $R_L$ 具有右不变形，所以 $\forall a \in \Sigma. [xa] = [ya]$，成立。因此 $M$ 是一个合法的 DFA。

  根据 $R_L$ 的定义，$\forall x \in L. \delta(q_0, x) \in \{[x] | x \in L\}$。

设 $L$ 是 RL，其最小 DFA $M = (Q, \Sigma, \delta, q_0, F)$ 满足 $L(M) = L$，显然 $M$ 中不含不可达状态。根据前面的证明，有

$$|\Sigma^* / R_M| \ge |\Sigma^* / R_L|$$

下证 $M$ 与 Myhill-Nerode 定理证明中的 $M’ = (\Sigma^* / R_L, \Sigma, \delta’, [\varepsilon], \{[x] | x \in L\})$ 同构，其中

$$\delta’([x], a) = [xa]$$

定义映射 $f : Q \rightarrow \Sigma^* / R_L$，那么 $\forall q \in Q. \exists x \in \Sigma^*. \delta(q_0, x) = q_x$。令

$$f(q_x) = f(\delta(q_0, x)) = f(\delta’([\epsilon], x)) = [x]$$

这样就建立起来从 $M$ 到 $M’$ 的映射。现在证明 $f$ 是同构映射。

• 首先证明这是合法的函数，即 $q_x = q_y \Rightarrow \delta’([\varepsilon], x) = \delta’([\varepsilon], y)$
  • $q_x = q_y \Leftrightarrow \delta(q_0, x) = \delta(q_0, y) \Leftrightarrow x R_M y \Rightarrow x R_L y \Leftrightarrow [{x}] = [y] \Leftrightarrow \delta’([\varepsilon], x) = \delta’([\varepsilon], y)$
• 证明单射，即 $q_x \ne q_y \Rightarrow \delta’([\varepsilon], x) \ne \delta’([\varepsilon], y)$
  • $q_x \ne q_y \Leftrightarrow \delta(q_0, x) \ne \delta(q_0, y)$，即 $x$ 和 $y$ 在 $\Sigma^*/R_M$ 的不同等价类中
  • 如果此时 $[{x}] = [y]$，那么 $|\Sigma^* / R_M| > |\Sigma^* / R_L|$，这与 $M$ 是最小 DFA 矛盾
  • 因此 $[{x}] \ne [y]$，即 $\delta’([\varepsilon], x) \ne \delta’([\varepsilon], y)$
• 证明满射，即 $\forall [{x}]. \exists q_x \in Q. f(q_x) = [{x}]$
  • $\forall x \in L. [{x}] = \delta’([\varepsilon], x) \Leftrightarrow \exists x \in L. \delta(q_0, x) = q_x$
• 证明同态映射。在自动机中，两个状态 $q \rightarrow p$ 表示为 $\delta(q, a) = p$，因此即需要证明 $\delta(f(q), a) = f(p)$
  • 设 $\delta(q_0, x) = q$
  • $f(p) = f(\delta(q, a)) = f(\delta(\delta(q_0, x), a)) = f(\delta(q_0, xa)) = [xa]$，成立

综上，最小 DFA 都与唯一的 DFA 同构。

可以转换成正则表达式，然后直接用正则表达式表达出来。

利用乘积自动机

• 交集：构建乘积自动机，其中终止状态 $F_3 = \{[x, y] | x \in F_1 \wedge y \in F_2\}$
• 差集：构建乘积自动机，其中终止状态 $F_3 = \{[x, y] | x \in F_1 \wedge y \notin F_2\}$
• 补集：正则语言 $L$ 的补集为 $\Sigma^* - L$，由于 $\Sigma^*$ 是正则语言，因此 $L$ 的补集也是正则语言

利用正则表达式证明。设 RL $L$ 的正则表达式为 $E$，下面构建它的逆 $E^R$：

• 如果 $E$ 是字符 $a \in \Sigma$ 或 $\varepsilon$ 或 $\emptyset$，那么 $E^R = E$
• 如果 $E = F + G$，那么 $E^R = F^R + G^R$
• 如果 $E = FG$，那么 $E^R = (FG)^R = G^R F^R$
• 如果 $E = F^*$，那么 $E^R = (F^R)^*$

根据上面的规则构建的 $E^R$ 依然是正则表达式，因此 $E^R$ 仍然是 RL。

令 $L_2 = \{0^n 1^n | n \ge 0\}$，由泵引理知 $L_2$ 不是正则语言。

令 $L_3 = \{0^*1^*\}$，显然 $L_3$ 也是正则语言

假如 $L_1$ 是正则语言，那么 $L_2 = L_1 \cap L_3$ 也是正则语言，矛盾。因此原命题成立。

使用归纳法，对 $L$ 对应的正则表达式 $r$ 进行归纳易证。

由于同态映射是正则代换的特例，因此这个显然成立。

设同态映射 $f : \Sigma^* \rightarrow \Delta^*$。DFA $M(Q, \Delta, \delta, q_0, F)$，$L(M) = L$。

则 DFA $M’(Q, \Sigma, \delta’, q_0, F)$，其中

$$\delta’(q, a) = \delta(q, f(a))$$

要证明 $L(M) = L(M’)$，即证明 $\delta’(q_0, x) \in F \Leftrightarrow \delta(q_0, f(x)) \in F$。

下面先证明 $\delta(q_0, f(x)) = \delta’(q_0, x)$，对 $|x|$ 进行归纳：

• $|x| = 0$，显然成立

• 设 $|x| = |y| = k$ 的时候成立，那么当 $|x| = |ya| = k + 1$ 时，

  $$\delta(q_0, x) = \delta’(q_0, ya) = \delta’(\delta’(q_0, y), a) = \delta(\delta(q_0, f(y)), f(a)) = \delta(q_0, f(y)f(a)) = \delta(q_0, f(x))$$

由归纳知原命题成立，因此 $\delta’(q_0, x) \in F \Leftrightarrow \delta(q_0, f(x)) \in F$，即原命题成立。

设 $L_1$ 对应的 DFA 为 $M(Q, \Sigma, \delta, q_0, F)$。定义 \(M_2(Q, Σ, δ, q_0, F’)，其中

$$F’ = \{q | \exists y \in L_2, \delta(q, y) \in F\}$$

显然 $L(M’) = L_1 / L_2$