形式语言 自动机理论 理论计算机

[形式语言] 02 Finite automata

Posted by roife on Thu, Sep 23, 2021

DFA

定义

(DFA)

确定性有穷状态自动机（Deterministic finite automata，DFA）是一个五元组：

M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)

  • QQ：状态（state）的非空有穷集合
  • Σ\Sigma：输入字母表（input alphabet）
  • δ\delta：状态转移函数（transition function）
    • δ:Q×Σ→Q\delta : Q \times \Sigma \rightarrow Q
    • δ(q,a)=p\delta(q, a) = p 表示 MM 在状态 qq 下读入字符 aa，则将状态转移到 pp 并将读头指向下一字符串
  • q0q_0：开始状态（initial state），q0∈Qq_0 \in Q
  • FF：终止状态（final state）或接受状态（accept state），F⊆QF \subseteq Q

用于识别语言时可以用 δ^:Q×Σ∗→Q\hat{\delta} : Q \times \Sigma^* \rightarrow Q（为了方便起见，后面的 δ\delta 都是指 δ^\hat{\delta}）：

δ^(q,x)={q,x=εδ(δ^(q,w),a),x=wa\hat{\delta}(q, x) = \begin{cases} q, & x = \varepsilon \\ \delta(\hat{\delta}(q, w), a), & x = wa\\ \end{cases}

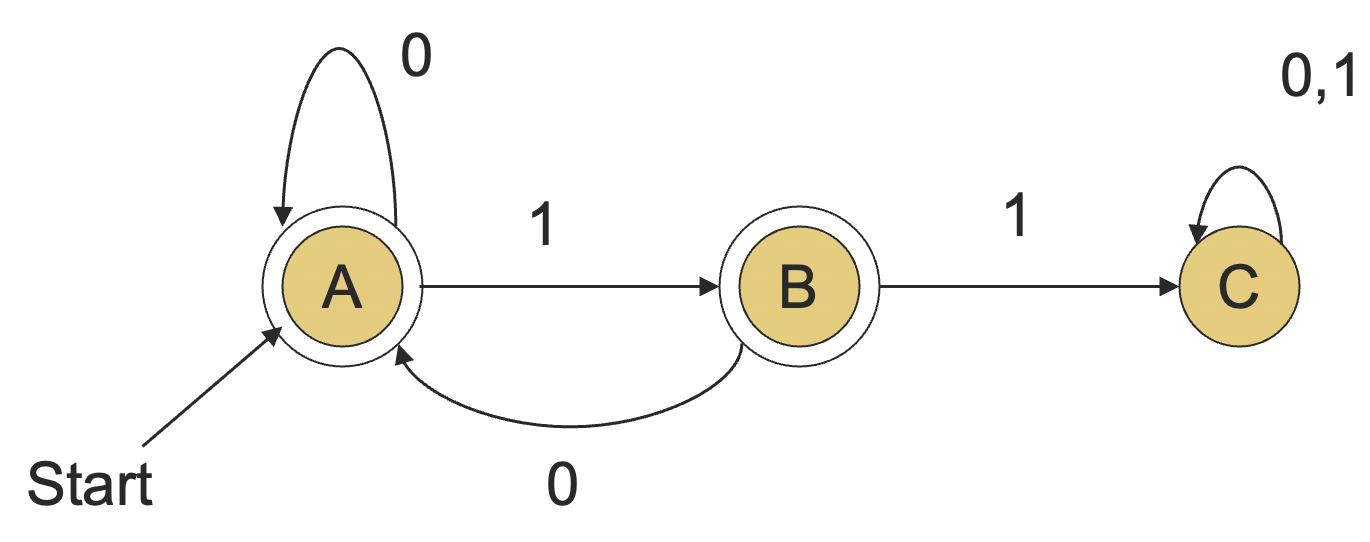
Figure 1: DFA

Figure 1: DFA

DFA 可以看成具有有穷的状态存储功能。

接受

(DFA 接受)

设 M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)，对于 ∀x∈Σ∗\forall x \in \Sigma^*，如果 δ(q0,x)∈F\delta(q_0, x) \in F，则称 xx 被 MM 接受。

L(M)={x∣δ(q0,x)∈F} L(M) = \{x | \delta(q_0, x) \in F\}

如果 L(M1)=L(M2)L(M_1) = L(M_2) 则两个 FA 等价。

即时描述

(即时描述)

设 M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)，x,y∈Σ∗x, y \in \Sigma^*，δ(q0,x)=q\delta(q_0, x) = q，则 xqyxqy 称为 MM 的一个即时描述（instantaneous description, ID），记作

xq0ay⊢Mxayqb xq_0ay \vdash_M xayqb

陷阱状态

DFA 中缺少的边（状态转移）都默认转移到一个陷阱状态（trap）中。陷阱状态只有入边，没有出边，因此 FA 会在这个陷阱状态中读完剩下的字母，并且不会接受这个字符串。

一般可以省略图中的陷阱状态。

NFA

定义

(NFA)

非确定性有穷状态自动机（non-deterministic finite automaton，NFA）

M=(Q,Σ,δ,q0,F)M =(Q, \Sigma, \delta, q_0, F)

  • Q,Σ,q0,FQ, \Sigma, q_0, F 的意义与 DFA 相同
  • δ:Q×Σ→2Q\delta: Q \times \Sigma \rightarrow 2^Q
    • δ(q,a)={p1,p2,⋯pm}∣pi⊆Q\delta(q, a) = \{p_1, p_2, \cdots p_m\} | p_i \subseteq Q 表示 MM 在状态 qq 下读入字符 aa，可以将状态转移到 pip_i 并指向下一个字符

同样 δ^\hat{\delta} 的定义也需要扩充：δ^:Q×Σ∗→2Q\hat{\delta} : Q \times \Sigma^* \rightarrow 2^Q

δ^(q,x)={{q},x=ε⋃p∈δ^(q,w)δ(p,a),x=wa\hat{\delta}(q, x) = \begin{cases} \{q\}, & x = \varepsilon \\ \bigcup_{p \in \hat{\delta}(q, w)}\delta(p, a), &x = wa \end{cases}

NFA 与 DFA 的区别在于，输入同一个字符可以有多个不同的转移路径。NFA 将 DFA 中的“值”变成了“集合”，此时可以看作是“拥有智能的”DFA，可以自动选择路径。

NFA 上的接受定义

(NFA 接受)

设 M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)，对于 ∀x∈Σ∗\forall x \in \Sigma^*，如果 δ(q0,x)∩F≠∅\delta(q_0, x) \cap F \ne \emptyset，则称 xx 被 MM 接受。

L(M)={x∣δ(q0,x)∩F≠∅} L(M) = \{x | \delta(q_0, x) \cap F \ne \emptyset\}

DFA 与 NFA 等价

注意：

  • 证明两个自动机 M,NM, N 等价，需要分别证明 (∀x∈L(M),x∈L(N))∧∀x∈L(N),x∈L(M)(\forall x \in L(M), x \in L(N)) \wedge \forall x \in L(N), x \in L(M)。
  • 证明两种自动机（两个语言类）等价，需要分别证明 (∀M∈M∗,∃N∈N∗,L(M)=L(N))∧(∀N∈N∗,∃M∈M∗,L(N)=L(M))(\forall M \in M^*, \exists N \in N^*, L(M) = L(N)) \wedge (\forall N \in N^*, \exists M \in M^*, L(N) = L(M))。

DFA 与 NFA 等价

首先，显然 DFA ⊆\subseteq NFA，下面只要证明 NFA ⊆\subseteq DFA。这个证明称为子集构造法。

给定一个 NFA M1=(Q1,Σ,δ1,q0,F1)M_1 = (Q_1, \Sigma, \delta_1, q_0, F_1)，下面要构造 DFA M2=(Q2,Σ,δ2,[q0],F2)M_2 = (Q_2, \Sigma, \delta_2, [q_0], F_2)。其中 Q2=2Q1Q_2 = 2^{Q_1}。

令 [q1,q2,…,qn][q_1, q_2, \dots, q_n] 表示一个 Q1Q_1 中的子集，对应了当前同时处于 NFA 上的 q1,q2,…,qnq_1, q_2, \dots, q_n 状态。设在 NFA 上有 δ1({q1,q2,…,qn},a)=⋃i=1nδ(qi,a)={p1,p2,…,pm}\delta_1(\{q_1, q_2, \dots, q_n\}, a) = \bigcup_{i=1}^{n}\delta(q_i, a) = \{p_1, p_2, \dots, p_m\}，则在 DFA 上对应建立转移 δ2([q1,q2,…,qn],a)=[p1,p2,…,pm]\delta_2([q_1, q_2, \dots, q_n], a) = [p_1, p_2, \dots, p_m]。

接收状态集合 F2={[P⊆2Q1]∣F∩P≠∅}F_2 = \{[P \subseteq 2^{Q_1}] | F \cap P \ne \emptyset\}。

当有些状态构造出来可能实际上无法从初始状态转移过来时，这些状态可以被删掉。

下面通过归纳 ∣w∣|w| 证明 M1=M2M_1 = M_2：

  • 基础情况：w=εw = \varepsilon，显然成立
  • 归纳：设 w=xaw = xa，则
    • δ1(q0,xa)=⋃p∈δ1(q0,x)δ1(p,a)\delta_1(q_0, xa) = \bigcup_{p \in \delta_1(q_0, x)}\delta_1(p, a)
    • δ2([q0],w)=⋃p∈δ2([q0],x)δ2(p,a)\delta_2([q_0], w) = \bigcup_{p \in \delta_2([q_0], x)}\delta_2(p, a)
    • 由归纳假设知 δ1(q0,x)=δ2([q0],x)\delta_1(q_0, x) = \delta_2([q_0], x)，且 ∀p∈V,a∈T.δ1(p,a)=δ2([p],a)\forall p \in V, a \in T. \delta_1(p, a) = \delta_2([p], a)

在这个构造中用 DFA 的一个点，表示了在 NFA 上“同时处于多个点”的状态，所以 DFA 至多有 2n2^n 个点。这个方法的巧妙之处在于尽管 NFA 是不确定性的，但是 NFA 的状态空间是有限的，因此可以用 DFA 构造出 NFA 的所有状态。

ε\varepsilon-NFA

定义

(ε\varepsilon-NFA)

带空转移的非确定性有穷状态自动机（non-deterministic finite automaton with ε\varepsilon moves，ε\varepsilon-NFA）

M=(Q,Σ,δ,q0,F)M =(Q, \Sigma, \delta, q_0, F)

  • Q,Σ,q0,FQ, \Sigma, q_0, F 的意义与 DFA 相同
  • δ:Q×(Σ∪{ε})→2Q\delta: Q \times (\Sigma \cup \{ \varepsilon \}) \rightarrow 2^Q
    • 对于 δ(q,s)={p1,p2,⋯pm}\delta(q, s) = \{p_1, p_2, \cdots p_m\} 表示 MM 在状态 qq 下读入字符 aa，则可以将状态转移到 pip_i 并将读头指向下一个字符
    • 对于 δ(q,ε)={p1,p2,⋯pm}\delta(q, \varepsilon) = \{p_1, p_2, \cdots p_m\} 表示 MM 在状态 qq 下不读入字符，并将状态转移到 pip_i

同样 δ^\hat{\delta} 的定义也需要扩充：δ^:Q×Σ∗→2Q,P⊆Q,q∈Q,w∈Σ∗,a∈Σ\hat{\delta} : Q \times \Sigma^* \rightarrow 2^Q, P \subseteq Q, q \in Q, w \in \Sigma^*, a \in \Sigma

(闭包)

状态集合 PP 的闭包定义如下：

ε−CL(P)={{q∣p→εq∈δ},P={p}⋃p∈Pε−CL(p),else\varepsilon-CL(P)= \begin{cases} \{q \vert p \overset{\varepsilon}{\rightarrow} q \in \delta \}, &P = \{p\} \\ \bigcup_{p \in P} \varepsilon-CL(p), &\text{else} \end{cases}

当然 δ(q,ε)=q\delta(q, \varepsilon) = q

则

δ^(q,x)={ε−CL(q),x=ε⋃p∈δ^(q,w)ε−CL(δ(p,a)),x=wa\hat{\delta}(q, x) = \begin{cases} \varepsilon-CL(q), & x = \varepsilon \\ \bigcup_{p \in \hat{\delta}(q, w)}\varepsilon-CL(\delta(p, a)), &x = wa \end{cases}

注意在这里 δ(q,ε)≠δ^(q,ε)\delta(q, \varepsilon) \ne \hat{\delta}(q, \varepsilon)。

ε\varepsilon-NFA 上的接受定义

(ε\varepsilon-NFA 的接受)

设 M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)，对于 ∀x∈Σ∗\forall x \in \Sigma^*，如果 δ^(q0,x)∩F≠∅\hat{\delta}(q_0, x) \cap F \ne \emptyset，则称 xx 被 MM 接受。

L(M)={x∣δ^(q0,x)∩F≠∅} L(M) = \{x | \hat{\delta}(q_0, x) \cap F \ne \emptyset\}

NFA 与 ε\varepsilon-NFA 等价

NFA 与 ε\varepsilon-NFA 等价。

给定一个 ε\varepsilon-NFA M1=(Q,Σ,δ1,q0,F1)M_1 = (Q, \Sigma, \delta_1, q_0, F_1)，下面要构造 NFA M2=(Q,Σ,δ2,q0,F2)M_2 = (Q, \Sigma, \delta_2, q_0, F_2)。

其中

δ2(q,a)=δ^1(q,a) \delta_2(q, a) = \hat{\delta}_1(q, a)

F2={q∣ε−CL(q)∩F1≠∅}F_2 = \{q | \varepsilon-CL(q) \cap F_1 \ne \emptyset\}

等价性可以通过归纳证明。

由上可知 DFA，NFA，ε\varepsilon-NFA 三者两两等价。

正则语言与 FA

RL 与 FA 等价

RL 与 FA 等价。

只要证明 RL ⊆\subseteq FA，且 FA ⊆\subseteq RL 即可。

  • 首先证明 FA 能够接受 RL。需要对于任意 RL，要构造一个与之等价的 FA。对于正则文法 G=(V,T,P,S)G = (V, T, P, S)，构造 M=(V∪{Z},T,δ,S,{Z})M = (V \cup \{Z\}, T, \delta, S, \{Z\})，其中 δ\delta 的定义如下：

    δ(A,a)={{B∣A→aB∈P}∪{Z},A→a∈P{B∣A→aB∈P},A→a∉P\delta(A, a) = \begin{cases} \{B | A \rightarrow aB \in P\} \cup \{Z\}, & A \rightarrow a \in P \\ \{B | A \rightarrow aB \in P\} , & A \rightarrow a \notin P \end{cases}

    下面证明 L(M)=L(G)L(M) = L(G)。设 a1a2…an∈L(G)a_1 a_2 \dots a_n \in L(G)，即有推导

    S⇒+a1a2…an⇔S⇒a1A1⇒a1a2A2⇒⋯⇒a1a2…an\begin{aligned} & S \xRightarrow{+} a_1 a_2 \dots a_n \\ \Leftrightarrow& S \Rightarrow a_1 A_1 \Rightarrow a_1 a_2 A_2 \Rightarrow \dots \Rightarrow a_1 a_2 \dots a_n \end{aligned}

    因此

    S→a1A1∈PA1→a2A2∈P…An−2→an−1An−1∈PAn−1→an∈P\begin{aligned} & S \rightarrow a_1 A_1 \in P \\ & A_1 \rightarrow a_2 A_2 \in P \\ & \dots \\ & A_{n-2} \rightarrow a_{n-1} A_{n-1} \in P \\ & A_{n-1} \rightarrow a_n \in P \end{aligned}

    根据此文法，对于 δ\delta 有

    A1∈δ(S,a1)A2∈δ(A1,a2)…An−1∈δ(An−2,an−1)Z∈δ(An−1,an)\begin{aligned} & A_1 \in \delta(S, a_1) \\ & A_2 \in \delta(A_1, a_2) \\ & \dots \\ & A_{n-1} \in \delta(A_{n-2}, a_{n-1}) \\ & Z \in \delta(A_{n-1}, a_n) \end{aligned}

    因此 Z∈δ(S,a1a2…an)Z \in \delta(S, a_1 a_2 \dots a_n)，成立。

    这里需要特殊处理 ε\varepsilon 的情况。不妨假设 SS 不出现在任何产生式的右部。设 S→ε∈PS \rightarrow \varepsilon \in P，则定义转移 δ(S,ε)={Z}\delta(S, \varepsilon) = \{Z\}，由于 SS 不出现在产生式的右部，因此 FA 上的转移无法回到 SS，即这个转移不会对其他句子的接受产生影响。

  • 下面证明 FA 接受的句子都是 RL。由于三种 FA 等价，因此这里只需要证明 DFA 接受的句子是 RL。设 DFA M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)，构造 G=(Q,Σ,P,q0)G = (Q, \Sigma, P, q_0)，其中

    P={q→ap∣δ(q,a)=p}∪{q→a∣δ(q,a)=p∈F}P = \{ q \rightarrow a p | \delta(q, a) = p \} \cup \{q \rightarrow a | \delta(q, a) = p \in F \}

    证明类似。同样这里需要考虑 ε\varepsilon 相关的句子。假设 q0∉Fq_0 \notin F，则 ε∉L(M)\varepsilon \notin L(M)，不影响。如果 q0∈Fq_0 \in F，由于空句子存在与否不影响语言性质，因此存在正则文法 G’G’ 使得 L(G’)=L(G)∪{ε}=L(M)L(G’) = L(G) \cup \{\varepsilon\} = L(M)。

综上，命题成立。

左线性文法与 FA 等价

类似 RL 与 FA 等价的证明。只不过 RL 中证明利用了“推导”的顺序，而左线性文法的证明利用了“规约”的顺序。

左线性文法的语言与 FA 等价。

  • 首先证明 FA 能够接受左线性文法的语言。对于左线性文法 G=(V,T,P,Z)G = (V, T, P, Z)，构造 M=(V∪{S},T,δ,S,{Z})M = (V \cup \{S\}, T, \delta, S, \{Z\})，其中 δ\delta 的定义如下：

    δ(B,a)={{A∣A→a∈P},B=S{A∣A→Ba∈P},B≠S\delta(B, a) = \begin{cases} \{A | A \rightarrow a \in P\} , & B = S \\ \{A | A \rightarrow Ba \in P\} , & B \ne S \end{cases}

    利用规约可以证明。

  • 然后证明 FA 接受的语言可以用左线性文法描述。对于 DFA M=(Q,Σ,δ,q0,F)M = (Q, \Sigma, \delta, q_0, F)，构造 G=(Q,Σ,P,qz)G = (Q, \Sigma, P, q_z)，其中

    P={p→qa∣δ(q,a)=p}∪{p→a∣δ(q0,a)=p}∪{qz→qa∣δ(q,a)=p∈F}P = \{ p \rightarrow q a | \delta(q, a) = p \} \cup \{p \rightarrow a | \delta(q_0, a) = p \} \cup \{q_z \rightarrow q a | \delta(q, a) = p \in F \}

左右线性文法等价

左右线性文法等价

由于二者皆与 FA 等价，因此二者等价。

FA 的变形

双向 FA

(2DFA)

确定性双向有穷状态自动机（two-way deterministic finite automation, 2DFA）是一个八元组

M=(Q,Σ,⊢,⊣,δ,q0,t,r)M = (Q, \Sigma, \vdash, \dashv, \delta, q_0, t, r)

  • 其中 Q,Σ,q0,FQ, \Sigma, q_0, F 的意义同 DFA。
  • ⊢,⊣\vdash, \dashv 分别是起始符号和末尾符号，且 ⊢∉Σ∧⊣∉Σ\vdash \notin \Sigma \wedge \dashv \notin \Sigma
  • t,rt, r 分别是接受状态和拒绝状态，且 t≠rt \ne r
  • δ:(Q∖{t,r})×(Σ∪{⊢,⊣})→Q×{L,R}\delta : (Q \setminus \{t, r\}) \times (\Sigma \cup \{\vdash, \dashv\}) \rightarrow Q \times \{L, R\}
    • 如果 δ(q,a)={p,L}\delta(q, a) = \{p, L\} 则表示状态转移后讲读头向左移动一个方格，指向前一个字符
    • 如果 δ(q,a)={p,R}\delta(q, a) = \{p, R\} 则表示状态转移后读头向右移动移位，指向下一个字符
    • ∀q∈Q∖{t,r}.δ(q,⊢)=(p,R) (p∈Q)\forall q \in Q \setminus \{t, r\}. \delta(q, \vdash) = (p, R)\ (p \in Q)
    • ∀q∈Q∖{t,r}.δ(q,⊣)=(p,L) (p∈Q)\forall q \in Q \setminus \{t, r\}. \delta(q, \dashv) = (p, L)\ (p \in Q)

设 2DFA M=(Q,Σ,⊢,⊣,δ,q0,t,r)M = (Q, \Sigma, \vdash, \dashv, \delta, q_0, t, r)，其接受的语言为

L(M)={x∣q0x⊢∗xt}L(M) = \{x | q_0 x \vdash^{*} xt\}

有趣的是，2DFA 也被称为只读图灵机（read-only Turing Machine），因为它长度有限且无法在纸带上打印东西。

2DFA 与 FA 等价。

显然 DFA ∈\in 2DFA，因此只要证明 2DFA∈DFA2DFA \in DFA.

设 2DFA M=(Q1,Σ,⊢,⊣,s,δ1,t,r)M = (Q_1, \Sigma, \vdash, \dashv, s, \delta_1, t, r)，下面构造 NFA M’=(Q2,Σ,δ2,q0,F)M’ = (Q_2, \Sigma, \delta_2, q_0, F)。

注意到 2DFA 的状态仅与读头位置和当前状态相关。

假设目前状态为 qq，将需要读入的串 x=yzx = yz 分为两段，2DFA 的读头可以若干次穿越两段的分割点。将其穿越分割点后的状态记录下来，称其为有效穿越序列（valid crossing sequence）。

设有效穿越序列 C=q1q2…qnC = q_1 q_2 \dots q_n 如果 2DFA 接受这个串，那么：

  • 有效穿越序列的长度满足 ∣C∣≡1(mod  2)|C| \equiv 1 (\mod 2)
  • 有效穿越序列的第一个状态一定是向右的，并且后面顺序一定是左右交替，并且最后一次穿越是向右的
  • ∀qi,qj∈C.qi=qj→∣j−i∣≡1(mod  2)\forall q_i, q_j \in C. q_i = q_j \rightarrow |j-i| \equiv 1 (\mod 2)，即同样的状态在 CC 中的位置不可能同奇同偶
    • “同奇同偶”说明读头两次在同一位置出现了重复的状态，说明状态机陷入了循环，这个字符串无法到达终止状态
    • 由鸽巢定理，容易知道 ∣C∣<2∣Q1∣|C| < 2|Q_1|，即同一位置的有效穿越序列有限，数量不超过 ∣Q∣2∣Q∣|Q|^{2|Q|}

由上面的性质，考虑将当前读头所在位置所对应的有效穿越序列编码为 NFA 的状态。NFA 在某个位置的状态，对应 2DFA 读入这个串后在这个位置留下的有效穿越序列。NFA 的读头只能从左向右移动，每次读入一个字符，然后 NFA 状态会转移到下一个位置的有效穿越序列。当然，由于 2DFA 可能采取不同的路径来回穿越下一个位置，因此下一个位置的有效穿越序列有很多种可能，所以这里需要使用 NFA。

为了能够定义有效穿越序列的匹配，下面首先需要定义左匹配与右匹配。自动机在一个位置上向右运动穿越字符时，前后位置对应的有效穿越序列称为右匹配；反之，称为左匹配。当 2DFA 接受字符串后，每个位置的有效穿越序列的最后一次移动都是向右的，因此此时每个位置和它右侧相邻位置的有效穿越序列构成右匹配。所以 NFA 的状态转移之间需要存在右匹配关系。

设存在两个有效穿越序列 C1=[pi],C2=[qj]C_1 = [p_i], C_2 = [q_j]，下面针对读头在两个位置和其移动方向进行讨论：

  • C1=ε,C2=εC_1 = \varepsilon, C_2 = \varepsilon 互为左右匹配
  • 如果 C1C_1 是 C2C_2 的左匹配，即读头在 C1C_1 上，且 δ1(pl,a)=(qk,R)\delta_1(p_l, a) = (q_k, R)，那么 C2qkC_2 q_k 是 C1plC_1 p_l 的右匹配
  • 如果 C2C_2 是 C1C_1 的右匹配，即读头在 C2C_2 上，且 δ1(qk,a)=(pl,R)\delta_1(q_k, a) = (p_l, R)，那么 C1plC_1 p_l 是 C2qkC_2 q_k 的左匹配
  • 如果 C1C_1 是 C2C_2 的左匹配，即读头在 C1C_1 上，且 δ1(pl,a)=(p’,L)\delta_1(p_l, a) = (p’, L)，那么 C1plC_1 p_l 是 C2C_2 的左匹配
  • 如果 C2C_2 是 C1C_1 的右匹配，即读头在 C2C_2 上，且 δ1(qk,a)=(q’,R)\delta_1(q_k, a) = (q’, R)，那么 C2qkC_2 q_k 是 C1C_1 的右匹配

下面是更加严格的定义：

  • Q2={C=[q1q2…qn]∣C is a valid crossing sequence for M}Q_2 = \{C = [q_1 q_2 \dots q_n] | \text{$C$ is a valid crossing sequence for $M$}\}
  • δ2([pi],a)={[qj]∣[qj] right matches p[l]}\delta_2([p_i], a) = \{[q_j] | \text{$[q_j]$ right matches $p[l]$} \}
  • q0=[s]q_0 = [s]
  • F={[pit]}F = \{[p_i t]\}

下面简单证明一下 L(M)=L(M’)L(M) = L(M’)。根据上面的构造显然有 L(M)⊆L(M’)L(M) \subseteq L(M’)；而在 M2M_2 中，假设存在 δ2([pi],a)=[qj]\delta_2([p_i], a) = [q_j]，即 [qj][q_j] 是 [pi][p_i] 右匹配，根据上面对于有效穿越序列匹配的讨论实际上就构建了可以被 MM 所接受的字符串，因此 L(M’)⊆L(M)L(M’) \subseteq L(M)。

构造完成后，又由于 DFA=NFADFA = NFA，因此有 2DFA∈DFA2DFA \in DFA。

类似可以定义 2NFA。

带输出的 FA

带输出的 FA 分为两类：Moore 机和 Mealy 机。

(Moore 机)

Moore 机是一个六元组 M=(Q,Σ,Δ,δ,λ,q)M = (Q, \Sigma, \Delta, \delta, \lambda, q)：

  • Q,Σ,q0,δQ, \Sigma, q_0, \delta 的意义同 FA
  • Δ\Delta 是输出字母表
  • λ\lambda 是输出函数，λ:Q→Δ\lambda : Q \rightarrow \Delta，其中 λ(q)=a\lambda (q) = a 表示在状态 qq 下会输出 aa

(Mealy 机)

Mealy 机是一个六元组 M=(Q,Σ,Δ,δ,λ,q)M = (Q, \Sigma, \Delta, \delta, \lambda, q)：

  • Q,Σ,q0,δQ, \Sigma, q_0, \delta 的意义同 FA
  • Δ\Delta 是输出字母表
  • λ\lambda 是输出函数，λ:Q×Σ→Δ\lambda : Q \times \Sigma \rightarrow \Delta，其中 λ(q,a)=d\lambda (q, a) = d 表示在状态 qq 下读入 aa 会输出 dd

读入相同的串，moore 机和 mealy 机表现不同：

  • Moore 机输出 λ(q0)λ(q1)…λ(qn)\lambda(q_0) \lambda(q_1) \dots \lambda(q_n)，长度为 n+1n + 1
  • Mealy 机输出 λ(q0,a1)λ(q1,a2)…λ(qn,an−1)\lambda(q_0, a_1) \lambda(q_1, a_2) \dots \lambda(q_n, a_{n-1})，长度为 nn

(Moore 机和 Mealy 机的等价性)

对于 moore 机 M1(Q1,Σ,Δ,δ1,λ1,q01)M_1(Q_1, \Sigma, \Delta, \delta_1, \lambda_1, q_{01}) 和 mealy 机 M2(Q2,Σ,Δ,δ2,λ2,q02)M_2(Q_2, \Sigma, \Delta, \delta_2, \lambda_2, q_{02})，如果 ∀x∈Σ∗,T1(x)=λ1(q0)T2(x)\forall x \in \Sigma^*, T_1(x) = \lambda_1(q_0) T_2(x)，则称二者等价。

事实上，moore 机的描述能力和 mealy 机是等价的，因此对于任意的机器，可以构造与之等价的另一种机器。

Moore 机与 Mealy 机描述能力等价。

下面给出二者互相转换的思路。

  • Moore to Mealy：只要将状态前移半个周期即可。设 Moore 机 M1=(Q,Σ,Δ,δ,λ1,q)M_1 = (Q, \Sigma, \Delta, \delta, \lambda_1, q)，令 Mealy 机 M2=(Q,Σ,Δ,δ,λ2,q)M_2 = (Q, \Sigma, \Delta, \delta, \lambda_2, q)，其中

    ∀x:Σ,δ(p,x)=q∧λ1(q)=a→λ(p,x)=a\forall x : \Sigma, \delta(p, x) = q \wedge \lambda_1(q) = a \rightarrow \lambda(p, x) = a

  • Mealy to Moore：考虑将每种转移来的路径对应到一个状态，用 [p,q,x][p, q, x] 表示从 pp 转移到 qq，造成转移读取的字符为 xx。令 Mealy 机为 M1=(Q1,Σ,Δ,δ1,λ1,q)M_1 = (Q_1, \Sigma, \Delta, \delta_1, \lambda_1, q)，Moore 机为 M2=(Q2,Σ,Δ,δ2,λ2,q)M_2 = (Q_2, \Sigma, \Delta, \delta_2, \lambda_2, q)，则

    • Q2={[p,q,x]∣δ1(p,q)=x,p∈Q1,q∈Q1}Q_2 = \{ [p, q, x] | \delta_1(p, q) = x, p \in Q_1, q \in Q_1 \}
    • ∀p:δ(p,x)=q.∀r:δ(q,y)=r.δ([p,q,x],y)=[q,r,y]\forall p : \delta(p, x) = q. \forall r : \delta(q, y) = r. \delta([p, q, x], y) = [q, r, y]
    • ∀[p,q,x]∈Q2,λ2([p,q,x])=λ1(p,x)\forall [p, q, x] \in Q_2, \lambda_2([p, q, x]) = \lambda_1(p, x)

一个有趣的题

定义语言 LL 上的运算 Hlf⁡\operatorname{\mathrm{Hlf}} 为 Hlf⁡(L)={x∣∃y.∣x∣=∣y∣∧xy∈L}\operatorname{\mathrm{Hlf}}(L) = \{x | \exists y. |x| = |y| \wedge xy \in L\}。

证明 RL 对于 Hlf⁡\operatorname{\mathrm{Hlf}} 封闭。

不妨设 RL LL 对应 DFA M(Q,Σ,δ,q0,F)M(Q, \Sigma, \delta, q_0, F)，现构造一个 FA M’(Q∪{q0’},Σ,δ’,q0’,∅)M’(Q \cup \{q_0’\}, \Sigma, \delta’, q_0’, \emptyset)，其中

δ’(q,ε)={F,q=q0’{p∣∃b∈Σ.δ(p,b)=q},q∈Q\delta’(q, \varepsilon) = \begin{cases} F, & q = q_0’ \\ \{ p | \exists b \in \Sigma. \delta(p, b) = q \}, & q \in Q \end{cases}

即 M’M’ 是一个从 MM 的终态集开始与 MM 逆向运动的状态机。下面用这两个状态机来联合构造一个 FA M’’(Q×2Q,Σ,δ’’,[q0,F],F’’)M’’(Q \times 2^Q, \Sigma, \delta’’, [q_0, F], F’’)，其中

  • F’’={[q,q]∣q∈Q}F’’ = \{[q, q] | q \in Q\}
  • δ’’([q,p],a)={[s,t]∣δ(q,a)=s∧t∈δ’(p,a)}\delta’’([q, p], a) = \{[s, t] | \delta(q, a) = s \wedge t \in \delta’(p, a)\}

M’’M’’ 的状态有两个分量，第一个分量表示 MM 的运动，即对于 xx 的构造；第二个分量表示 M’’M’’ 的运动，即对于 yy 的构造。由于每次转移两个分量都需要走一步，因此 ∣x∣=∣y∣|x| = |y|。当两个分量的状态相遇时，满足 xy∈Lxy \in L。

CATALOG