Introduction
介绍
PRE 之类的优化一般会在优化的同时移动代码以保证代码的合法性,这使得优化算法变得十分复杂。这篇论文提出应当用一个独立的 pass 来移动代码,来让优化算法变得更简单。
为此这篇论文提出了 global code motion (GCM) 算法,其复杂度接近于线性,能够将代码尽量移动到循环外或分支内,从而降低运行时的开销。此外,这篇论文还提出了 global value numbering (GVN) 的一种实现。对于计算结果相同的多个指令,GVN 会把重复计算的指令替换成第一个指令的拷贝。由于 GVN 算法基于遍历和 hash-table,在替换时可能会破坏指令的支配性,因此需要 GCM 来修复支配问题。
程序表示
以下假设程序都以 CFG 和 SSA 的形式呈现,能够使用 def-use 链进行指令的替换。指令内的变量通过指针的方式指向其定义,而不用变量名表示(类似 LLVM 内部 LLVM IR 的结果)。
除了基于 CFG 外,程序之间还有基于数据依赖的 program dependence graph (PDG):
- 如果一个指令是另一个指令的操作数,那么后者依赖于前者;
- phi 指令、分支指令、返回指令依赖所在的基本块;
- 内存存取指令依赖 memory token 或有其他的依赖边(load 依赖 store,这样防止读写顺序出现问题);
- 陷入指令(faulting)依赖所在的基本块。
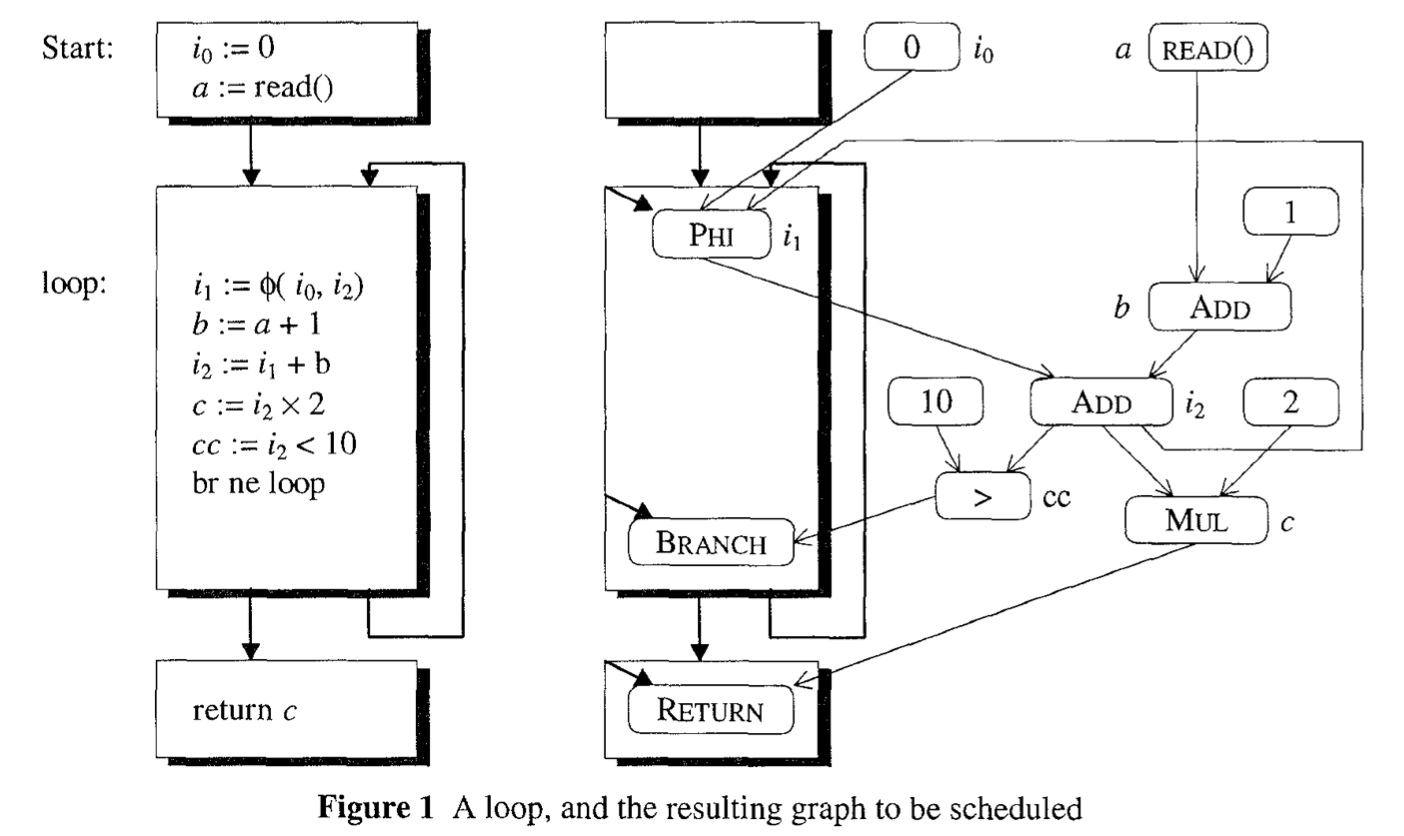
Figure 1: Dependence graph
对基本块有依赖的指令都被 pin 在基本块上;所有的寄存器指令都没有对基本块的依赖,因此寄存器指令是“浮动”的,可以放置在任何基本块中(只要保证依赖顺序和控制流即可)。GCM 的任务就是将这些“浮动”的指令放在合适的基本块中:尽量放在循环外、分支内。
Global code motion
SSA 中的支配性
为了方便表述,这里就用“指令”代指“指令所在的基本块”。
要理解 GCM 算法,最关键的一点在于理解“一个指令可以放在哪里?”。在 SSA 中要求为:
- 指令的所有操作数都能支配这个指令(除了 phi 指令,因为 phi 指令本来就是在支配边界上的汇总)
- 因此在支配树中,指令的所有操作数的定义都在它到根结点的路径上
- 指令只能顺着它到根结点的路径进行移动,否则将破坏支配关系
- 这个指令能够支配其所有 users(包括 phi 指令)
- 因此所有的 users 必须在指令的子树中
- 指令在移动后必须还是其 users 的根
在原始程序中,这两条性质可能不成立。例如下面这个程序:
/* bb_first */
int x = 0;
if (/* bb_cond */) {
/* bb_then */
x = 1;
}
/* bb_use */
在这个程序中,支配树为:

Figure 2: Misunderstanding of properties 1 for dom-tree in SSA
看起来似乎不太对,因为 bb_use 依赖于 bb_then,但是在支配树上却没有依赖它。但是转换为 SSA 后,这个程序变成了这样:
/* bb_first */
int x1 = 0;
if (/* bb_cond */) {
/* bb_then */
x2 = 1;
}
/* bb_use */
x_phi = phi(x1, x2);
// use x_phi
此时新增了一个 x_phi 来汇总两条分支的结果,这样在 bb_use 中使用 x 时,其使用的实际上是 x_phi,满足了第一条要求。因此在 SSA 中,这些 phi 指令非常重要,不能轻易删除。
算法步骤
基于此,GCM 算法的大体步骤如下:
- 构建支配树,并且标记每个基本块在支配树中的深度
- 构建循环树,并且计算每个基本块所在的循环深度
- 执行 schedule early 算法,将指令尽可能地前移
- 为了保证合法,只能移动到被指令的所有操作数所支配的最浅基本块
- 由于指令只能沿着它到根结点的路径移动,因此最浅基本块即在支配树上深度最浅的结点
- 此时指令和其 user 隔得很远,这个寄存器的声明周期很长
- 执行 schedule late 算法,将所有的指令尽可能后移
- 为了保证合法,只能移动到能够支配所有 user 的最深基本块
- 同理,最深基本块为支配树上深度最深的结点
- 此时 early 和 late 之间的所有位置都是合法位置,可以任意挑一个放
- 为了达成最优效果,使用前两步的信息进行选择:循环深度最浅且尽量在分支内的基本块
计算支配树和循环树
对于这两步已经有很多成熟的算法。其中,在实际使用中得到循环信息的最简单的方法是在从 AST 构建 SSA 时就记下这个基本块所在的循环深度。
Schedule Early
Schedule early 算法需要将指令移动到被所有操作数所支配的最浅基本块。由于一部分指令是被 pin 在基本块上不可移动的,因此不妨以它们为源点从后往前进行移动。对于一个指令,先将其操作数尽可能前移,然后再移动指令本身,这样能达到更好的效果。
\begin{algorithm} \caption{Schedule Early} \begin{algorithmic} \procedure{main}{$insts$} \state set all instructions in $insts$ to be unvisited \for {$inst \in insts$} \if {$inst$ is pinned} \state set $inst$ to be visited \for {$op \in$ operands of $inst$} \state \call{ScheduleEarly}{$op$} \endfor \endif \endfor \state \comment{Run ScheduleLate later} \endprocedure \state \procedure{ScheduleEarly}{$inst$} \if {$inst$ is visited} \return \endif \state set $inst$ to be visited \state $earlyBB_{inst} \gets root$ \for {$op \in$ operands of $inst$} \state \call{ScheduleEarly}{$op$} \state $opBB \gets$ bb of $op$ \if {depth of $opBB$ $<$ depth of $earlyBB_{inst}$} \state $earlyBB_{inst} \gets $ bb of op \endif \endfor \endprocedure \end{algorithmic} \end{algorithm}
上面的例子经过 schedule early 移动后变成下图。
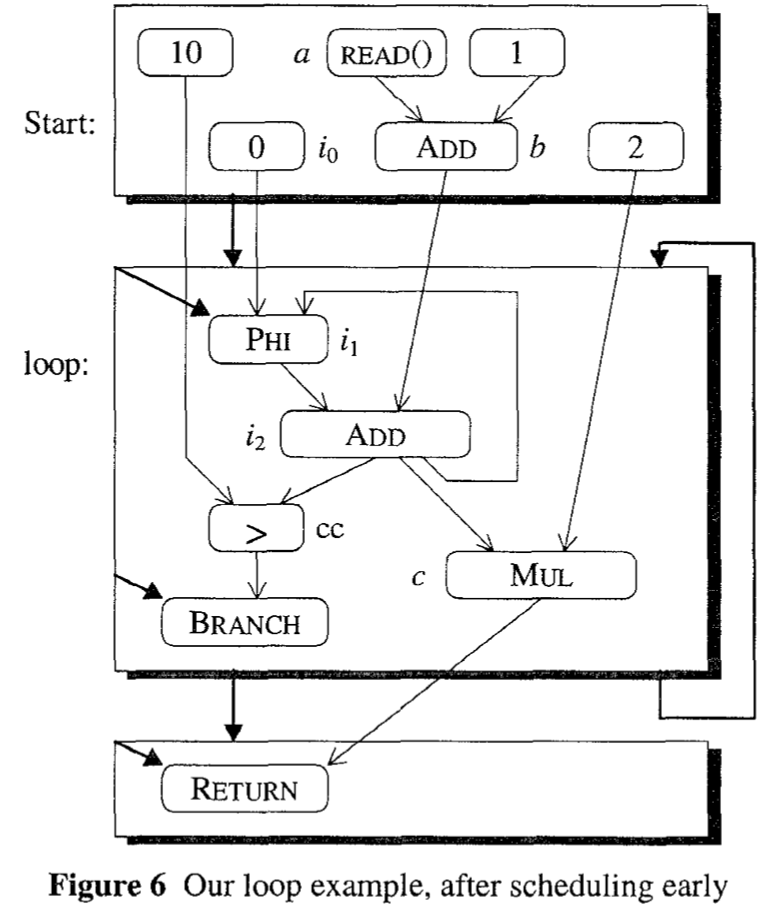
Figure 3: After Schedule Early
Schedule late
Schedule late 算法会将一个指令移动到能够支配其所有 users 的最深基本块。同理,可以从 pin 住的指令为源点遍历。对于一个指令,为了能让它尽可能后移,需要先把它的所有 users 后移,再移动这个指令本身。此时要让这个指令仍然支配其所有的 users,那么就是要将这个指令移动到所有 users 的 LCA 上。
这里需要注意的一点是,phi 指令如果用了一个操作数,那么它对这个操作数的 use 是计算在它的对应前驱基本块上的。这是因为在消除 phi 指令时,会在其前驱基本块内插入 copy 赋值语句。
由于一个指令的 users 的位置会影响到这个指令最深能放置的基本块,因此在 schedule late 中就需要彻底确定 users 的放置位置。
\begin{algorithm} \caption{Schedule Late} \begin{algorithmic} \procedure{main}{$insts$} \state \comment{Run ScheduleEarly in advance} \state set all instructions in $insts$ to be unvisited \for {$inst \in insts$} \if {$inst$ is pinned} \state set $inst$ to be visited \for {$user \in$ users of $inst$} \state \call{ScheduleLate}{user} \endfor \endif \endfor \endprocedure \state \procedure{ScheduleLate}{$inst$} \if {$inst$ is visited} \return \endif \state set $inst$ to be visited \state $lca \gets \top$ \for {$user \in$ users of $inst$} \state \call{ScheduleLate}{$user$} \state $bb \gets$ bb of $user$ \if {$user$ is a $\phi$ node} \state $bb \gets$ corresp. bb for $inst$ in $\phi$ \endif \state $lca \gets $ \call{FindLca}{$lca, bb$} \endfor \state \comment{Place $inst$} \state \comment{Remember $earlyBB_i$ has been worked out in ScheduleEarly} \state $bestBB \gets lca$ \state $curBB \gets lca$ \while {depth of $curBB$ $>=$ depth of $earlyBB_{inst}$} \if {loop nested level of $curBB$ $<$ loop nested leval of $bestBB$} \state $bestBB \gets curBB$ \endif \state $curBB \gets$ immediate dominator of $curBB$ \endwhile \state move $inst$ into $bestBB$ \endprocedure \state \procedure{FindLca}{$a, b$} \state \comment{Here use the simple linear algorotihm to find LCA} \state \comment{It will be faster to use ST-RMQ algorithm} \if {$a$ is $\top$} \return{$b$} \endif \while{depth of $a$ $<$ depth of $b$} \state $a \gets$ immediate dominator of $a$ \endwhile \while{depth of $a$ $>$ depth of $b$} \state $b \gets$ immediate dominator of $b$ \endwhile \while{$a \ne b$} \state $a \gets$ immediate dominator of $a$ \state $b \gets$ immediate dominator of $b$ \endwhile \endprocedure \end{algorithmic} \end{algorithm}
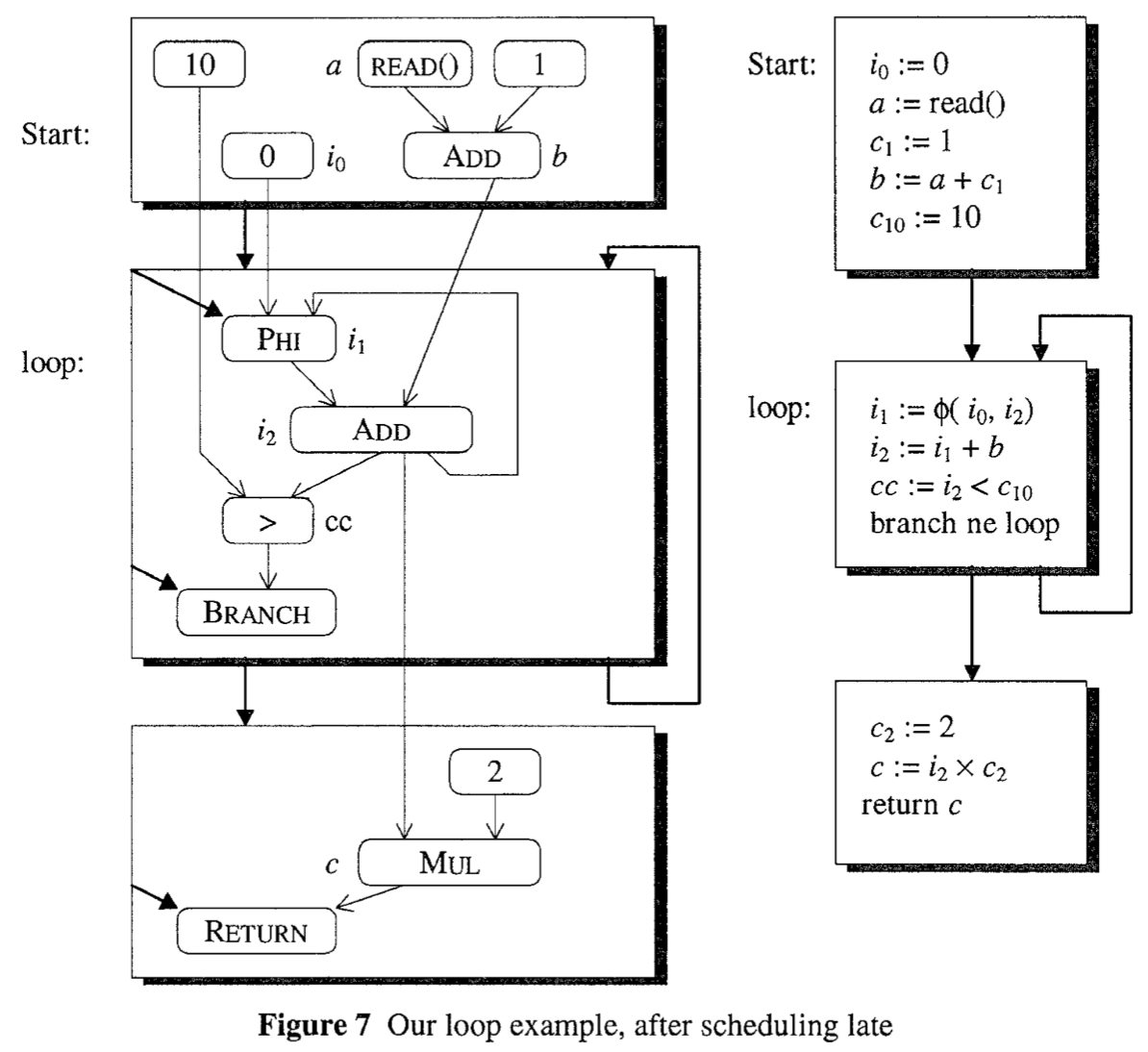
Figure 4: After Schedule Late
Global value numbering
有了 GCM 后,GVN 的实现就非常简单了。对图使用逆后序遍历(保证先访问一个结点所有的前驱,再访问这个结点),途中对每条指令进行下面的优化:
- 尝试对这条指令进行常量折叠等代数化简
- 如果能化简,就用
replaceAllUseWith将这个指令置换成化简后的表达式
- 如果能化简,就用
- 如果无法化简,以操作数和操作符为 key,尝试在哈希表中查找有没有对应的项
- 如果找到了,就用
replaceAllUseWith将其替换成哈希表中 key 对应的 value
- 如果找到了,就用
- 如果没找到,以操作数和操作符为 key,这条指令为 value,将其登记到哈希表中
在这个过程中直接进行遍历,不考虑基本块的先后顺序,因此会导致两个问题:
- 一条指令被替换成其另一条指令,但是那条指令并不支配这条指令的 users
- 这个问题可以通过 GCM 解决。在 GCM 中只考虑 value dependency,不考虑基本块,所以最终会根据 dependency 将那条指令移动到正确的位置
- 不同的遍历顺序可能导致化简的结果不同
- 可以跑多次 GVN 直到一个不动点,一般来说跑两次就足够了
在实际算法中,可以根据不同的指令用不同的哈希算法。例如对于可交换的运算使用满足交换律的哈希函数。