相关工作
Cytron1991
- 优势
- 生成 minimal SSA
- 劣势
- 输入程序必须是 CFG 形式
- 需要进行其他的分析,例如支配信息等
工业界的编译器
- LLVM:Cytron1991
- Java Hotpot VIM:用生成非 minimal/pruned SSA 的算法
Brain2013
- 优势
- 生成 minimal and pruned SSA
- 可以直接从 ASST 或 bytecode 翻译
- 不需要额外的前置分析
- 可以在构建时使用优化
- 能够用在其他相关领域(SSA 重建/翻译命令式程序到 CPS)
SSA 构建
基本块分类
- filled:已经生成了基本块内的所有指令,只能再填入 phi 指令;
- sealed:已经遍历了基本块的所有前驱,不能再添加新指令。
因为只有在遍历完基本块内的所有指令才能访问其后继,因此所有 sealed 基本块一定是 filled。
插入 phi 结点
算法会在每个基本块中保存一份变量的“版本”(记录在 varDefs 中),并且可以通过 writeVar 和 readVar 两个方法进行获取。
如果当前基本块没有保存这个变量,则需要递归访问该基本块的所有前驱寻找其定义。
\begin{algorithm} \caption{Local Value Numbering} \begin{algorithmic} \procedure{WriteVar}{$var, bb, value$} \state $bb.curDef[var] \gets value$ \endprocedure \state \procedure{ReadVar}{$var, bb$} \if {$bb.curDef$ contains $var$} \return $bb.curDef[var]$ \endif \return \call{ReadVarRec}{var, bb} \endprocedure \end{algorithmic} \end{algorithm}
如果有多个前驱基本块,那么需要读取所有基本块的值并用 phi 结点汇聚。
但是向前驱结点递归寻找定义时会遇到环的问题。因此在基本块有多个前驱时,算法会预先插入一个空的 phi 函数并写入定义,然后再向前驱结点进行查找。这样在出现环形时,这个基本块会直接返回这个空的 phi 定义以打破环形的查找。
因此递归查找变量的过程分为三种情况:
- 当前基本块 unsealed:说明当前基本块的前驱还没有完成,应当先插入一个 phi 当作结果(当转为 sealed 时再化简当前指令及其 users)
- 当前基本块只有一个前驱:直接读取其结果
- 当前基本块有多个前驱:读取所有前驱的结果并生成 phi
\begin{algorithm} \caption{Global Value Numbering} \begin{algorithmic} \procedure{ReadVarRec}{$var, bb$} \if {$bb$ is not $sealed$} \state $value \gets$ new $\phi$ in $bb$ \state $bb.incompletePhis.add((var, value))$ \elseif {|bb.preds| = 1} \state $value \gets$ \call{ReadVar}{$var, block.preds[0]$} \else \state $value \gets$ new $\phi$ in $bb$ \state \call{WriteVar}{$var, bb, value$} \state $value \gets$ \call{AddPhiOp}{$var, value$} \endif \state \call{WriteVar}{$var, bb, value$} \return $value$ \endprocedure \state \procedure{AddPhiOp}{$var, phi$} \for{$pred \in phi.bb.preds$} \state add \call{ReadVar}{$var, pred$} as an operand to $phi$ \endfor \return \call{TryRemoveTrivialPhi}{$phi$} \endprocedure \end{algorithmic} \end{algorithm}
化简 trivial phi 结点
当然,这样得到的 phi 可能是 trivial 的。Trivial phi 的定义如下:
\[ \text{$\phi’$ is trivial} \Leftrightarrow \phi’ : \phi(x_1, x_2, \dots, x_n), x_i \in \{v, x\}, x \in V \]
在这样的 phi 结点中,v 表明值不变,因此其值一定为 x,所以可以直接化简为一个 x。
如果一个 phi 结点只引用了自己,说明这个基本块可能是一个不可达的基本块或者函数入口。对于前一种可以不用处理,对于后一种情况这个变量没有初值就直接使用了,因此此时可以直接返回 undef。
此时需要借助 tryRemoveTrivialPhi 进行化简。
\begin{algorithm} \caption{Detect and recursively remove trivial $\phi$ nodes} \begin{algorithmic} \state \comment{$v: \phi(x, x, …, v, v, …) \rightarrow x$} \state \comment{$v: \phi(v, v, …) \rightarrow undef$} \procedure{TryRemoveTrivialPhi}{$phi$} \state $same \gets $ empty \for {$op \in $ operands of $phi$} \if {$op = same$ \or $op = phi$} \continue \endif \if {$same$ is not empty} \state \comment{$phi$ merges at least two values, not trivial} \return $phi$ \endif \state $same \gets op$ \endfor \if {$same$ is empty} \state \comment{$phi$ has no operands} \return $undef$ \endif \state \comment{Remember all users except itself} \state $users \gets $ users of $phi$ except $phi$ \state replace $phi$ by $same$ \for {$use \in users$} \if {$use$ is a $\phi$} \state \call{TryRemoveTrivialPhi}{use} \endif \endfor \endprocedure \end{algorithmic} \end{algorithm}
封闭基本块
Unsealed 基本块主要出现在循环中,因为循环结构会出现环形,而当构建循环头时,循环体到循环头的后向边还没有构建。对于 unsealed 基本块而言,它不能向前驱基本块查找变量的定义。因此当后续基本块在 unsealed 基本块内找定义时,需要先插入一个 incomplete phi 结点进行占位并提前返回。当 unsealed 基本块变成 sealed 时,可以把先前的 phi 函数进行补充。
\begin{algorithm} \caption{Handling incomplete CFGs} \begin{algorithmic} \procedure{SealBlock}{$bb$} \for {$(var, value) \in bb.incompletePhis$} \state \call{AddPhiOp}{$var, value$} \endfor \state set $bb$ sealed \endprocedure \end{algorithmic} \end{algorithm}
对于不同的程序结构,其 filling 和 sealing 的过程也不同。但是都遵循其定义:
- 如果一个基本块内除 phi 结点外的指令都构建好了,那么它就是 filled
- 如果一个基本块的前驱都是 filled,那么它就是 sealed
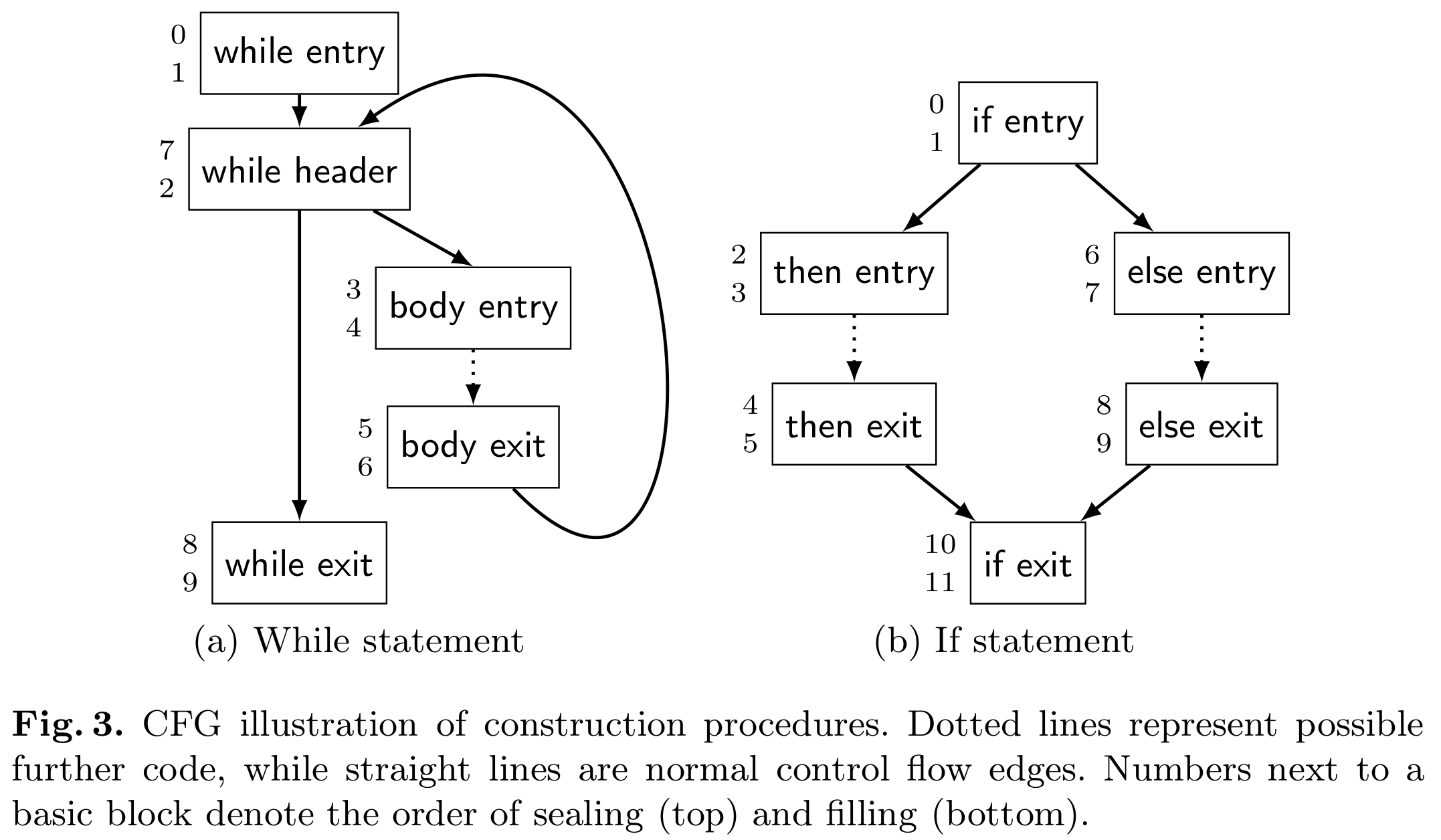
Figure 1: The process of filling and sealing for while and if statement
\(\phi-\text{SCC}\) 的定义和优化
冗余 phi 集合定义
原始代码中包含 goto 语句或者进行 on-the-fly 的优化后,算法可能会生成不可规约图。此时图中可能包含一些冗余的 phi 结点,其定义如下:
\[ \text{$\phi$ functions set $P$ is redundant} \Leftrightarrow \forall \phi_i \in P, \phi_i : \phi(x_1, x_2, \dots, x_n), x_i \in P \cup \{x\}, x \in V \]
当 \(|P| = 1\) 时,\(P\) 中的唯一 phi 结点即为前面定义的 trivial phi。
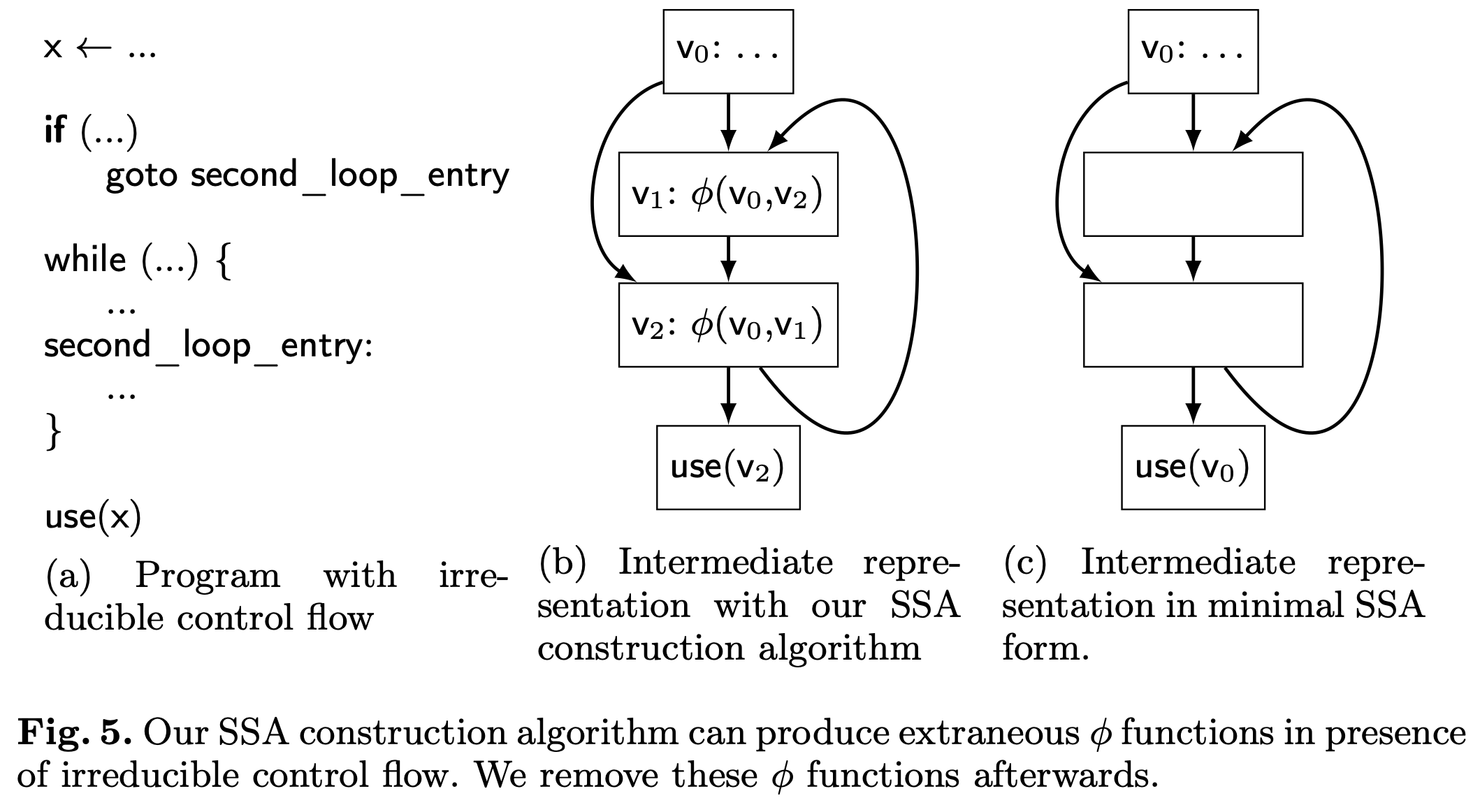
Figure 2: Irreducible control flow
冗余 phi 结点集合 \(P\) 中一定包含一个冗余的强连通分量(SCC)集合 \(S\)
对集合 \(P\) 形成的引用图进行缩点,得到有向无环图 \(P’\)。
设 \(P\) 引用的非 phi 结点为 \(x\)。对于 \(P’\) 上引用 \(x\) 的点 \(S\):
- 如果 \(|S| = 1\),则 \(S\) 中的 phi 结点为 trivial 结点,可化简;
- 否则 \(|S| > 1\),即 \(S\) 是一个 SCC,且是冗余的 phi 结点集合。
通过 phi-SCC 可以得到 minimal SSA 的另一种定义(是 cytron1991 中定义的增强形式,在算法性质中会证明):
(Minimal SSA (by \(\phi-\text{SCC}\))) 不包含 \(\phi-\text{SCC}\) 的程序为 minimal SSA。
化简算法
通过下面的算法可以消除程序中的 \(\phi-\text{SCC}\)。
\begin{algorithm} \caption{Remove $\phi-\text{SCC}$} \begin{algorithmic} \procedure{RemoveRedundantPhis}{$phis$} \state $sccs \gets$ \call{ComputeSCCs}{$phis$} \state \comment{Ensure used values outside scc are contracted} \for {$scc \in sccs.topologicalSort()$} \state \call{ProcessSCC}{$scc$} \endfor \endprocedure \state \procedure{ProcessSCC}{$scc$} \state \comment{The single node is processed by tryRemoveTrivialPhi} \if {$|scc| = 1$} \return \endif
\state \comment{$innerPhis$ consists of phis that only reference phis inner scc}
\state \comment{$outerOps$ consists of values that are not in scc}
\state $innerPhis \gets \emptyset$
\state $outerOps \gets \emptyset$
\for {$phi \in scc$}
\state $isInner \gets$ \TRUE
\for {$op \in$ operands of $phi$}
\if {$scc$ not contains op}
\state $isInner \gets$ \FALSE
\state add $op$ to $outerOps$
\endif
\endfor
\if {$isInner = $ \TRUE}
\state add $phi$ to $innerPhis$
\endif
\endfor
\if {$|outerOps| = 1$}
\state \comment{replace all phis in scc with the only outer op}
\state replace $scc$ by $outerOps[0]$
\elseif {$|outerOps| > 1$}
\state \comment{Reference more than one value, process $innerPhis$ recursively}
\state \call{RemoveRedundantPhis}{$innerPhis$}
\endif
\state \comment{else: the scc is unreachable, do nothing}
\endprocedure
\end{algorithmic} \end{algorithm}
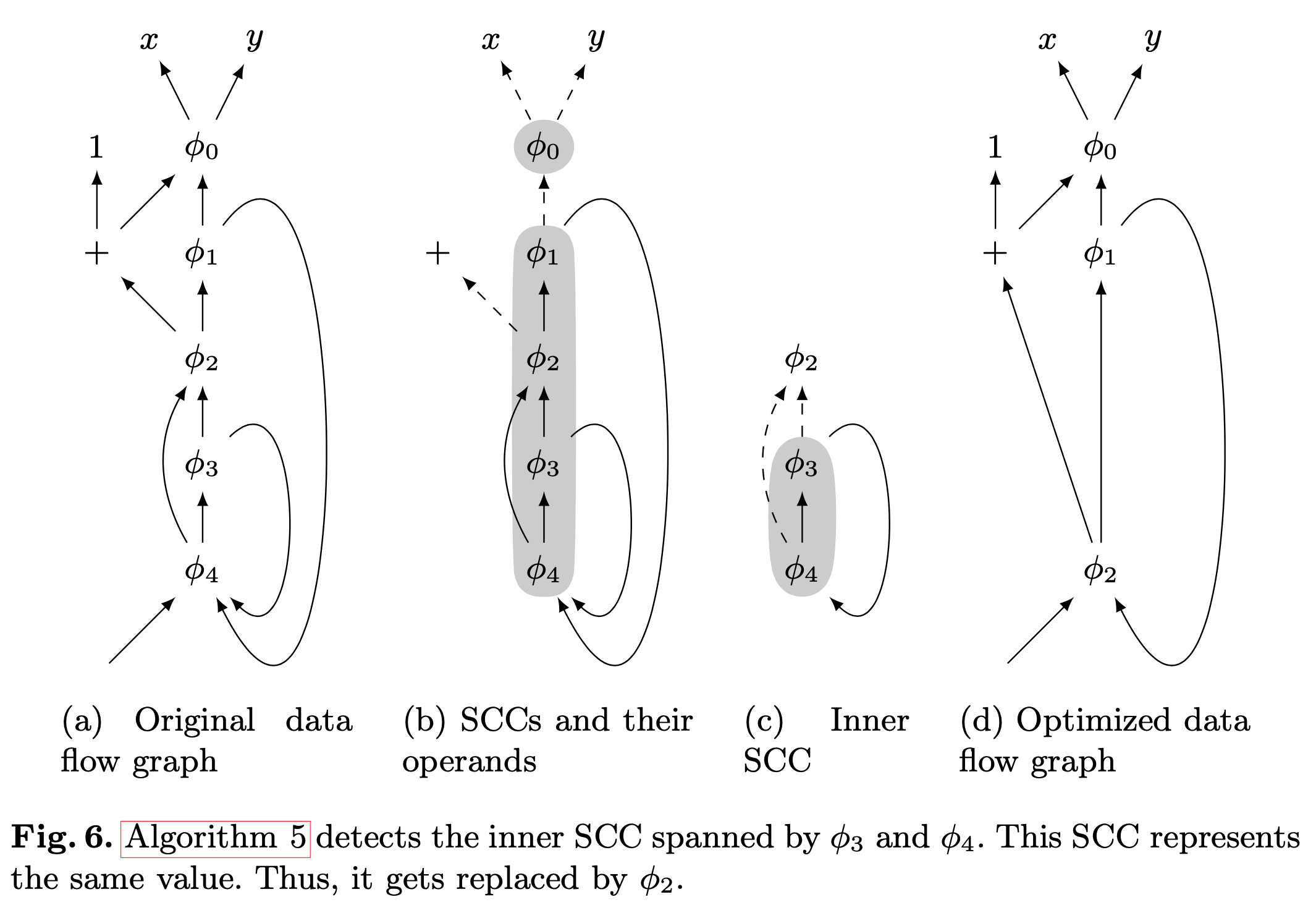
Figure 3: Remove redundant phis
算法性质
SSA 性质
(Pruned SSA Form) 所有的 phi 结点所对应的变量在该基本块入口都是活跃的。即 phi 结点至少有一个非自身的 user。
(Minimal SSA Form) 只在一个变量的两个不同定义交汇处插入 phi 函数。
Pruned SSA Form 的证明
由于本算法仅在需要的时候才插入 phi 结点,即所有的 phi 结点所在处其对应的变量都有 user,因此显然本算法可以构建 pruned SSA。
Minimal SSA Form 的证明
(路径汇聚) 称两条非空路径 \(X_0 \rightarrow^{+} X_J\) 和 \(Y_0 \rightarrow^{+} Y_K\) 汇聚于 \(Z\) 当且仅当以下性质满足:
- \(X_0 \ne Y_0\)
- \(X_J = Z = Y_K\)
- \((X_j = Y_k) \Rightarrow (j = J \vee k = K)\)
(Necessary phi 结点) 称基本块 \(Z\) 中的变量 \(v\) 对应的 phi 结点是必要的当且仅当存在两条非空路径 \(X \rightarrow^{+} Z\) 和 \(Y \rightarrow^{+} Z\) 汇聚于 \(Z\) 且 \(X\) 和 \(Y\) 中均包含 \(v\) 的定义。
只包含 necessary phi 结点的程序才是 minimal SSA。
(Reducible CFG) CFG \(G\) 是 reducible 的当且仅当对于 \(G\) 中的所有环 \(C\) 都存在环上结点 \(C\) 支配环内所有结点。
(SSA 性质) 在 SSA 形式中,变量 \(v\) 的某个定义到其使用的路径上不能包含 \(v\) 的令一个定义或 phi 结点,且phi 结点的参数的使用都在参数对应的前驱基本块上。
令 \(p\) 为 \(P\) 中的 phi 结点,\(q, r\) 都是 \(p\) 的参数且分别为 \(Q, R\) 中的定义。\(p, q, r\) 两两不同,则至少 \(Q, R\) 其中之一不支配 \(P\)。
设 \(p, q, r\) 是变量 \(v\) 的定义。假设 \(Q, R\) 均支配 \(P\),根据支配树的定义可知 \(Q, R\) 间存在支配关系。不妨设 \(Q\) 支配 \(R\),那么存在一条 \(Q \rightarrow^{+} R \rightarrow^{+} P\) 的路径,即定义 \(q\) 到 user \(p\) 的路径中存在 \(R\),且 \(R\) 重定义了 \(v\),矛盾。
如果基本块 \(P\) 内的 phi 结点 \(p\) 是 unnecessary but non-trivial 的,那么它的某个参数 \(q\) 是一个 unnecessary phi 结点且其基本块 \(Q\) 不支配 \(P\)。
设 \(p\) 是变量 \(v\) 的 phi 函数。由于 \(p\) 是 non-trivial 的,因此其至少有两个非自身的不同参数 \(r, s\),设其对应的基本块为 \(R, S\)。 \(r, s\) 有三种情况:
- \(v\) 的直接定义
- 一个 necessary phi 结点 \(r’\),此时存在两条非空路径汇聚于 \(R’\),因此也存在两条非空路径汇聚于 \(P\),矛盾
- 一个 unnecessary phi 结点
如果两个参数都是 \(v\) 的直接定义,那么 \(p\) 是 necessary phi 结点,矛盾。因此必定存在 unnecessary phi 结点。
不妨设 \(r\) 是 unnecessary phi 结点。假设 \(R\) 支配 \(P\),根据上一个 lemma 知,\(S\) 不支配 \(P\)。
由 \(r \ne p\),知 \(R \ne P\),因此 \(R\) 严格支配 \(P\),即 \(R\) 支配 \(P\) 的所有前驱。设 \(P\) 的某个前驱 \(S’\) 中 \(s\) 活跃,由 SSA 知存在不包含 \(R\) 的非空路径 \(S \rightarrow^{+} S’\)。又由于 \(R\) 支配 \(S’\),则 \(R\) 支配 \(S\)。
假设 \(s\) 是 necessary phi 结点,则存在两条包含 \(v\) 的定义的非空路径 \(Y_1 \rightarrow^{+} S\) 和 \(Y_2 \rightarrow^{+} S\) 汇聚于 \(S\)。令 \(X\) 是包含入口基本块到 \(R\) 最近定义的基本块。由于 \(R\) 支配 \(S\),则存在两条非空路径 \(X \rightarrow^{+} P\) 和 \(Y_1 \rightarrow^{+} P\),因此 \(p\) 是 necessary phi 结点,矛盾。
所以上面两个假设必然有一个不成立,即命题得证。
算法执行过程中,每次 phi 结点被创建或更新都紧跟一次 tryRemoveTrivialPhi,因此最终程序内不存在 trivial phi 结点。
不包含 trivial phi 结点的 reducible CFG 必然是 minimal SSA form。
假设 \(G\) 不包含 trivial phi 结点且 \(G\) 非 minimal SSA form。取其中一个 non-trivial and unnecessary phi 结点,则它有一个参数 \(q\) 是 unnecessary phi 结点且 \(Q\) 不支配 \(P\),那么同样 \(q\) 也有一个 unnecessary phi 结点。以此类推,由于程序中的 phi 结点数量是有限的,那么比如存在一个 phi 结点的引用环,此时 CFG 上必定也存在对应的环。
由于 \(G\) 是 reducible 的,因此存在环上结点 \(C\) 支配这个环。设 \(C\) 中的 unnecessary phi 结点被 \(D\) 引用,则 \(C\) 不支配 \(D\),矛盾。
因此 \(G\) 必然是 necessary phi 结点。
由于 \(\phi-\text{SCC}\) 的定义包含了 trivial phi 结点,因此不含 \(\phi-\text{SCC}\) 的程序一定是 minimal SSA form。
优化
对 triviality check 的优化
在算法运行过程中,会进行大量的 triviality 检查。为了加速这一部分,对于每个 phi 结点可以设置两个 witness,分别为其参数列表中头两个不相同的参数。
这样在进行 triviality check 时,只需要对比这两个 witness 是否相同。如果相同了,那么通过以下操作更新 witness:
\begin{algorithm} \caption{Optimization for triviality check} \begin{algorithmic} \procedure{TrivialityCheck}{$phi$} \if {witnesses of $phi$ is not initialized} \state \comment{initialize witnesses for $phi$} \state $wit_{1} \gets$ the first operand $op$ where $op \ne phi$ \state $wit_{2} \gets$ the first operand $op$ after $wit_{1}$ where $op \ne phi$ \and $op \ne wit_{1}$ \else \state \comment{update witnesses of $\phi$} \if {$wit_{1} = phi$ \or $wit_{1} = wit_{2}$} \state $wit_{1} \gets$ the first operand $op$ after $wit_{2}$ where $op \ne phi$ \and $op \ne wit_{2}$ \endif \if {$wit_{2} = phi$ \or $wit_{1} = wit_{2}$} \state $wit_{2} \gets$ the first operand $op$ after $wit_{2}$ where $op \ne phi$ \and $op \ne wit_{2}$ \endif \endif \if {$wit_{1}$ or $wit_{2}$ is empty} \return \FALSE \endif \endprocedure \end{algorithmic} \end{algorithm}
这样一来对于每个 phi 的检查次数从 \(\Theta(n^2)\) 化简到了 \(\Theta(n)\)。
构建时优化
此算法可以结合 GVN,运算强度削弱,复写传播,常量折叠等优化,在构建 SSA 时进行实时优化。
避免生成临时 phi 结点:标记优化
在访问前驱结点获取变量定义时,会调用 readVarRec 并创建临时的 phi 结点。但是在有项无环图中,这样生成的临时 phi 结点会在 tryRemoveTrivialPhi 中被删除。
为了避免生成大量的临时 phi 结点,可以通过一个 visited 标记表示当前结点被访问过,而不是直接插入 phi 结点。如果在递归过程中访问到了一个 visited 为真的结点,说明在一个环中,此处应当插入一个 phi 结点。
当所有前驱结点被访问后,再考虑移除 visited 标记,并根据 readVar 的结果插入 phi 结点。
避免生成临时 \(\phi-\text{SCC}\)
在递归放置 phi 结点的同时使用 Tarjan 算法检测 SCC。
如果 SCC 只引用了一个外界值,那么这个 SCC 可以直接用该值代替 phi 结点。
如果引用了多个外界值,则在每个引用外界值的基本块上放一个 phi 结点,然后在上面递归为其添加参数。在这个过程中会用类似 processSCC 的算法递归放置更多的 phi 结点。
时间复杂度
- \(B\) 为基本块数量
- \(E\) 为 CFG 边数
- \(P\) 为程序的大小
- \(V\) 为变量数量
只考虑 SSA 构建,则算法复杂度为 \(\Theta(P + (B + E) V)\);考虑对 SCC 的优化,算法的总复杂度为 \(O(P + B(B+E)V^2)\)。